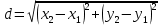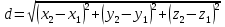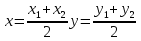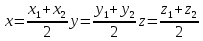Конспект урока «Декартовы координаты в пространстве. Координаты вектора» по математике
Тема урока: «Декартовы координаты в пространстве. Координаты вектора»
Цели урока:
1) Образовательная: напомнить учащимся, как задается прямоугольная система координат на плоскости, познакомить с декартовыми координатами, заданными в пространстве; углубить знания по изученной теме; формировать умения использовать полученные знания при решении нестандартных задач.
2)Развивающая: развивать познавательный интерес, память, графические навыки, активизировать деятельность учащихся на уроке; развивать у них грамотное математическое мышление и культуру речи, умение формулировать свои мысли, пользоваться зрительной и слуховой видами памяти.
3)Воспитательная: воспитывать интерес к предмету, чувство коллективизма, здорового соперничества, прививать коммуникативные навыки при работе в группах; создать условия для реальной самооценки учащихся.
Тип урока: комбинированный.
Оборудование урока: доска, раздаточный материал (карточки с заданиями).
Ход урока.
1. Организационный момент.
Проверить готовность к уроку.
Сообщить цели урока.
-
Активизация знаний.
Фронтальный опрос:
-
Что называется прямоугольной системой координат на плоскости?
-
Кто впервые ввел это понятие?
-
Как задается точка на прямоугольной системе координат?
-
Как задаются точки лежащие на координатных прямых?
-
Построить следующие точки на прямоугольной системе координат и соединить их линией:
| (4; – 0,5), | (– 9; 11), | (– 3; 2), |
«Кит»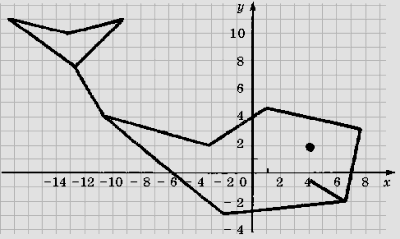
«Заяц»
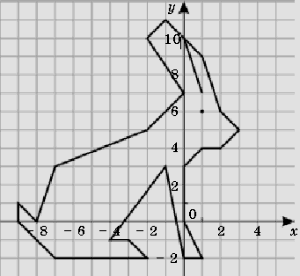
| (1; 7) | (– 2; 5) | (– 7; – 2) | (0; – 2) | (2; 4) |
-
Изучение нового материала.
В своё время Рене Декарт сказал: “… потомки будут благодарны мне не только за то, что я сказал, но и за то, что я не сказал и тем самым дал им возможность и удовольствие додуматься до этого самостоятельно”. Я предоставлю вам возможность и удовольствие разобраться с декартовой системой координат самостоятельно.
Предлагаю вам таблицу, которую мы с вами заполним, сделав сравнительную характеристику.
| В пространстве | |
| Определение. | Определение. |
| 2 оси, ОУ- ось ординат, ОХ- ось абсцисс | 3 оси, ОХ - ось абсцисс, ОУ – ось ординат, ОZ - ось аппликат. |
| ОХ перпендикулярна ОУ
| ОХ перпендикулярна ОУ, ОХ перпендикулярна ОZ , ОУ перпендикулярна ОZ. |
| (О;О) | (О;О;О) |
| (Х; У) | (Х; У; Z) |
| Расстояние между точками.
| Расстояние между точками.
|
| Координаты середины отрезка.
| Координаты середины отрезка.
|
Вопросы для заполнения первой части таблицы.
1. Сформулируйте определение декартовой системы координат?
2. Попробуйте сформулировать определение декартовой системы координат в пространстве?
3. Назовите оси координат на плоскости? Назовите оси координат в пространстве? Название, какой оси мы не изучали? (Знакомство с новым словом “аппликата”)
4.Под каким углом располагаются оси координат друг к другу?
5. Назовите координату начала координат на плоскости (в пространстве)?
6. Как задается координата точки на плоскости и в пространстве?
7. По каким формулам находится расстояние между двумя точками на плоскости и в пространстве? (Координаты середины отрезка)
-
Закрепление пройденного материала
1. Заполните таблицу
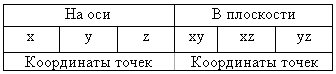
2. Задача. Постройте в системе координат точку N (-3;5;4).
Решение.
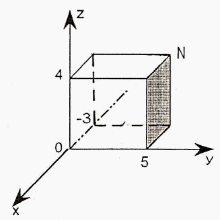 Постройте в системе координат точку М (-3;4;-2).
Постройте в системе координат точку М (-3;4;-2).
3. Найдите расстояние между А и В.
-
А(1,2,3) В(-1,0,5)
![]()
-
А(1,2,3) В(x,2,-3)
АВ=?
-
Итоги урока.
Запись домашнего задания. Выставление отметок.
д/з Задача. Вычислить координаты середины отрезка АВ, если А(2;-1;3) В(1,4,-1)
Здесь представлен конспект к уроку на тему «Декартовы координаты в пространстве. Координаты вектора», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.