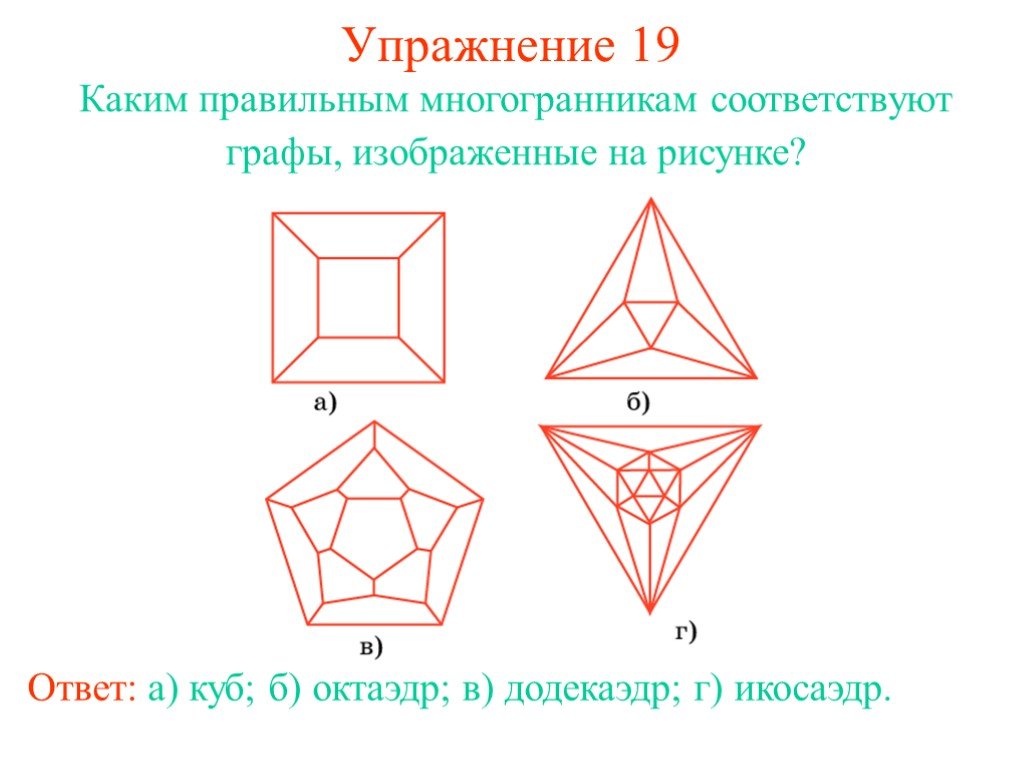
Презентация "Определение графа" по математике – проект, доклад
Презентацию на тему "Определение графа" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 28 слайд(ов).
Слайды презентации
Список похожих презентаций
Определение степени с натуральным показателем
«Веселые старты» среди 1-2 классов. «Веселые старты» среди 3-4 классы. Шахматы среди 5-х классов. Настольный теннис среди 6-7 классов. Баскетбол среди ...Определение производной
Производной функции y=f(x) называется предел отношения приращения функции к приращению независимого аргумента, когда приращение аргумента стремится ...Определение синуса, косинуса, тангенса и котангенса
Цели урока:. 1.Знать определение синуса, косинуса, тангенса и котангенса. 2.Уметь применять эти определения к решению примеров и задач. 3.Привитие ...Определение первообразной
Определение первообразной. Цели урока: Повторить правила дифференцирования; Ввести определение первообразной; Научить учащихся применять определение ...Определение подобных треугольников
Немного о себе. Привет всем меня зовут Алеся мне 15 лет учусь в №11 школе в 8 «Г» классе. Я занимаюсь в клубе самодеятельной песни. Мой клуб называется ...Определение арифметической прогрессии
. . ФОРМУЛА n-го члена арифметической прогрессии. . Устная работа № 16.1 № 16.2 № 16.3. . Информационные источники:. Мордкович А.Г., Семёнов П.В. ...Определение квадратного уравнения. Неполные квадратные уравнения
Решите уравнения Х=±2 Х=± Корней нет Х=0 Х=0,Х=2. 5х-2=0. Разделите данные уравнения на две группы. Какие уравнения называются квадратными? 1. Уравнение ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0. 1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...Определение двугранных углов
Открытый урок : «Двугранные углы» для учащихся 10-11 классов, изучающих геометрию по учебнику Л.С. Атанасяна. Автор : Дьяконова Надежда Сергеевна. ...Определение запыленности воздуха по листьям деревьев с использованием формулы Пика
Введение. В последние годы, наряду с изменениями климата, происходит значительное увеличение антропогенной нагрузки на природные и урбанизированные ...Определение гиперболы
Определение гиперболы. Геометрическое место точек плоскости, разность расстояний от которых до двух заданных точек F1, F2 есть величина постоянная, ...Определение геометрической прогрессии
ЦЕЛЬ УРОКА :. Формирование понятия геометрической прогрессии, используя сопоставление и противопоставления понятию арифметической прогрессии. Познакомить ...Определение вероятности
При классическом определении вероятность события определяется равенством Р(А) = m/n, где m – число элементарных исходов испытания, благоприятствующих ...Определение степени с натуральным показателем
Тема: Определение степени с натуральным показателем. Цели: • • Закрепить умение вычислять степень числа, умение выполнять вычисления, зная порядок ...Определение квадратного уравнения. Неполные квадратные уравнения
Тема урока: «Определение квадратного уравнения. Неполные квадратные уравнения» Цели урока: - познакомить учащихся с квадратными уравнениями в общем ...Определение угла
Класс: 7 «А» Дата: ноябрь 2010 года Предмет: геометрия Тип урока: объяснение нового материала Тема урока: «Первые уроки геометрии. Углы» Форма урока: ...Определение квадратного уравнения. Неполные квадратные уравнения
ax+b=0.1) (2х-3)2-2х(4+2х)=49, 2) y2+80=81, 3) -z+4=47, 4) 2x2+3х+1=0, 5) 4k/3+4=k/2+1, 6) 12s-4s2=0, 7) 10+p2-4p=2(5-3p), 8) 6(t-1)=9,4-1,7t, 9) ...
Понятие обратной функции. Определение логарифмической функции
Рассмотрим пример какой-либо функции, заданной в явном виде формулой y=f(x). Пусть, для определенности, это будет линейная функция y=2x–7. Вспомним, ...Определение квадратного уравнения. Неполные квадратные уравнения.
Эпиграф: Чтобы решить уравненье, Корни его отыскать, Нужно немного терпенья, Ручку, перо и тетрадь. Этапы подготовки:. Разбились на группы, которые ...Конспекты
Определение степени с натуральным показателем
Урок алгебры в 7 классе. . по теме «Определение степени с натуральным показателем». . в рамках проведения. . Всероссийского открытого урока ...Определение подобных треугольников
Урок по геометрии в 8 классе. «Определение подобных треугольников». Цель. 1. Ввести новые понятия: отношение отрезков, пропорциональные отрезки, ...Определение степени с натуральным показателем
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №13». муниципального образования г. Братска. ...Граф. Вершины и рёбра графа
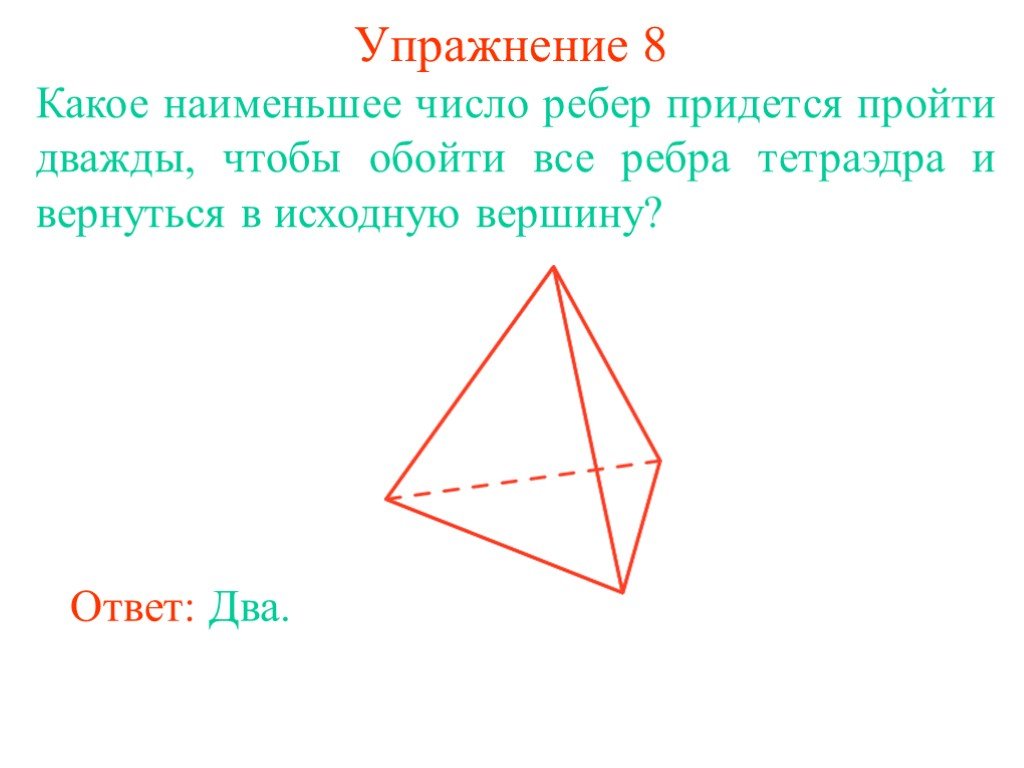
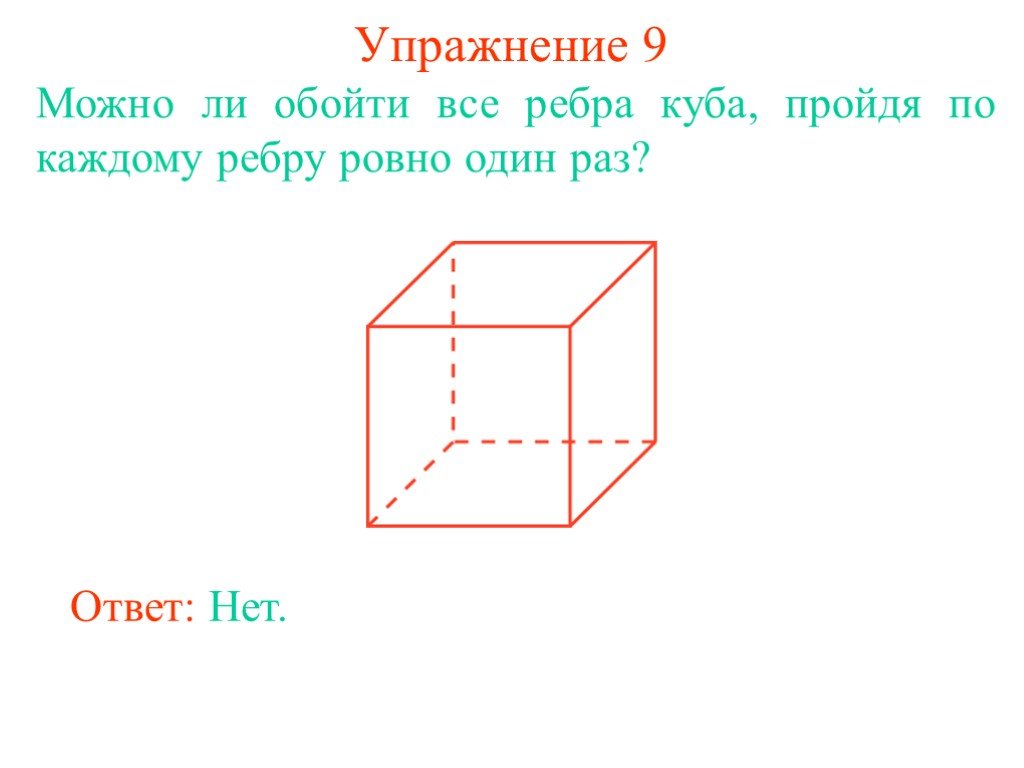
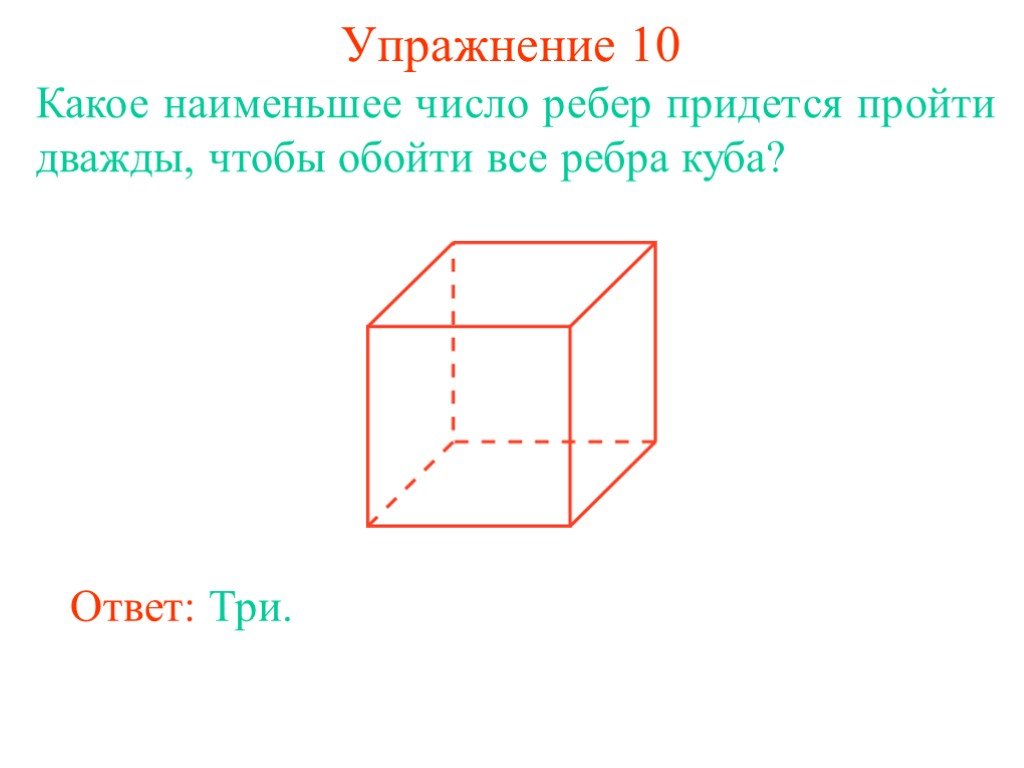
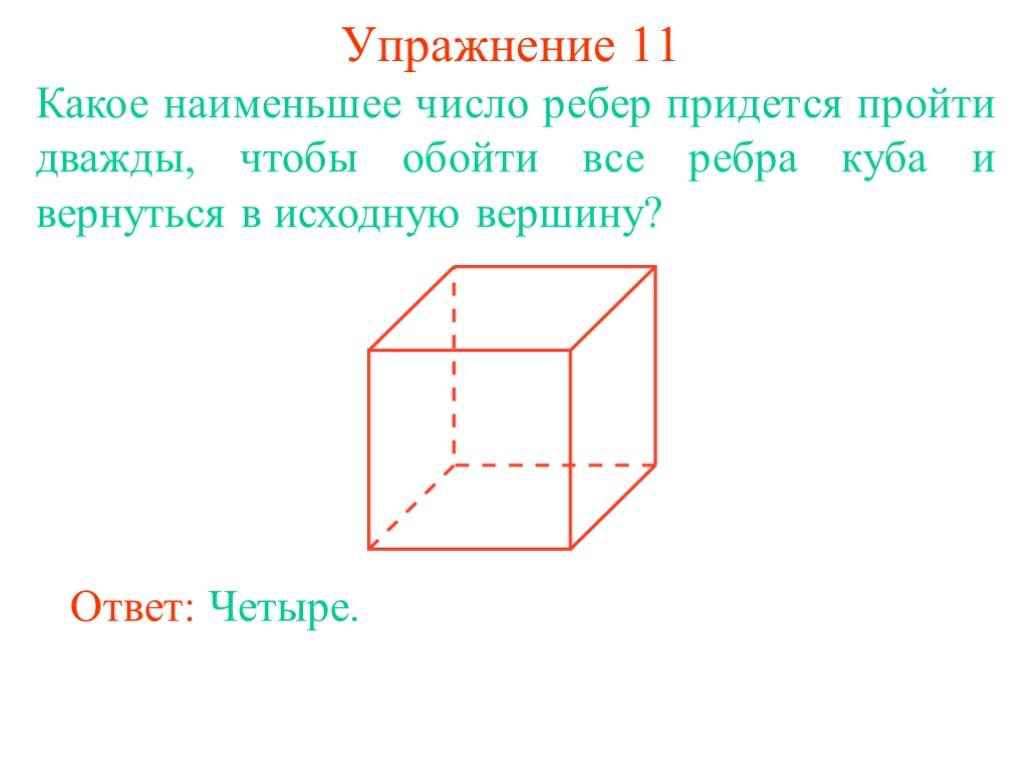
Класс: 3. Тема: Граф. Вершины и рёбра графа. Цель: Познакомить учащихся с понятиями «граф», «вершина», «ребра графа». Научить строить граф. Задачи:. ...Определение подобных треугольников
Леонова Людмила Михайловна. (. люда20. ). учитель математикиГБОУ лицей № 265 г. Санкт-Петербурга. Урок по геометрии в 8 классе по учебнику Л. ...Определение числа глагола. Изменение глаголов по числам
Русский язык (3-й класс). Тема: «Определение числа глагола. Изменение глаголов по числам». Учитель начальных классов:. ...Определение числовой функции. Область определения, область значений функции
Муниципальное общеобразовательное учреждение. Оковецкая средняя общеобразовательная школа. Селижаровский район Тверская область. Тема урока:. ...Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии
Тема урока:. «Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии». . Класс:9б. . Дата урока:10.02.2014. ...Определение квадратного уравнения. Неполные квадратные уравнения
План-конспект. урока по математике в 8 классе. «Определение квадратного уравнения. Неполные квадратные уравнения». Составила учитель ...Определение вероятности
Автор: Волобуева Лидия Ивановна. Место работы: РС(Я), Алданский район, МБОУ «Средняя общеобразовательная школа № 4 пос. Нижний Куранах». Тема: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:10 августа 2019
Категория:Математика
Содержит:28 слайд(ов)
Поделись с друзьями:
Скачать презентацию