Презентация "Неравенство треугольника" по математике – проект, доклад

Скачать презентацию (85.09 Кб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Презентацию на тему "Неравенство треугольника" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 6 слайд(ов).

Скачать презентацию (85.09 Кб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Неравенство треугольника

Автор: Малышев Виктор Евгеньевич , Муниципальное образовательное учреждение средняя общеобразовательная школа № 21, 7 «В» кл. Научный руководитель: Синцова Татьяна Витальевна, учитель математики МОУ СОШ № 21

Российская Федерация, Костромская область, городской округ город Шарья Школьный конкурс «Шаг в будущее»

Г. Шарья, 2009 год

Слайд 2

Цели: углубить и расширить знания по теме неравенство треугольников.

Задачи: разработать алгоритм решения задач; обучаться оформлению задач с использованием теоремы о неравенстве треугольников; научится решать задачи повышенной сложности.

Слайд 3

В треугольнике АВС сторона АВ больше стороны АС, отрезок AD - биссектриса. Докажите, что ∟ADB>∟ADC и BD>СD.

Дано: AB>AC, AD-биссектриса Доказать: ∟ADB>∟ADC,BD>CD Доказательство: 1)AC∟B, т.к. внешний ∟ACN=∟BKD, т.к. смежные с равными углами в ∆BKD ∟BKD>∟B, BD>KD, BD>DC

Слайд 4

Докажите что сумма длин диагоналей выпуклого пятиугольника меньше удвоенного периметра и больше полупериметра.

Дано: пятиугольник EDCBA Доказать: AC+BD+CE+DA+EB<2P AC+BD+CE+DA+EB>P/2 Доказательство: 1)ACP/2

Слайд 5

В целочисленном треугольнике (длины сторон которого являются целыми числами) длина одной из сторон равна 3, а периметр-18. Найдите длины двух других сторон треугольника.

Дано: произвольный треугольник, P=18 Решение: 1) а +в>3 a + в=15 в=15-a 2) a+ в>3 a+3> в в+3>a 3) a+15-a>3 a+3>15-a 15-a+3>a 4)15>3 2a>12, a>6 -2a>-18, a<9 5) a>6 a<9 Ответ:a=7,8

a=7,8

Слайд 6

Вывод:

В ходе создания проекта я расширил свои знания по теме неравенство треугольников, отработал навыки оформления задач и повысил технику решения задач повышенной сложности на неравенство треугольников.

Список похожих презентаций

Задачи на неравенство треугольника

Длина любой стороны треугольника не превосходит сумму длин двух других. | AC | ≤ | AB | + | BC |. Следствия из неравенства треугольника. Равенство ...

Соотношения между сторонами и углами прямоугольного треугольника

Найти: 1) sinA, 2) cоsA, 3) tg  A Ответ: sin A= Ответ: соsA= tg  A=. Дано: АВСD – трапеция, АВ = 16 см, ВАD = 30, СDА = 45. Найти: ВК и ...

Свойство биссектрисы равнобедренного треугольника

Повторение. Треугольник, у которого 2 стороны равны, называется равнобедренным треугольником. D С E B A C H M. DM – медиана треугольника АDВ. AM = ...

Свойства равнобедренного треугольника

Тема: «Свойства равнобедренного треугольника». Геометрия – это искусство хорошо рассуждать ... Нильс Г. Абель. Цели урока:. Создать условия для: введения ...

Вневписанная окружность треугольника

Вневписанная окружность. B A C Ka K1. Kb Kc ra rb rc. Определение. Вневписанной окружностью треугольника называется окружность, касающаяся одной из ...

Теорема Пифагора для треугольника

Теорема Пифагора. Легенды и факты о Пифагоре. Авторы презентации : Власенко Д., Белохвостова Т., Слизкова П., Матвеева П., Муравьева А. Пифагорейская ...

Сумма углов треугольника. Внешний угол треугольника

8 9 10 11 14 15 16 17 18 1 3 4 5 6 13 19 7. … по готовым чертежам. Теорема о сумме углов треугольника. А В С. Внешний угол треугольника. Свойство. ...

Сумма углов треугольника

«Вдохновение нужно в геометрии, как в поэзии» А.С. Пушкин. Математическая зарядка:. Сумма углов треугольника равна 180. Углы треугольника равны 180. ...

Геометрия в звездном небе. Свойство углов треугольника

Правила для членов клуба «ПИФАГОР»: Активно знакомиться с геометрическими терминами. 2. Радостно узнавать геометрические фигуры в повседневной жизни. ...

Высота треугольника

Все геометрические фигуры разделить на две группы. Назвать эти группы. Многоугольники. Немногоугольники. пятиугольник четырёхугольник треугольник ...

Внешний угол треугольника. Теорема о внешнем угле треугольника

I. Cумма углов треугольника. 1. На доске доказать теорему о сумме углов треугольника: Сумма углов треугольника равна 1800 2. Решить задачу № 749 (чёт ...

Внешний угол треугольника

Общий вид внешнего угла. Понятие. Свойство внешнего угла. Внешний угол. Внешний угол треугольника. Угол, смежный с каким–нибудь углом треугольника, ...

Внешний угол треугольника

Треугольник (музыкальный инструмент). Жесткость треугольников. Бермудский треугольник. ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА. У треугольника может быть два тупых ...

Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним

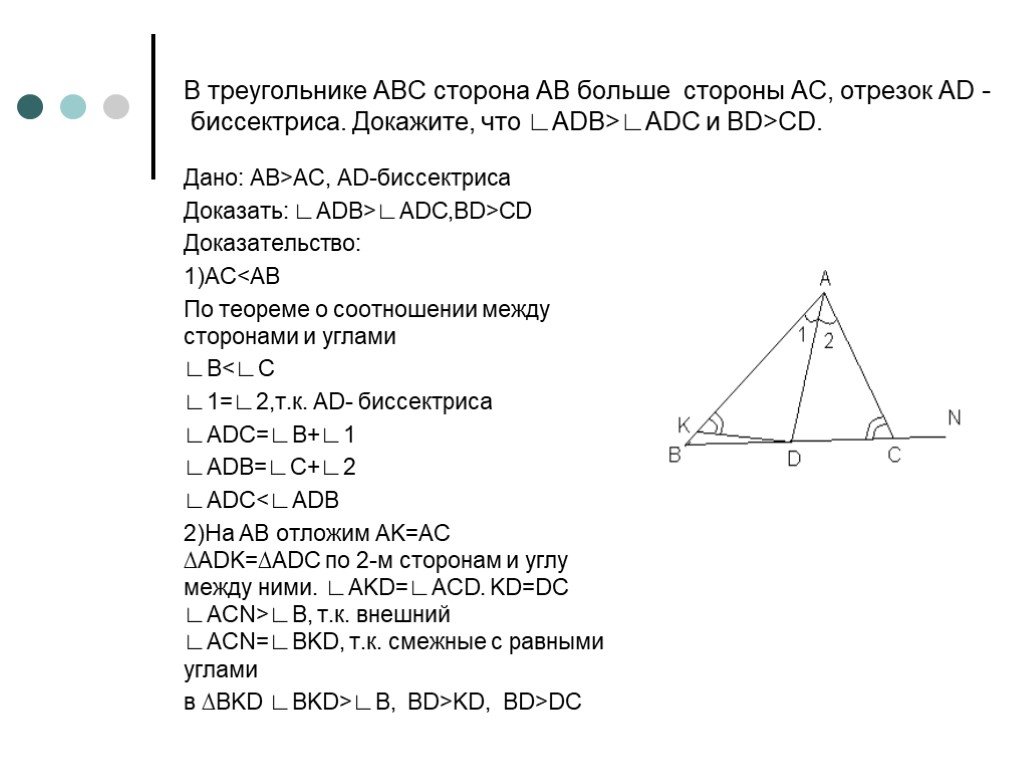
Теорема 2. В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны ...

Соотношения между сторонами и углами треугольника

Работаем устно ( теоретические сведения). А С В. 1. Назовите фигуру представленную на рисунке. 2. Перечислите названия её составных частей. 3. Укажите ...

Средняя линия треугольника

А В С D О. Диагонали четырёхугольника АВСD пересекаются в точке О, причём АО:ОС=ВО:ОD. Докажите, что АВСД –трапеция. Устно:. М N. Точка М– середина ...

Задачи на вычисление площади треугольника

Девиз урока: «Кто ищет – тот всегда найдет…». Личностные цели. самостоятельно добывать знания, анализировать и обобщать; уверенно и грамотно выражать ...

Сумма углов треугольника

Разминка. №1. Укажите внутренние накрест лежащие и внутренние односторонние углы при параллельных. = М А В Д С. №2. Определите, какие стороны у четырехугольника ...

История треугольника

Что такое треугольник? Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, ...

Теорема о пересечении высот треугольника

Цели:. 1) Рассмотреть теорему о точке пересечения высот и следствие из неё; 2) Формировать умения применять известные знания в незнакомой ситуации, ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.