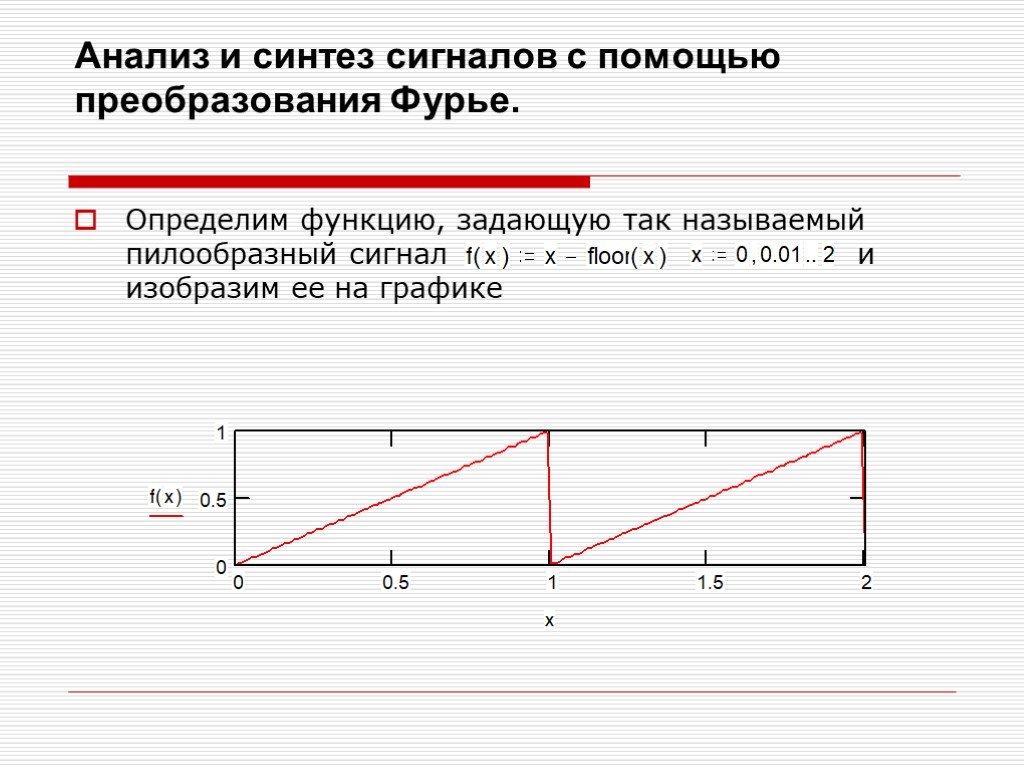
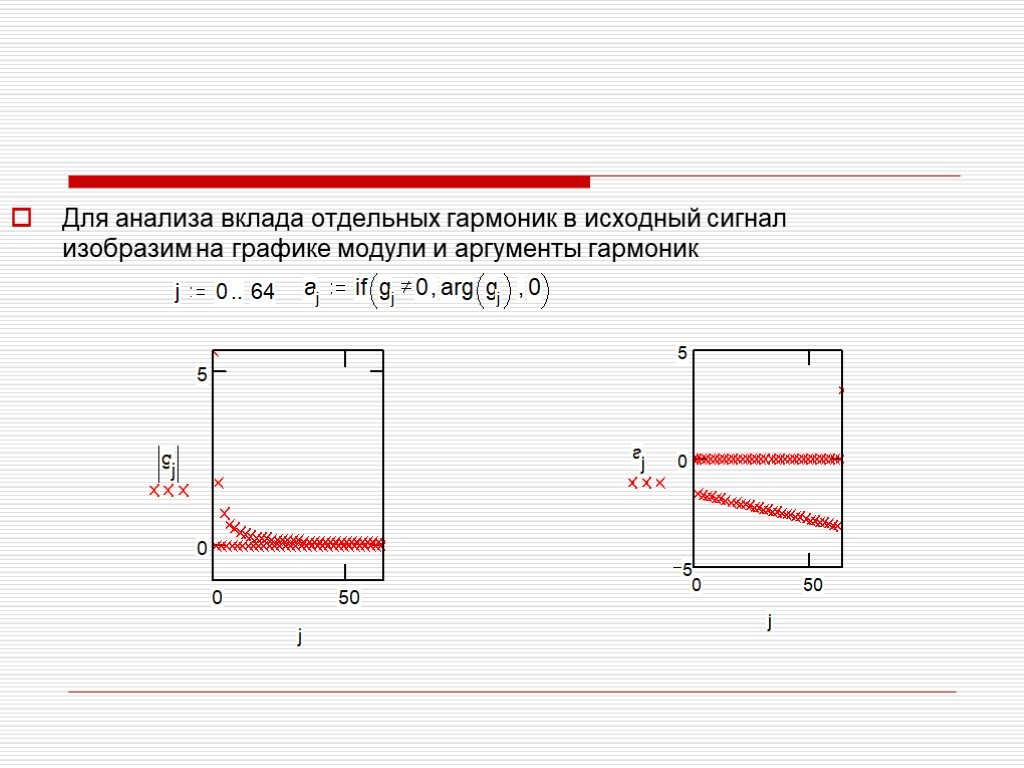
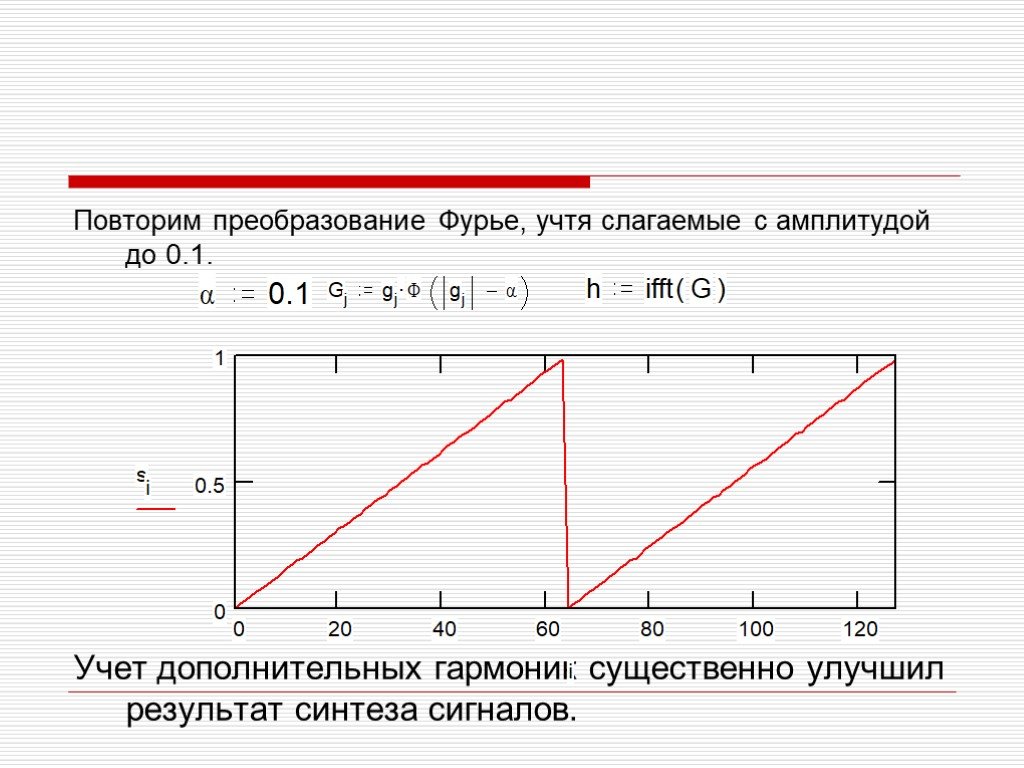
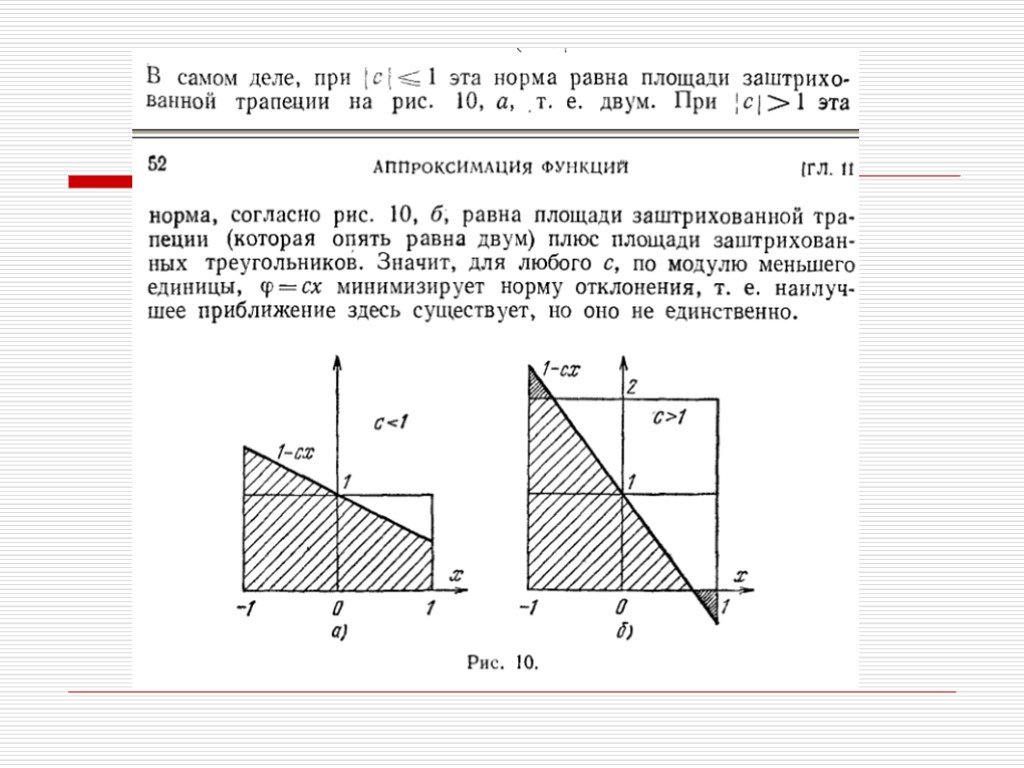
Презентация "Преобразование Фурье" по математике – проект, доклад

Скачать презентацию (0.59 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Презентацию на тему "Преобразование Фурье" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).

Скачать презентацию (0.59 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Преобразование Фурье

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Анализ и синтез сигналов с помощью преобразования Фурье.

Определим функцию, задающую так называемый пилообразный сигнал и изобразим ее на графике

Слайд 8

Заполним массив s: Проводим прямое преобразование Фурье: Внимание! В том случае, когда в массиве s содержится элементов, причем все числа действительные, следует использовать функцию fft. Во всех остальных случаях – функцию cfft. Массив g содержит комплексные коэффициенты дискретного преобразования Фурье. Размер массива f –

Слайд 9

Для анализа вклада отдельных гармоник в исходный сигнал изобразим на графике модули и аргументы гармоник

Слайд 10

Проводим обратное преобразование Фурье, исключив гармоники с малым вкладом. Будем учитывать только гармоники с амплитудой не менее 0.3. Для отсечения слагаемых с малым вкладом воспользуемся функцией единичного скачка – функцией Хевисайда Ф. Для обратного преобразования Фурье используется функция ifft, если прямое преобразование осуществлялось с помощью fft, и cifft, если прямое преобразование осуществлялось с помощью cfft.

Слайд 11

Слайд 12

Повторим преобразование Фурье, учтя слагаемые с амплитудой до 0.1. Учет дополнительных гармоник существенно улучшил результат синтеза сигналов.

Слайд 13

Наилучшее приближение

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Список похожих презентаций

Дискретное преобразование Фурье

Дискретное преобразование Фурье. Мысленно периодизируем этот сигнал с периодом Дискретный периодический сигнал можно представить рядом Фурье: Коэффициенты ...

Быстрое преобразование Фурье

Быстрое преобразование Фурье. Основной принцип всех этих алгоритмов заключается в разложении операций вычисления ДПФ сигнала длины на вычисление преобразований ...

Преобразование фигур на плоскости. Виды движения

Преобразование плоскости, при котором расстояние между двумя любыми точками сохраняется, называется движением. Из определения следует, что при движении ...

Преобразование целого выражения в многочлен

Старт. Первый этап Гонка. Что такое биатлон? Это зимний вид спорта, сочетающий лыжную гонку со стрельбой из винтовки. Первые официальные соревнования, ...

Преобразование Наполеоном многоугольников

Содержание: 1. Введение. 2. Преобразование Наполеона треугольников. а) Преобразование Наполеона вложенных фигур. б) Ядро линейного преобразования. ...

Преобразование тригонометрических выражений

Учебные элементы. Синус, косинус, тангенс суммы и разности аргументов. Формулы двойного аргумента.(теория, примеры, задания) Формулы понижения степени. ...

Преобразование графиков функций на координатной плоскости

Эпиграф к уроку. Красота в единстве теории и практики. Цели обучения, воспитания и развития. Рациональные способы построения графиков функций. Развитие ...

Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа.

1. У = - f(x) ← y = f(x) , симметрия относительно оси ОХ. 2. У = f(- x) ← y = f(x), симметрия относительно оси ОУ. 3. У = - f (- x) ← y = f(x), симметрия ...

Преобразование графиков функции

Повторение. Как построить график функции если известен график функции. . Рассмотрим построение графика функции. 1 случай: m – положительное число. ...

Знакомство с рядами Фурье

Определение ортогональной системы функций. Тригонометрическая система функций называется ортогональной на отрезке [-,] и на всяком отрезке длины ...

Преобразование выражений содержащих квадратные корни

Свойства арифметического квадратного корня. Квадратный корень из произведения и дроби. Квадратный корень из степени. При любом. Теорема 1 . ...

Преобразование выражений, содержащих квадратные корни

Устно. Вычислить:. . Устно. Решить уравнение:. x2=81 х = 9; -9 x2=0,36 х = 0,6; -0,6 x2=1 х = 1; -1. Устно. Выполнить действия, используя формулы ...

Преобразование выражений

Какие свойства действий позволяют без выполнения вычислений утверждать, что верно равенство:. Найдите значение выражения и укажите, какие свойства ...

Преобразование алгебраических выражений

Девиз урока:. Математику нельзя изучать, наблюдая как это делает сосед. План урока:. Сообщение темы урока. Рефлексия на начало урока Этап проверки ...

Понятие степени. Свойства степени. Преобразование степеней

Понятие степени с натуральным показателем. Свойства степени с натуральным показателем. Степень с целым и дробным показателем. Понятие корня. Преобразования ...

Преобразование целого выражения в многочлен

Проверка домашнего задания. №975 (а) (х3+7х2+8)+(х2-6х+4)(х-1)= =2х3+10х+4 №981 (в,г) в) 9а2-16ав г) 20х2+24ху №1067 (а(а+2в)+в2)(а(а-2в)+в2)((а2- ...

Преобразование графиков функций

Основные правила преобразования графиков функций. 1. У = - f(x) ← y = f(x) , отображением относительно оси ОХ. 2. У = f(- x) ← y = f(x), отображением ...

Преобразование выражений, содержащих квадратные корни

Фронтальный опрос. Дайте определение арифметического квадратного корня. Перечислите свойства арифметического квадратного корня. Чему равно значение ...

ЕГЭ В7. Преобразование логарифмических выражений

Номера заданий. №4329 №4351 №4367 №4385 №4415 №4435 №4505 №4525. 06.01.2018. №26857 №26858 №26860 №26862 №26882 №26883 №26889 №26892. №26894 №26896 ...

Преобразование графиков функций

Дорогу осилит идущий, а математику – мыслящий Т.Эдисон. Цель урока. Изучить способ построения графиков функций y = f(kx), y = mf(x). Преобразование: ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.