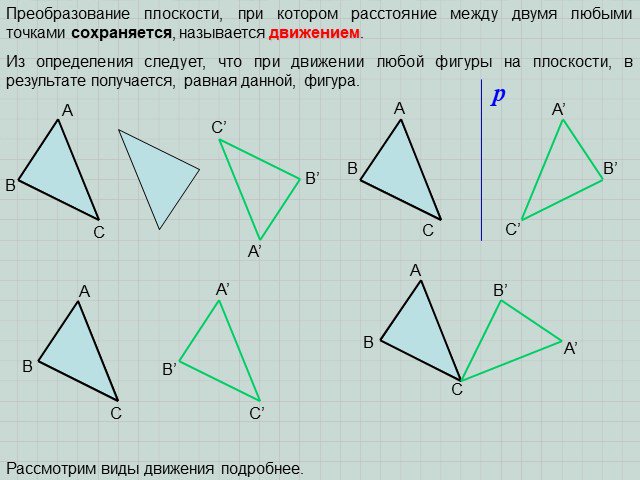
Презентация "Преобразование фигур на плоскости. Виды движения" по математике – проект, доклад
Презентацию на тему "Преобразование фигур на плоскости. Виды движения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
Слайды презентации
Список похожих презентаций
"Разрезание геометрических фигур на части"
ЗАДАЧИ НА РАЗРЕЗАНИЯ. Теорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат. ...Виды вкладов и расчет накоплений
Цель работы : развитие экономического образа мышления - умения применять аппарат математики и экономики для анализа конкретных экономических явлений ...Виды движения
Понятие движения. Движение пространства – это отображение пространства на себя, сохраняющее расстояния между точками. Примером движения могут служить: ...Виды. Количество видов на чертежах
Вид – это изображение обращенной к наблюдателю видимой части поверхности предмета. Определение:. . 1. Вид спереди – главный вид (размещается на месте ...Виды движения тел
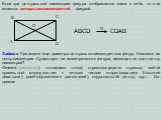
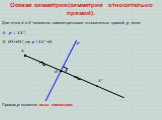
Теорема 2. Зеркальная симметрия является движением. Доказательство. Пусть точки A’, B’ получены симметрией относительно плоскости точек A, B, A”, ...Взаимное расположение прямых на плоскости
Цели:. Обобщить знания о прямых на плоскости из алгебры и геометрии 7 класса. Выяснить взаимное расположение прямых, заданных уравнением y=kx+b в ...Виды треугольников по сторонам
Листок настроения. В начале урока у первого человечка нарисовать свое настроение , в конце – у второго. Сегодня, друзья, Мы отправимся в путь. Хорошее ...Взаимное расположение прямой и окружности на плоскости
Прямая и окружность пересекаются. d R. d- расстояние от центра окружности до прямой R- радиус окружности. О А В d. Прямая и окружность касаются. d=R. ...Виды симметрии. Центральная и осевая симметрия
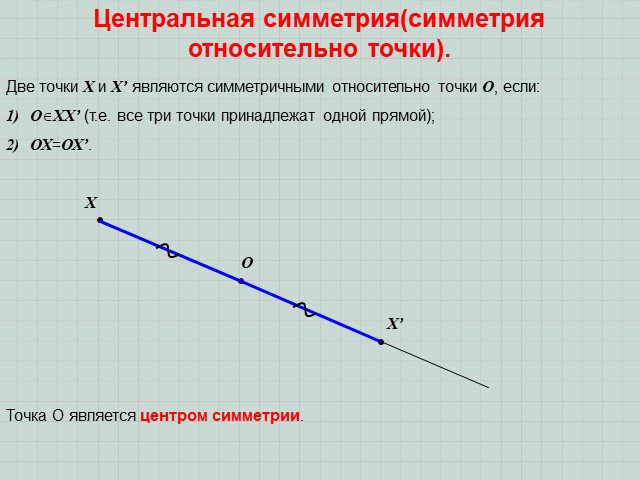
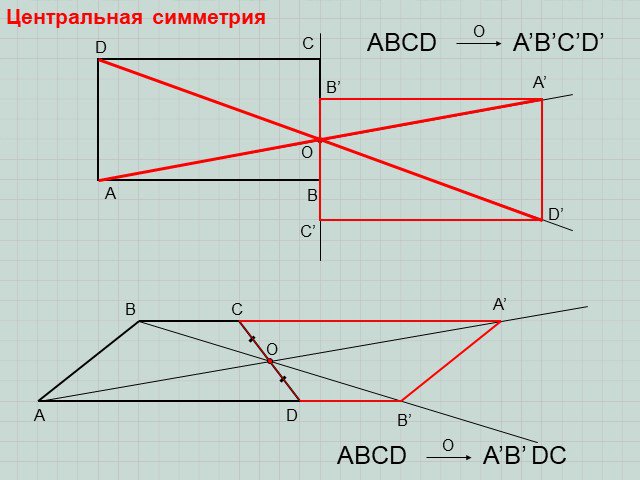
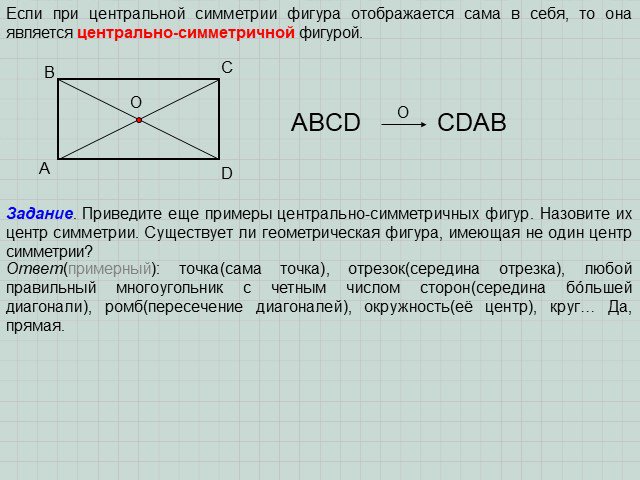
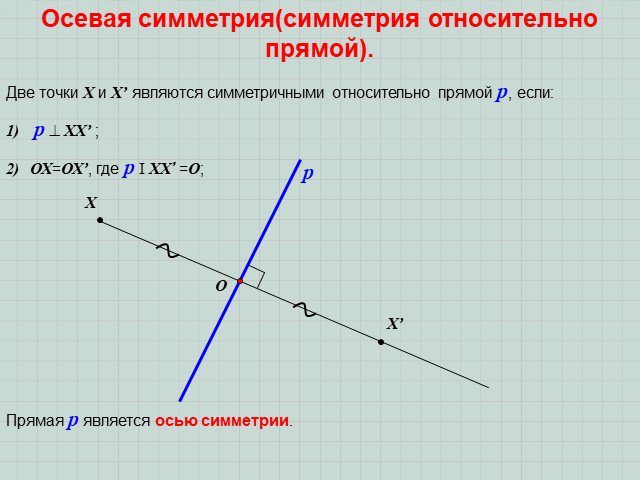
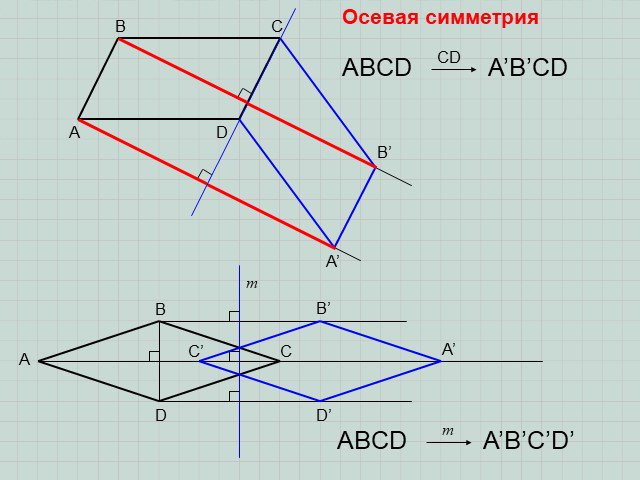
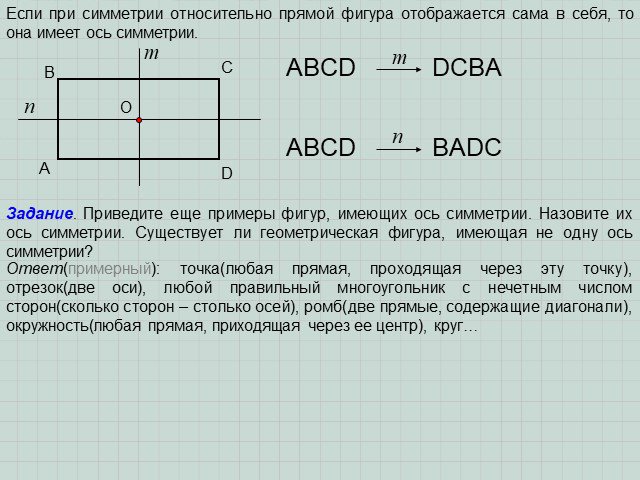
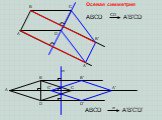
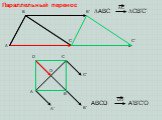
ОСЕВАЯ(ЗЕРКАЛЬНАЯ) СИММЕТРИЯ. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ. Что такое симметрия? Какие точки называются симметричными? Симметрия – это соразмерность, одинаковость ...Астрономия на координатной плоскости
Цели урока:. Закрепить полученные знания и навыки. Проявить творчество при изучении данного раздела. Избежать трудностей при изучении темы «Функция» ...Векторы на плоскости
Аналитическая геометрия. Алгебраические поверхности и линии на плоскости первого порядка. Опр. Геометрическое место точек в пространстве (на плоскости) ...Алгоритмы работы на координатной плоскости
Цели:. Формировать умение работать на координатной плоскости как с положительными, так и отрицательными координатами. Развивать алгоритмическое мышление. ...Аксиомы расположения точек на прямой и плоскости
Выполните действия и сделайте записи:. 1. Изобразите точку С, лежащую на прямой а. 2. Изобразите точку D, не лежащую на этой прямой. 3. Проведите ...Виды треугольников
ТРЕУГОЛЬНИКИ ОСТРОУГОЛЬНЫЕ ПРЯМОУГОЛЬНЫЕ ТУПОУГОЛЬНЫЕ. Треугольником называется фигура ,которая состоит из трёх точек , не лежащих на одной прямой, ...Авария на промышленном объекте
Цели урока:. Повторить материал по темам “ Площади криволинейных трапеций”, “Решение показательных уравнений”, выявить пробелы в знаниях и постараться ...Виды симметрии
Определение. В древности слово «симметрия» употреблялось как «гармония», «красота». Действительно, по-гречески оно означает «соразмерность, пропорциональность, ...Виды многогранников
Геометрия является самым могущественным средством для изощрения наших умственных способностей.Г.Галилей. Многогранником называется тело, ограниченное ...
Виды квадратных уравнений
гипотеза. Каждый человек, особенно если он ученик 8 класса, может решить квадратное уравнение, если знает ответы на вопросы…. вопросы... Определение ...«Задачи на проценты»
Тема урока: Проценты. Тип урока: урок обобщения и систематизации знаний. Цели урока: Образовательные: Обобщение и систематизация знаний учащихся о ...Виды четырёхугольников
Четырёхугольники невыпуклые выпуклые параллелограммы трапеции прямоугольники ромбы квадраты равнобедренные прямоугольные Проверь себя! Выпуклые многоугольники. ...Конспекты
Виды треугольников. Плоскостное моделирование и конструирование. Аппликация из геометрических фигур — треугольников
Тема. : «Виды треугольников. Плоскостное моделирование и конструирование. Аппликация из геометрических фигур — треугольников». . Цели занятия. ...Вычисление площадей фигур на клетчатой бумаге. Формула Пика
Урок геометрии в 8 классе по теме «Вычисление площадей фигур на клетчатой бумаге. Формула Пика.». (Методические рекомендации). Учитель. Берестова ...Астрономия на координатной плоскости
Леткова Татьяна Викторовна,. учитель математики. Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа ...Векторы на плоскости
. Конспект. обобщающего урока по теме «Векторы на плоскости». . (геометрия 9 класс). Тема. Систематизация и обобщение изученного материала ...Виды углов. Умножение и деление двузначного числа на однозначное
Павлодарская область. Актогайский район. . с.Барлыбай. . . Енбекшинская средняя школа. Тема:. . «Виды углов. Умножение и деление двузначного. ...Вычисление площадей фигур на клетчатой бумаге
Фрагмент урока по теме:. . Вычисление площадей фигур на клетчатой бумаге. . . Цель :. . c. истематизация знаний по нахождению площадей геометрических ...Время движения
Тема:. Время движения. Цель:. Ознакомить с нахождением времени. Развивать умение детей решать задачи и примеры. Воспитывать усидчивость и взаимопонимание. ...Вместе весело шагать на экзамен
КОУ ВО «ТАЛОВСКАЯ ШКОЛА-ИНТЕРНАТ ДЛЯ ДЕТЕЙ-СИРОТ И ДЕТЕЙ, ОСТАВШИХСЯ БЕЗ ПОПЕЧЕНИЯ РОДИТЕЛЕЙ». 9 КЛАСС. ПРИГОТОВИЛИ : Гриценко Р.А. Носова ...Виды углов в планиметрии
Лабораторно-практические занятия по геометрии в 7 классе. Лабораторно-практические занятия имеют важное значение, особенно при обучении детей с ...Виды углов
Мисуно Татьяна Владимировна. учитель начальных классов Аккайинской ОШ. первой категории. урок по математике в 4 классе. Тема. :. Виды углов. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:неизвестен
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию