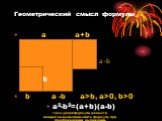
Презентация "Разность квадратов чисел" по математике – проект, доклад

Устно

Разложить на множители: а(m+n)+b(m+n) b(a+5)-c(a+5) 2m(m-n)+m-n 7(c-3)-a(3-c) 6(a-2)+(2-a) Какие способы разложения многочленов вы знаете?

тема урока:формула разности квадратов.Цель:применить формулу при преобразовании выражений.

Возведите в квадрат

3a; 0,2m; (1/3)x; (3/8)y3; 0,3y2 Представьте в виде квадрата одночлена: 9b2; 16m4; 0,09x10; 0,81m2n2; 4b2 тема урока:формула разности квадратов.Цель:применить формулу при преобразовании выражений.

Работа с таблицей (в парах)

1. 3m-2m 2. ax-ay 3. 9x2-16 4. 9a+3x2 5. m2-n2 6.8ax+16ay+3bx+6by

7. 9mn+9n 8. ac-3bd+ad-3bc 9. 25a2- 36b2 10. a2-9b2 11. 100x2-64y2 12. 2x(x+y)-3(x+y)

Заполните таблицу, поместив туда номера соответственных выражений.

Проверим, какие номера записали в столбики

ложитМММмнмножитемногочлены№1;2;6;7;12;3;5 С как назымваютсявыраженсномерам третьего столбика? Можете ли вы преобразовать эти выражения?

Можете ли преобразовать выражения в 3 столбике?

Тема урока:

Разность квадратов.

Цели урока:

Организовать деятельность учащихся на самостоятельный вывод формулы разности квадратов. Выработать умение распознавать формулу разности квадратов в различных ситуациях, выделять эту формулу из других выражений, применять ее при преобразовании выражений. Организовать учащихся на доброжелательное отношение друг к другу, на взаимопомощь и взаимовыручку.

Выполните умножение

1 группа 2 группа (2b+3)(2b-3) (a+b)(a-b) Как можно прочитать формулу? (a+b)(a-b)=a2-b2

(3x-2y)(3x+2y) (m-n)(m+n)

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений. Формулу (a+b)(a-b)=a2-b2 можно записать с помощью условных знаков (▲—)(▲+)=▲2—2 Эта формула называется формулой сокращенного умножения

Проверьте справедливость этой формулы при а=5; b=4; Сделайте вывод.

а и в могут быть любым числом или выражением Формула сокращенного умножения применяется для упрощения вычислений 63x57= (60+3)(60-3) 98x102= (100-2)(100+2)

(60+3)(60-3)=3600-9=3591 (100-2)(100+2)=1000-4=9996 Решить № 359

Формула (а+b)(a-b)=a2-b2 имеет геометрическую интерпретацию

Геометрический смысл формулы

а a+b b а -b a>b, a>0, b>0 a2-b2=(a+b)(a-b)

b a-b

Исследования:

Влияет ли порядок записи скобок на результат? (4m-3)(4m+3)= 16m2-12m+ 12m-9= 16m2-9 (4m+3)(4m-3)= 16m2- 12 m+ 12m-9= 16m2-9 Важен ли порядок записи слагаемых в одной из скобок? (4m-3)(3+4m)= 12 m +16m2-9 -12m = 16m2-9 ВЫВОД: порядок записи скобок и записи слагаемых роль не играют. ФИЗКУЛЬТМИНУТКА

Важен ли порядок записи уменьшаемого и вычитаемого в одной из скобок?

(3-4m)(3+4m)=9+12m-12m-16m2 = -16m2+9 Вывод: уменьшаемое и вычитаемое нельзя менять местами, получается совсем другое выражение. По какому множителю (а+b) или (а-b) нужно составлять результат? Я исследовал, что слагаемые можно поменять местами, а уменьшаемое и вычитаемое нельзя менять местами, значит, результат нужно составить по множителю (а-b).

Закрепление:

(5x-3y)(5x+3y)= (0,5m-0,2n)(0,5m+0,2n)= Самостоятельно: №356(1,3),351(1)-устно,2-у доски

Любую формулу в математике можно читать как слева направо, так и справа налево. Запишем эту формулу справа налево. a2-b2=(a+b)(a-b) Как можно прочитать формулу?

Разность квадратов двух выражений (чисел) равна произведению суммы этих выражений (чисел) на их разность. m2-n2=(m-n)(m+n)-формула разности квадратов. Запишем эту формулу с помощью условных знаков ▲2—2=(▲—)(▲+)

№352(1-учитель,3-ученик ), 353-самостоятельно по вариантам. №355(1,3),363(1,2,3,5)

Используя формулу разности квадратов преобразуйте выражения: a2-9b2 100x2-64y2 РЕШИТЬ

Итог урока

1. С какой новой формулой мы сегодня познакомились? 2. Что нового мы сегодня узнали? 3. С какими трудностями вы сегодня встретились? 4. На что следует обращать внимание при применении формулы (a+b)(a-b)=a2-b2

Домашнее задание

№351(3);352(2);355(2,4); 360;363(4,6)

Спасибо за урок