Презентация "Площади фигур" по математике – проект, доклад
Презентацию на тему "Площади фигур" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Площади фигур
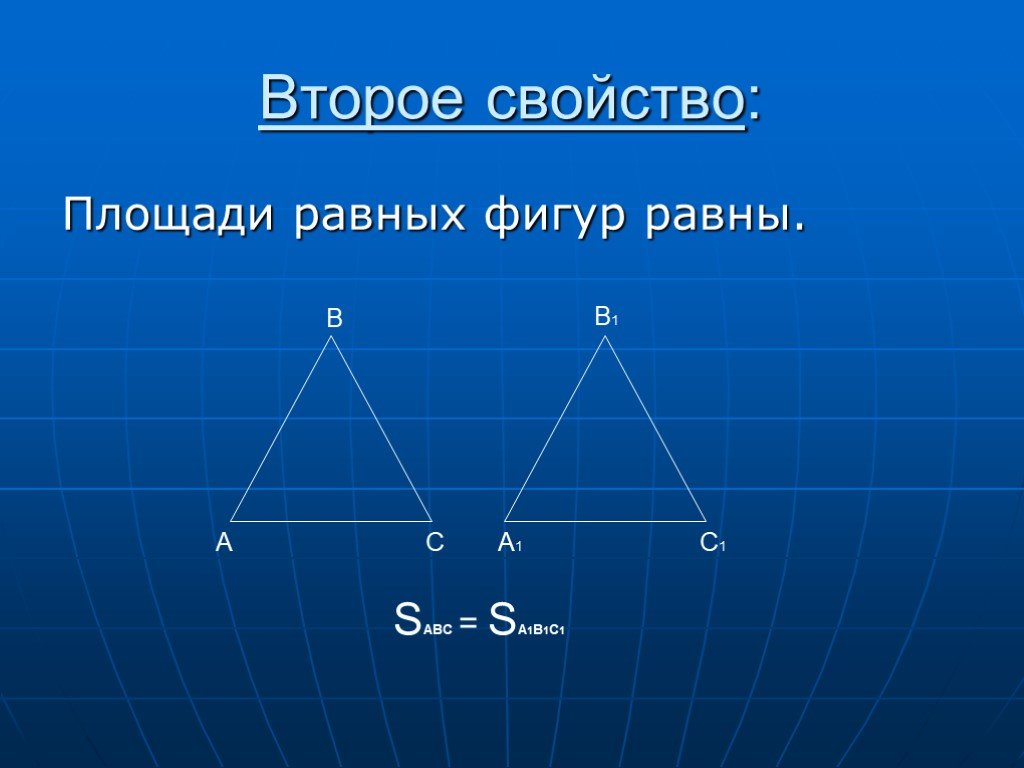
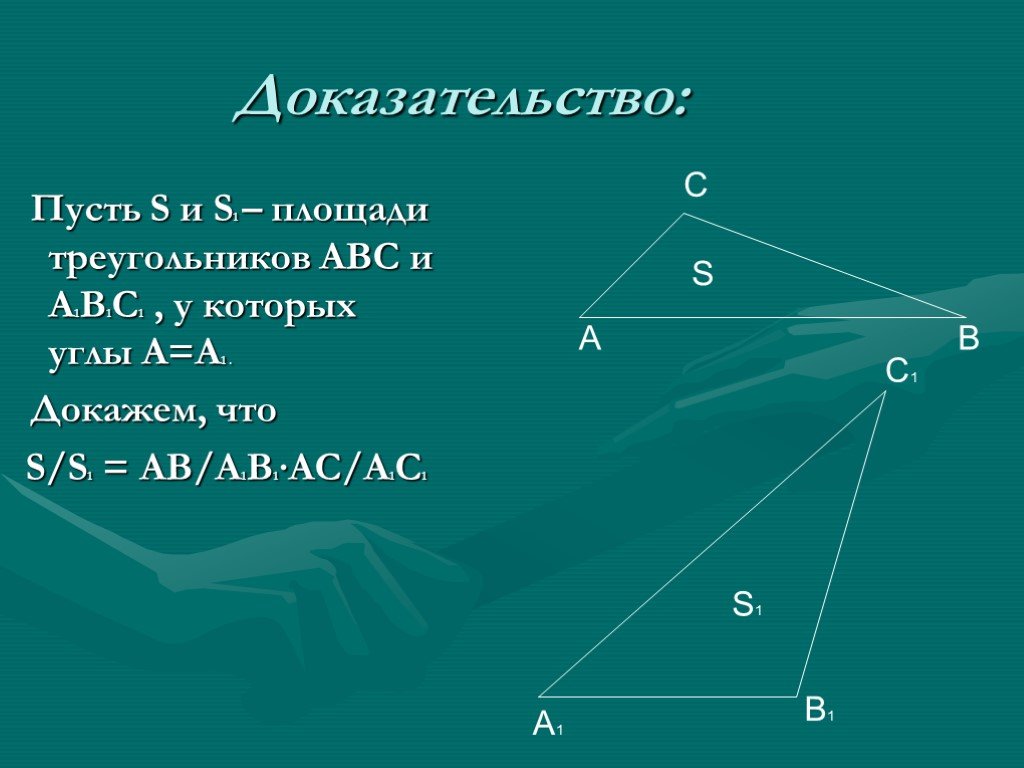
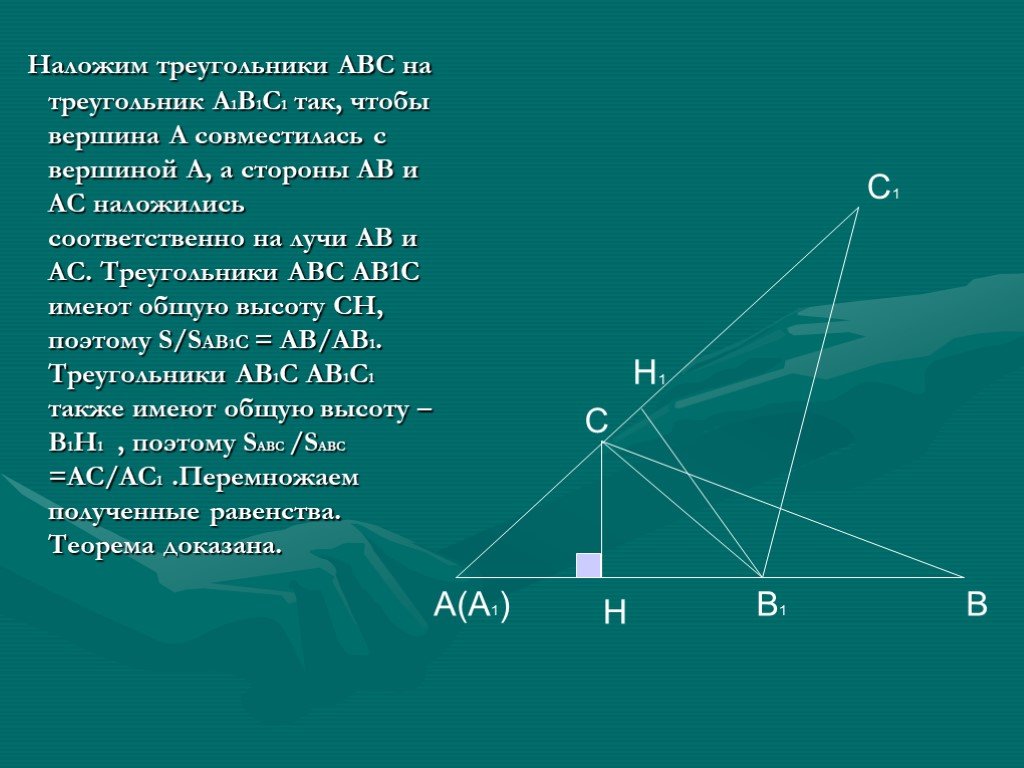
Содержание. Основные свойства площадей геометрических фигур. Площадь квадрата. Площадь прямоугольника. Площадь параллелограмма. Площадь треугольника. ...Площади фигур геометрия
Площадь- это.. Квадратный сантиметр- это площадь квадрата со стороной 1 см.. Что бы найти площадь фигуры надо определить, сколько таких квадратов ...Площади фигур. Зачёт
закрепить навык в решении задач на нахождение площадей фигур; развивать мышление, внимание. Цель:. Купи трапецию Купи параллелограмм. Купи фигуру. ...Площади фигур. Теорема Пифагора
Установите соответствие между фигурой и формулой площади. . Задача № 1. В треугольнике два угла равны 45 и 90 , а большая сторона 12 см. Найдите 2 ...Площади фигур
Основные теоретические сведения. Задачи с решениями. Задачи для самостоятельного решения. Площадь треугольника. Площадь параллелограмма. Площадь ромба ...Решение задач на готовых чертежах. Площади фигур выполнена в powerpoint
8 9 10 11 14 15 16 17 18 30 33 34 35 1 3 4 5 6 13 19 31 7. Найти: D С В А Дано:. 2. E F. B C. Е. . P M K. К М О Р. Т. . N. 450. 12. 12 см 300 8 см. ...Площади комбинированных фигур
Разминка №1. Я задумал число. Если к половине этого числа прибавить четверть его, то получится 18. какое число я задумал? Решение ? 18. №2. В доме ...Интеллектуальная игра на тему "Площади плоских фигур"
Обобщить и систематизировать знания учащихся по теме «Площади плоских фигур»: Повторить определения и свойства фигур, формулы для вычисления площади. ...Решение задач.Применение интеграла к вычислению площади и объема геометрических фигур
Найти одну из первообразных. ; ; ; . Вычислить интеграл. 1. ; 3. ; 2. ; 4. . ...Площади простых фигур
№1. а = 7 см №3. a = 7 см, = 4 см №4. = 8 см, = 5 см. Н а й д и т е п л о щ а д ь ф и г у р ы :. № 2. а= 6 см, в = 4см. б) a = 6 см, h = 5 см г) а ...Задачи на площади фигур
Квадрат и прямоугольник. Запишите формулы площади и периметра фигур: квадрата: S = Р = прямоугольника S = Р =. а b. Запишите формулы площади и периметра ...Площади плоских геометрических фигур
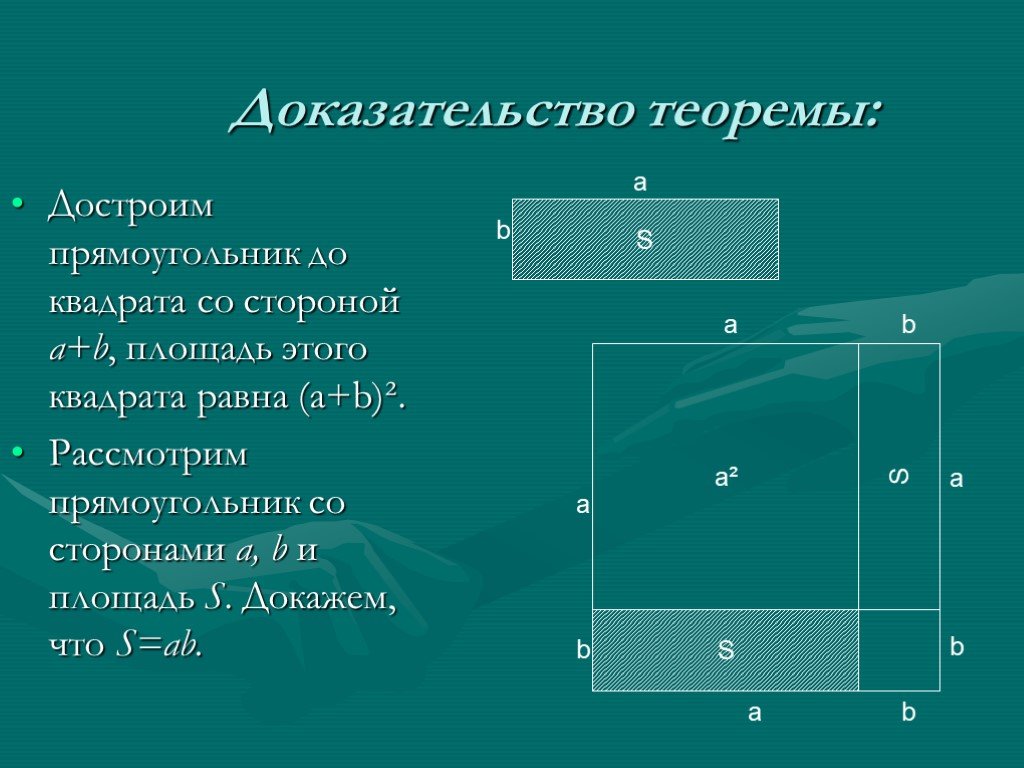
Площадь прямоугольника. a b. Площадь прямоугольника равна произведению двух его смежных сторон. Площадь квадрата равна квадрату его стороны. Площадь ...Площадь. Площади четырехугольников
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Задание: покрыть землю искусственной травой, которая представлена в виде 30 равнобедренных ...Площади четырехугольников
Параллелограмм А В С D. Параллелограмм есть четырехугольник, противоположные стороны которого попарно параллельны. Любые две противоположные стороны ...Вычисление площадей плоских фигур
Содержание. 1.Фигуры 2.Параллелограмм 3.Прямоугольник 4.Ромб 5.Квадрат 6.Треугольник 7.Трапеция 8. Круг 9.Примеры вычисления площадей фигур. Клинкова ...Вычисление площадей плоских фигур с помощью определенного интеграла
ВЫЧИСЛИТЕ ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ВЫ УЗНАЕТЕ ОДНО ИЗ ВЫСКАЗЫВАНИЙ ФРАНЦУЗСКОГО МАТЕМАТИКА С.Д.ПУАССОНА. Жизнь украшается двумя вещами: занятием математикой ...Площади многоугольников
Площади многоугольников. Площадь многоугольника. Основные свойства площадей. Площадь прямоугольника. Площадь параллелограмма. Площадь треугольника. ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Преобразование фигур на плоскости. Виды движения
Преобразование плоскости, при котором расстояние между двумя любыми точками сохраняется, называется движением. Из определения следует, что при движении ...Изображение пространственных фигур
Для изображения пространственных фигур используют параллельную проекцию. Плоскость, на которую проектируется фигура, называется плоскостью изображений, ...Конспекты
Площади фигур
Конспект урока для 8 класса по геометрии "Площади фигур". Цели урока:. повторить пройденный материал, вывести формулу нахождения площади прямоугольного ...Площади фигур
Урок по теме: « Площади фигур» - 8 класс. 19.12.2014. Учитель математики Дорофеева М.Я. МКУ « Атагайская СОШ». Нижнеудинского района. Иркутской ...Площади фигур
Обучение решению геометрических задач. ГБОУ СПО «КПК» г.Константиновска Ростовской области. Ю.В.Алексей, преподаватель информатики и математики. ...Площади фигур
Урок математики в 3Б классе по теме «Площади фигур» ( программа «Перспектива»). Планируемые результаты:. Личностные: развитие навыков сотрудничества ...Площади параллелограмма и треугольника, приложения для нахождения площадей различных фигур
Дата. . Тема:. Площади параллелограмма и треугольника, приложения для нахождения площадей различных фигур. Цель:. познакомиться с формулой Пика ...Площади плоских фигур. Пространственные тела. Площади поверхности многогранников
Приложения 1. Разработки уроков с профессиональной направленностью. Урок 1. Тема урока:. . Площади плоских фигур. Пространственные тела. Площади ...Определение площади фигур
Урок-игра по геометрии в 8 классе. . . Тема: «Определение площади фигур». Постернакова Ольга Глебовна – учитель математики. Ливадийский УВК, ...Порядок действий. Нахождение периметра и площади геометрических фигур
Урок математики. Закрепление изученного материала по теме «Порядок действий. Нахождение периметра и площади геометрических фигур» 3 класс. Вид ...Площадь. Вычисление площади фигур различной конфигурации
Геометрия. . 4 кл. Учитель: Крамаренко Н.Н. Тема:. Площадь. Вычисление площади фигур различной конфигурации. Цели:. 1) Учить находить площади ...Конструирование предметов из геометрических фигур
Фёдорова Ирина Геннадьевна, учитель начальных классов. . МС(К)ОУ для обучающихся, воспитанников с ограниченными возможностями здоровья «Специальная ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:11 июня 2019
Категория:Математика
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию