Презентация "Логические операции" по математике – проект, доклад
Презентацию на тему "Логические операции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 33 слайд(ов).
Слайды презентации
Список похожих презентаций
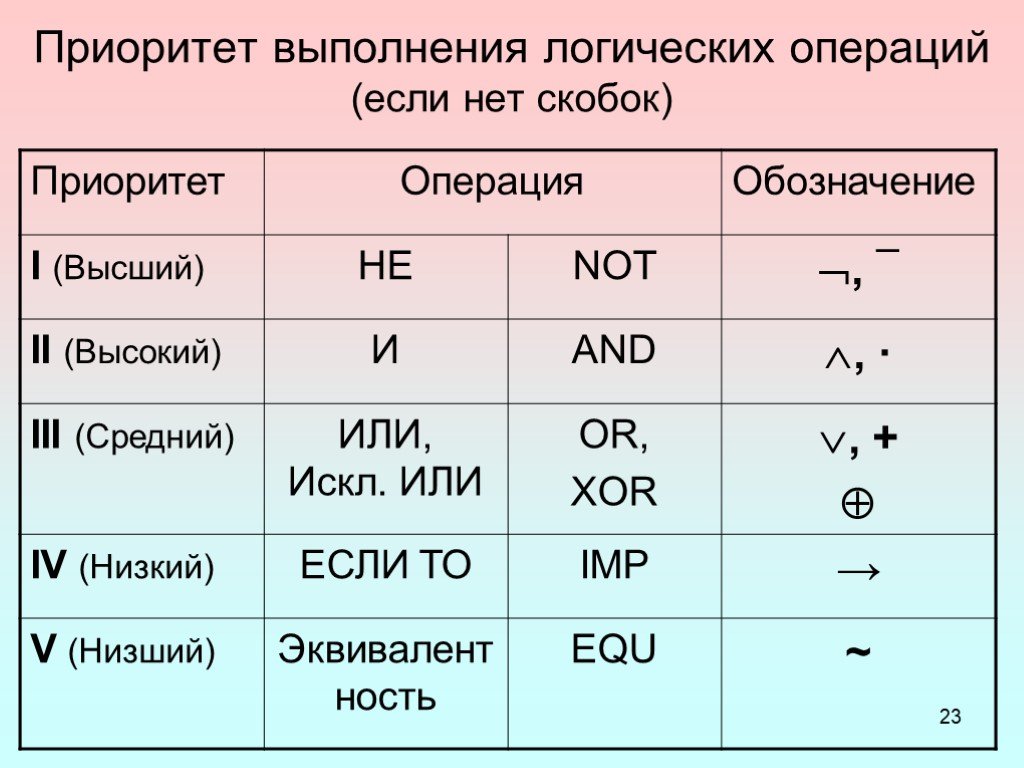
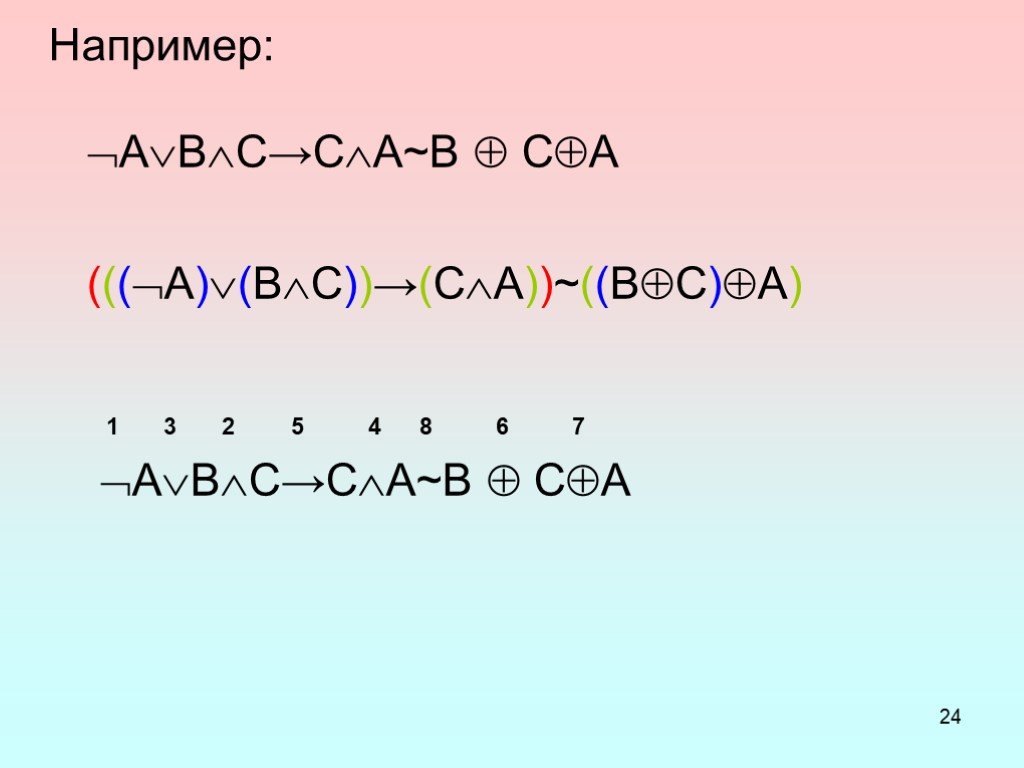
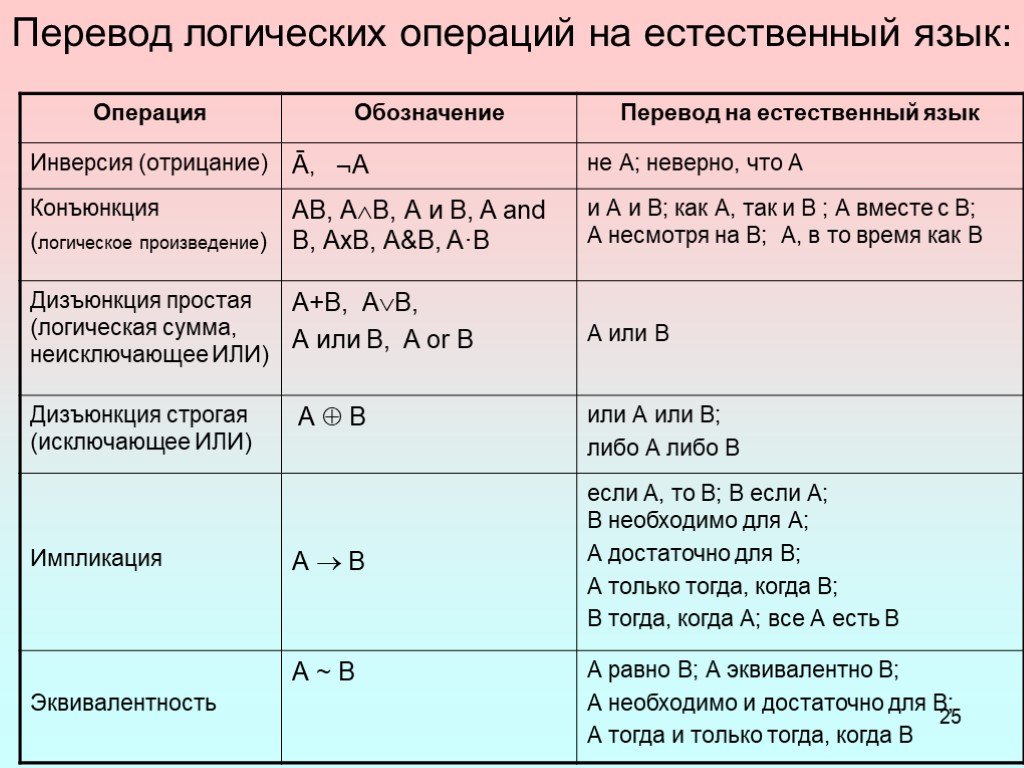
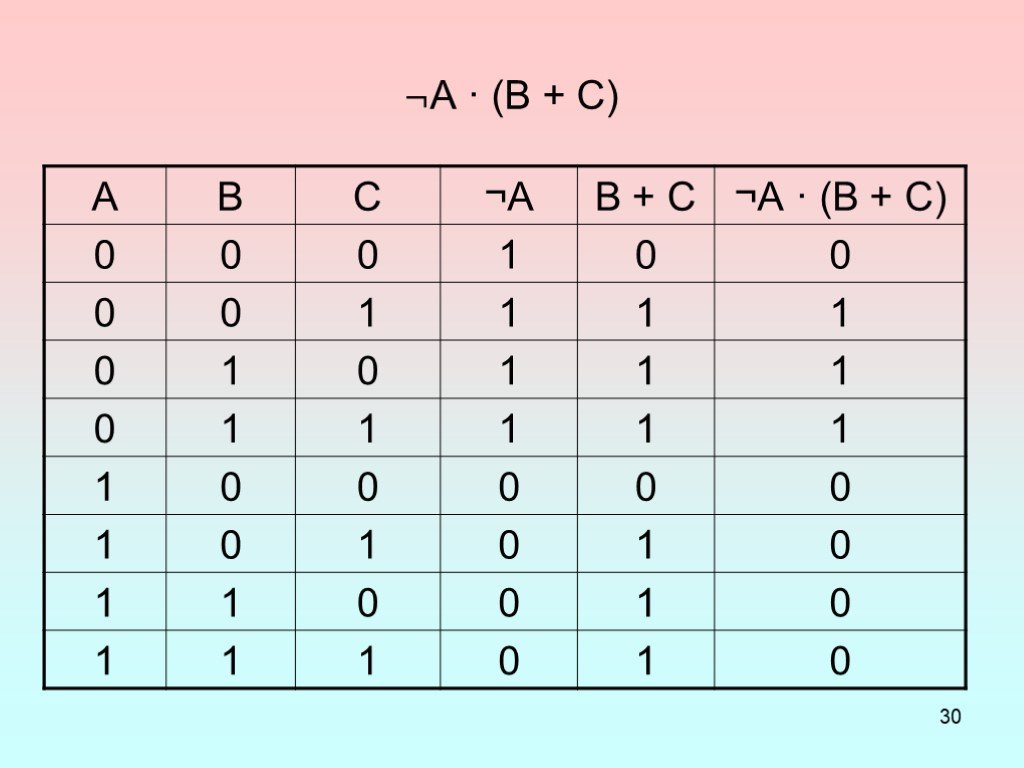
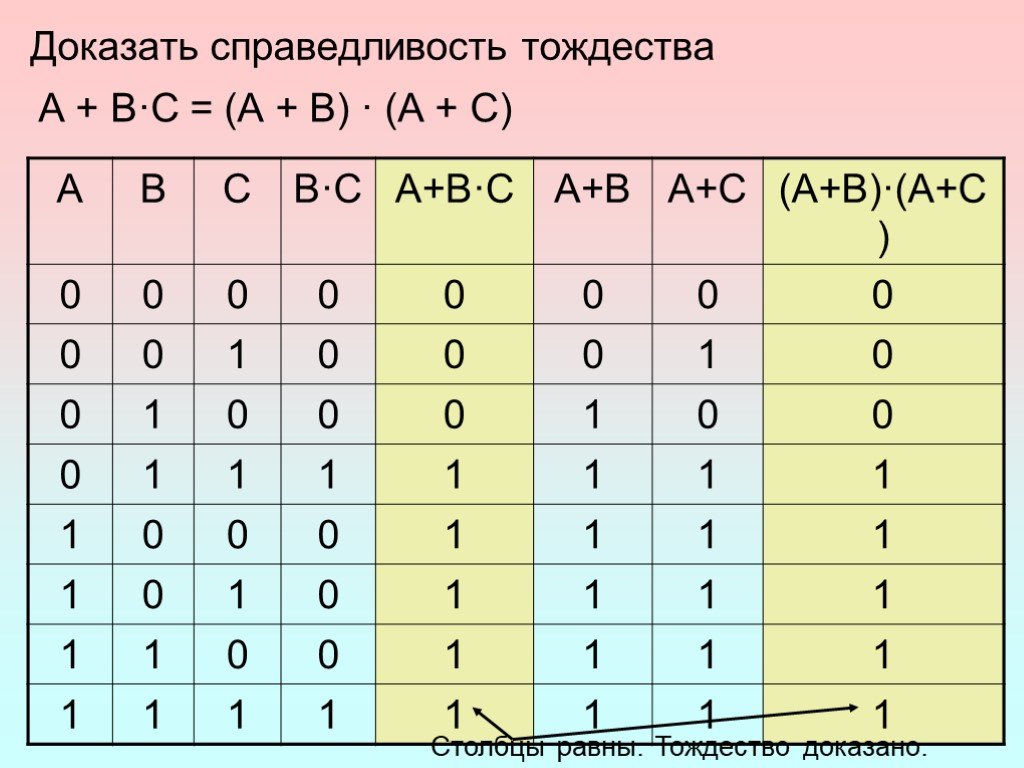
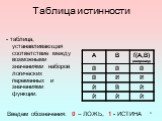
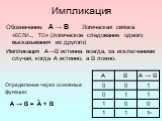
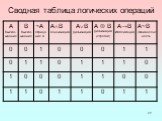
Логические операции
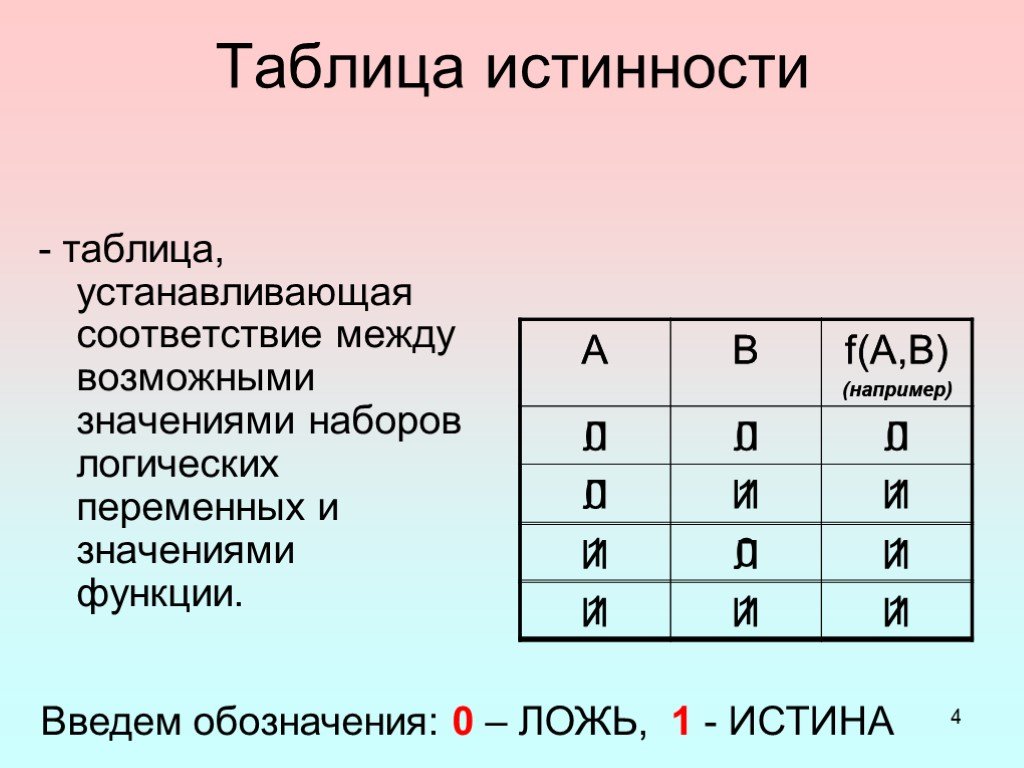
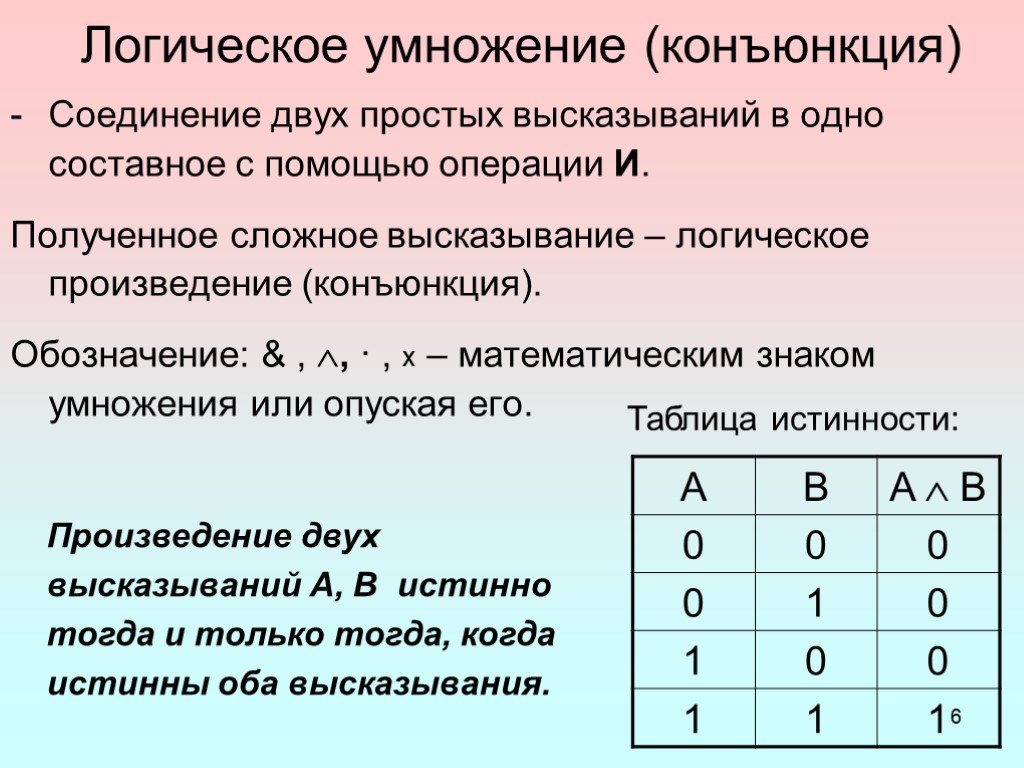
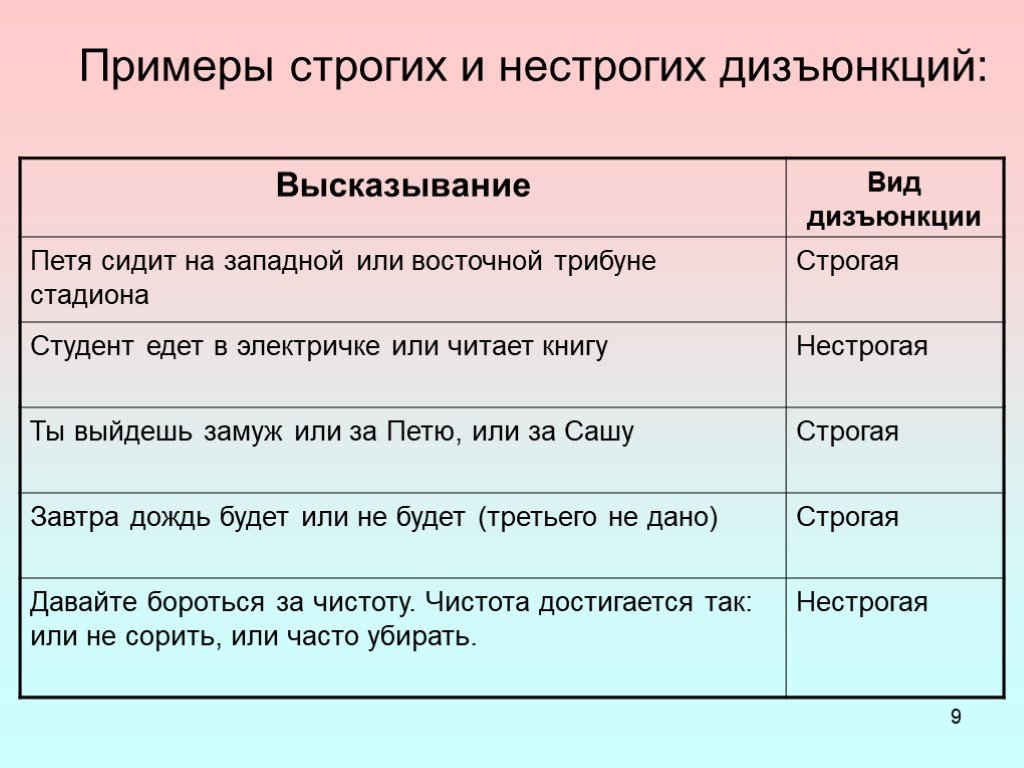
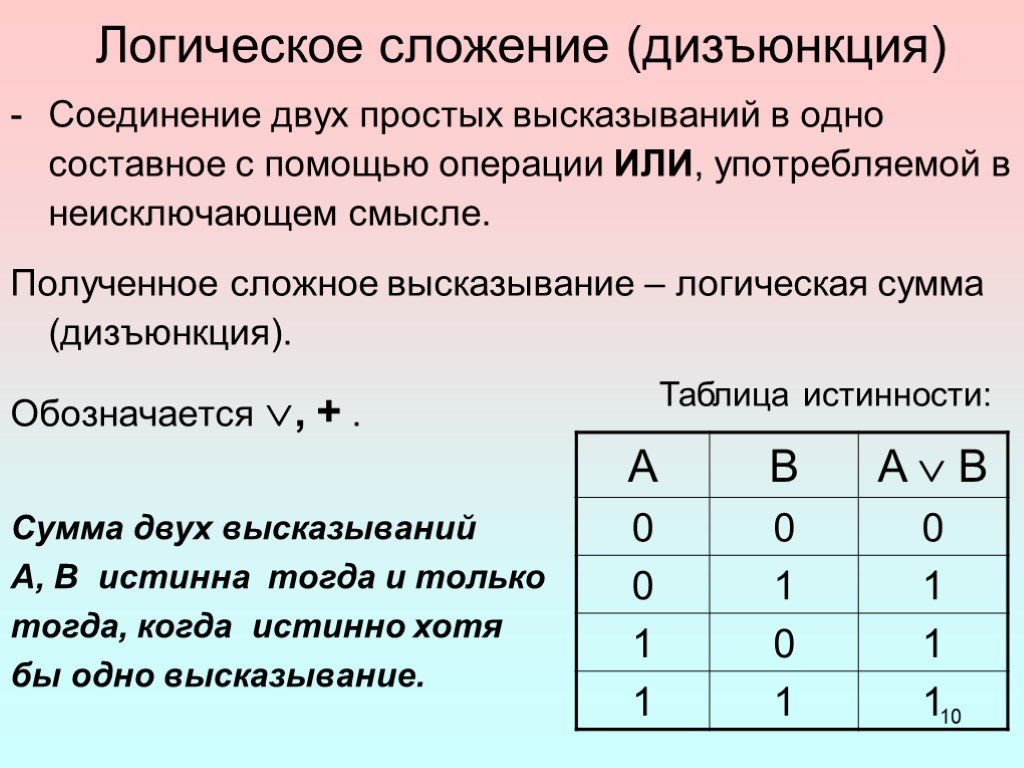
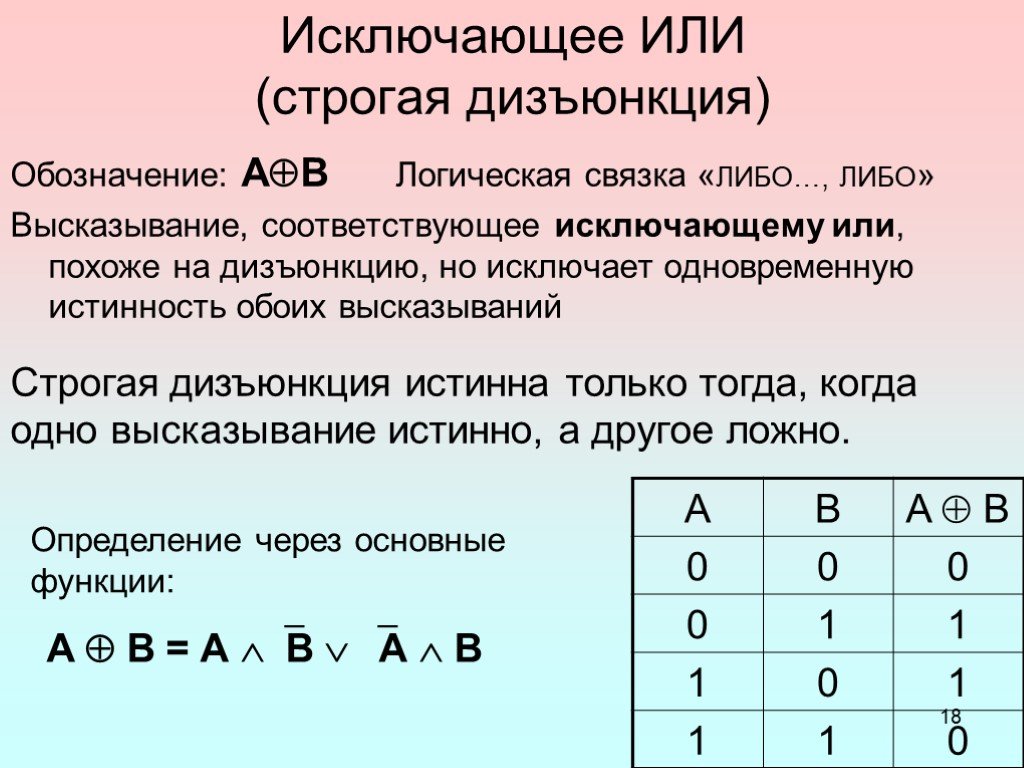
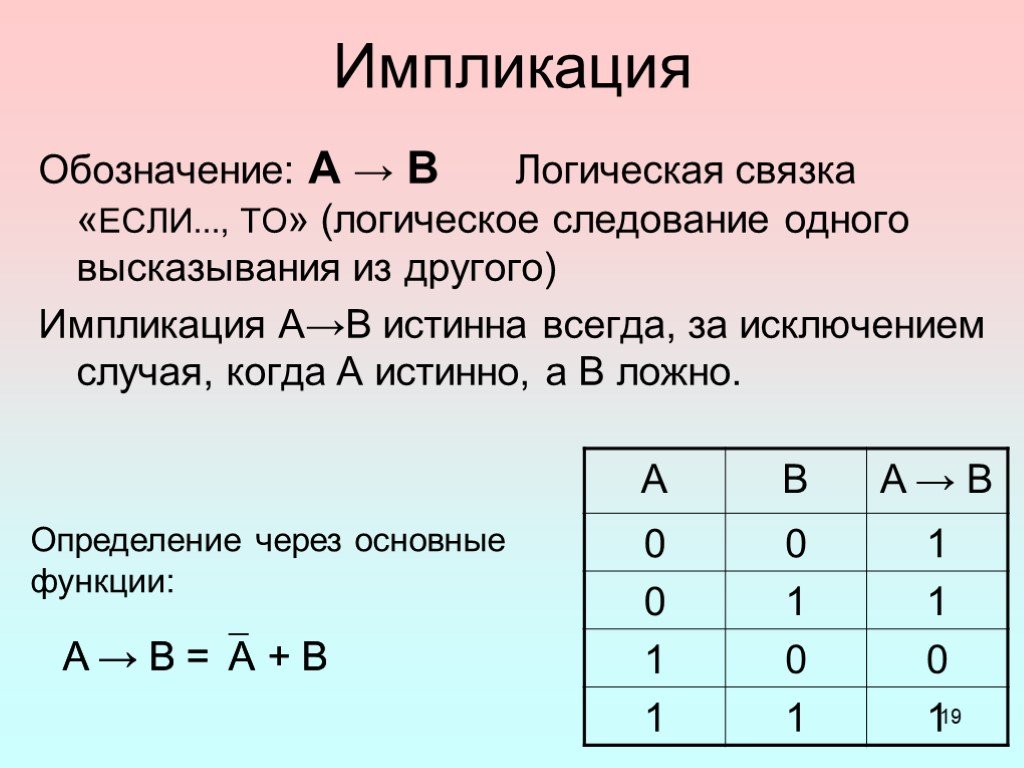
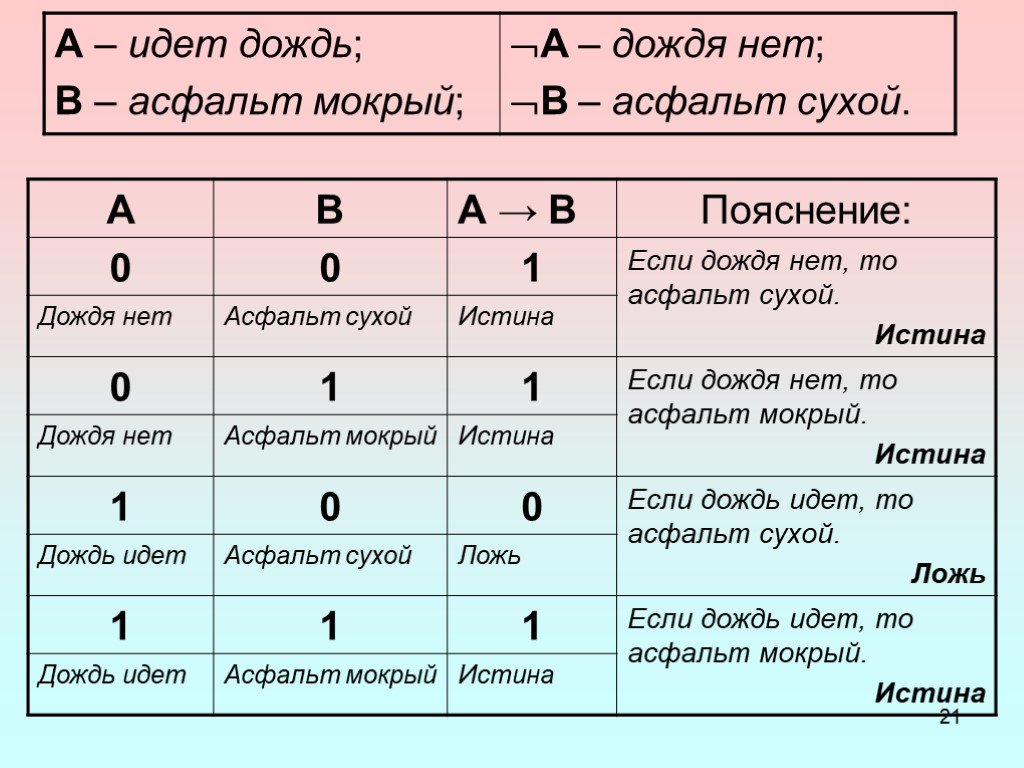
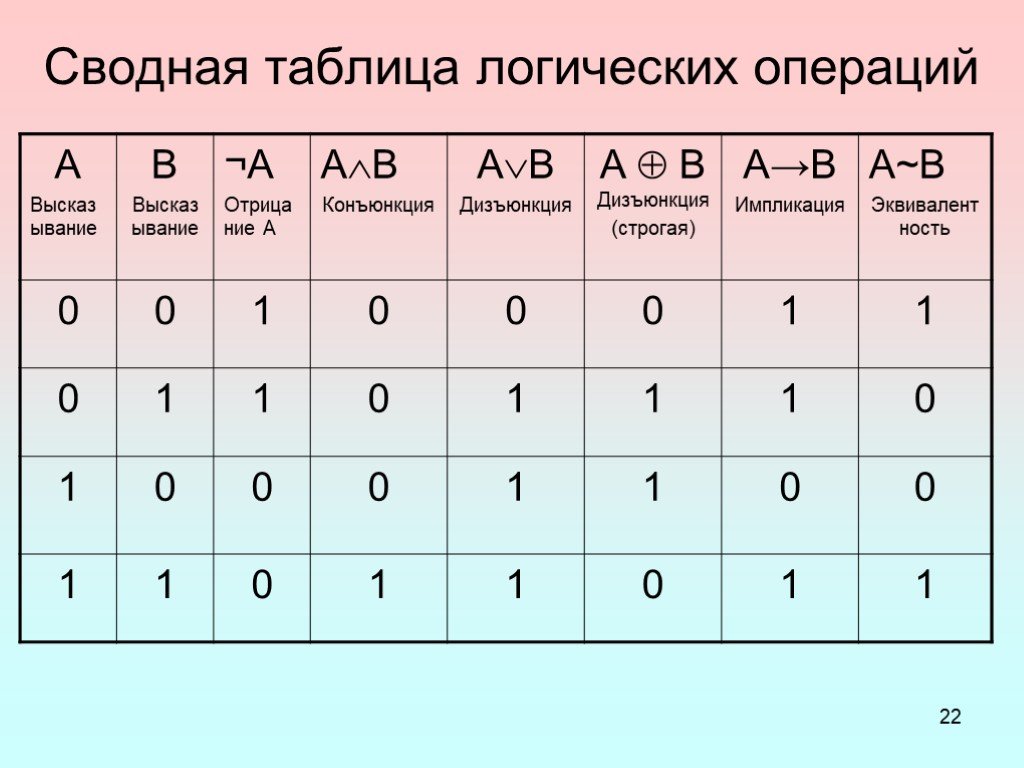
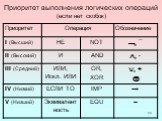
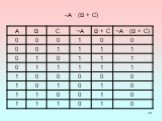
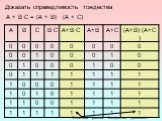
— способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями ...Одночлены. Арифметические операции над одночленами
Внимание! Выполняя тест, внимательно читайте задания. Если не можете ответить сразу, решайте номера на черновике. Если вы выбрали не правильный ответ, ...Множества и операции над ними
Множество – это совокупность однотипных элементов или объектов, объединённых по некоторому признаку, интересному для данного рассмотрения или анализа ...Множества и операции над ними
a, b, …, x, y, z – элементы множества A, B, … X, Y, Z - множества. { ; } – используется для перечисления элементов | - заменяет словосочетание «…таких, ...Логические задачи на переправу без чисел
Цель: собрать материал о логических играх без чисел, систематизировать и представить материал для работы в школьных математических кружках. Задачи. ...Логические задачки
Существует ли жизнь на Марсе и какие они — марсиане? Пофантазируем на эту тему. Может они похожи на нас, или совершено другие, какие-нибудь мюмзики ...Логические задачи для детей
В магазине было шесть разных ящиков с гвоздями. Масса ящиков в 6, 7, 8, 9, 10 ,11 кг. Два покупателя приобрели пять ящиков, причём каждому гвоздей ...Логические задачи и загадки
Введение. Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, ...Логические задачи для 1 класса
Дима выиграл у Алёши 2 партии в шахматы, а Алёша выиграл 3 партии. Сколько партий сыграли мальчики? задача 1 4 партии 5 партий 3 партии 1+1+1=3 2+1=3. ...Логические задачи
Задача «Школьные учителя». В старших классах работают три учителя: Воронов, Соколов и Коршунов. Каждый из них преподает по два предмета, так что в ...Логические задачи
Шесть школьников, участвуя в воскреснике, разбились на три брига-ды. Бригадиров звали: Володя, Петя, Вася. Володе с Мишей дали двухмет-ровые, Пете ...Логические задачи
Пётр - сын Сергея, а Сергей – сын Фёдора. Кем приходится Пётр Фёдору? задача 1 внуком сыном дедом. 2 4 6. Уменьшаемое больше вычитаемого на 2. Чему ...Операции. Обратные операции
Реши цепочку. 8 15 9 90 60 160 +7 - 6 +69 - 30 +100. Посмотрите на выражения. Что интересного вы заметили? Найдите значения выражений. 160 + 90 = ...Арифметические операции в позиционных системах счисления
Ответьте на вопросы:. Какие системы называются НЕПОЗИЦИОННЫМИ? Какие системы называются ПОЗИЦИОННЫМИ? Какое число называют – ОСНОВАНИЕ позиционной ...Синус, косинус, тангенс и котангенс, алгебра,
Синус и косинус. Что будем изучать:. Определение синуса и косинуса. Определение тангенса и котангенса. Основное тригонометрическое тождество. Примеры ...Тригонометрические функции углового аргумента - алгебра,
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Матричная алгебра в экономике
Содержание:. ● Вступление ● Что такое матрицы и операции над ними ● Решение экономических задач матричным методом ● Заключение ● Список используемой ...Реляционная алгебра – механизм манипулирования реляционными данными
Две группы операций РА. теоретико-множественные операции специальные реляционные операции. Теоретико-множественные операции. объединения отношений; ...ГИА 2013. Модуль алгебра №6
ГИА – 2013 г. Модуль «Алгебра» №6. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. ...ГИА 2013. Модуль алгебра №8
Модуль «Алгебра» №8. Повторение (4). Решите неравенство 7+2(х-4)≥х+4. Ответ: [-3;+∞). Повторение (подсказка). При решении неравенства можно переносить ...Конспекты
Обратные операции
МБОУ; Черноборская сош,Чесменский район,Челябинская область. Выполнила:. Шеметова Любовь Геннадьевна, учитель высшей категории. shemetova. _. lyubov. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:5 июня 2019
Категория:Математика
Содержит:33 слайд(ов)
Поделись с друзьями:
Скачать презентацию