Презентация "Логические операции" по математике – проект, доклад
Презентацию на тему "Логические операции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
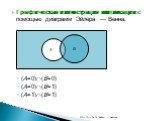
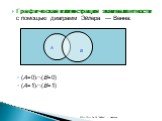
Логические операции
Высказывание в логике является аналогом выражения в арифметике: В алгебре чисел из чисел при помощи операций +, -, *, / и (,) можно составлять арифметические ...Одночлены. Арифметические операции над одночленами
Внимание! Выполняя тест, внимательно читайте задания. Если не можете ответить сразу, решайте номера на черновике. Если вы выбрали не правильный ответ, ...Множества и операции над ними
Множество – это совокупность однотипных элементов или объектов, объединённых по некоторому признаку, интересному для данного рассмотрения или анализа ...Множества и операции над ними
a, b, …, x, y, z – элементы множества A, B, … X, Y, Z - множества. { ; } – используется для перечисления элементов | - заменяет словосочетание «…таких, ...Логические задачи на переправу без чисел
Цель: собрать материал о логических играх без чисел, систематизировать и представить материал для работы в школьных математических кружках. Задачи. ...Логические задачки
Существует ли жизнь на Марсе и какие они — марсиане? Пофантазируем на эту тему. Может они похожи на нас, или совершено другие, какие-нибудь мюмзики ...Логические задачи для детей
В магазине было шесть разных ящиков с гвоздями. Масса ящиков в 6, 7, 8, 9, 10 ,11 кг. Два покупателя приобрели пять ящиков, причём каждому гвоздей ...Логические задачи и загадки
Введение. Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, ...Логические задачи для 1 класса
Дима выиграл у Алёши 2 партии в шахматы, а Алёша выиграл 3 партии. Сколько партий сыграли мальчики? задача 1 4 партии 5 партий 3 партии 1+1+1=3 2+1=3. ...Логические задачи
Задача «Школьные учителя». В старших классах работают три учителя: Воронов, Соколов и Коршунов. Каждый из них преподает по два предмета, так что в ...Логические задачи
Шесть школьников, участвуя в воскреснике, разбились на три брига-ды. Бригадиров звали: Володя, Петя, Вася. Володе с Мишей дали двухмет-ровые, Пете ...Операции. Обратные операции
Реши цепочку. 8 15 9 90 60 160 +7 - 6 +69 - 30 +100. Посмотрите на выражения. Что интересного вы заметили? Найдите значения выражений. 160 + 90 = ...Логические задачи
Пётр - сын Сергея, а Сергей – сын Фёдора. Кем приходится Пётр Фёдору? задача 1 внуком сыном дедом. 2 4 6. Уменьшаемое больше вычитаемого на 2. Чему ...Арифметические операции в позиционных системах счисления
Ответьте на вопросы:. Какие системы называются НЕПОЗИЦИОННЫМИ? Какие системы называются ПОЗИЦИОННЫМИ? Какое число называют – ОСНОВАНИЕ позиционной ...«Координатная плоскость» математика
Цели и задачи урока:. 1. Ввести понятие координатной плоскости, уметь определять координаты точек, строить точки по их координатам. 2. Развивать мышление, ...Конкурсный урок математика
У Ромы не «3», а у Лены не «3» и не «5». Кто какую отметку получил? Проверь себя! 4 5. Запомни! . . Какую из этих схем составила Таня? I способ: 90 ...Куда пропала математика?
Замочек №1. Задача 1. Часто знает и дошкольник, Что такое треугольник. А уж вам-то как не знать! Но совсем другое дело: Очень быстро и умело Треугольники ...Занимательная математика Думай, считай, отгадывай!
г.Санкт-Петербург. Ростральная колонна. телевизионная башня. Исаакиевский собор. Зимний дворец. Нева. а) Высота Ростральных колонн (в метрах). б) ...Интересная математика
Франция Герб Франции Флаг Франции. . Страна граничит с 8 странами: Италией, Испанией, Бельгией, Люксембургом, Германией, Швейцарией, Монако и Андоррой. ...Занимательная математика
Добрый день! Приветствую вас, мои юные друзья математики. Удачи вам! Ваш друг Математик. Славянская кириллическая десятеричная алфавитная нумерация. ...Конспекты
Обратные операции
МБОУ; Черноборская сош,Чесменский район,Челябинская область. Выполнила:. Шеметова Любовь Геннадьевна, учитель высшей категории. shemetova. _. lyubov. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:18 сентября 2019
Категория:Математика
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию