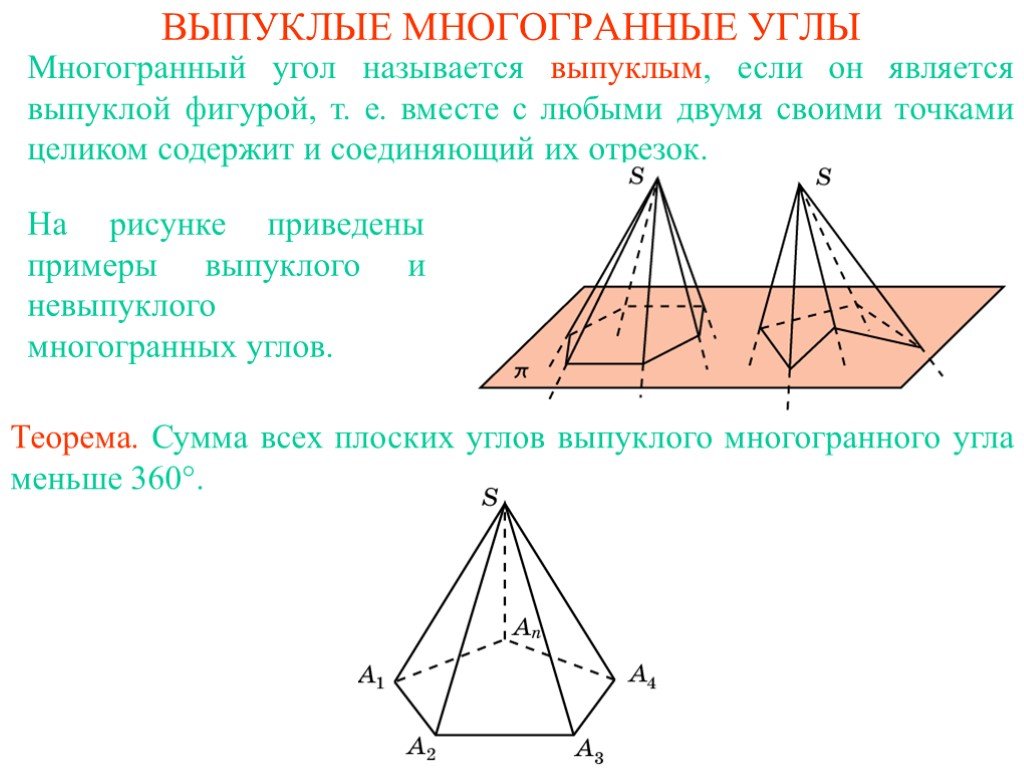
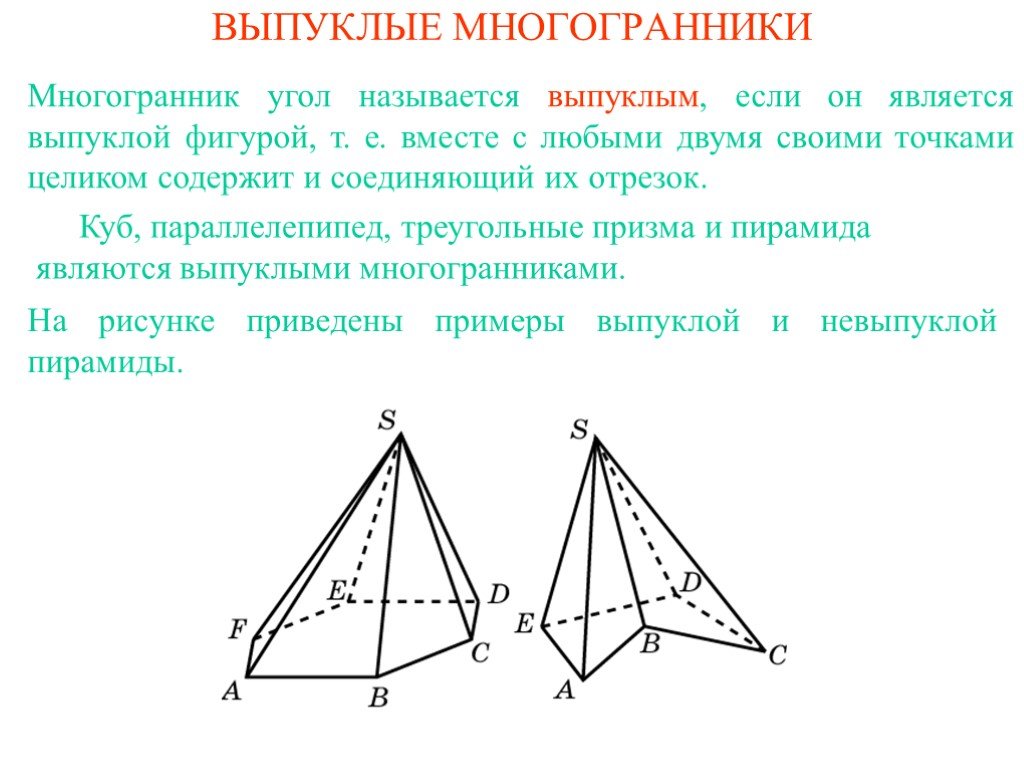
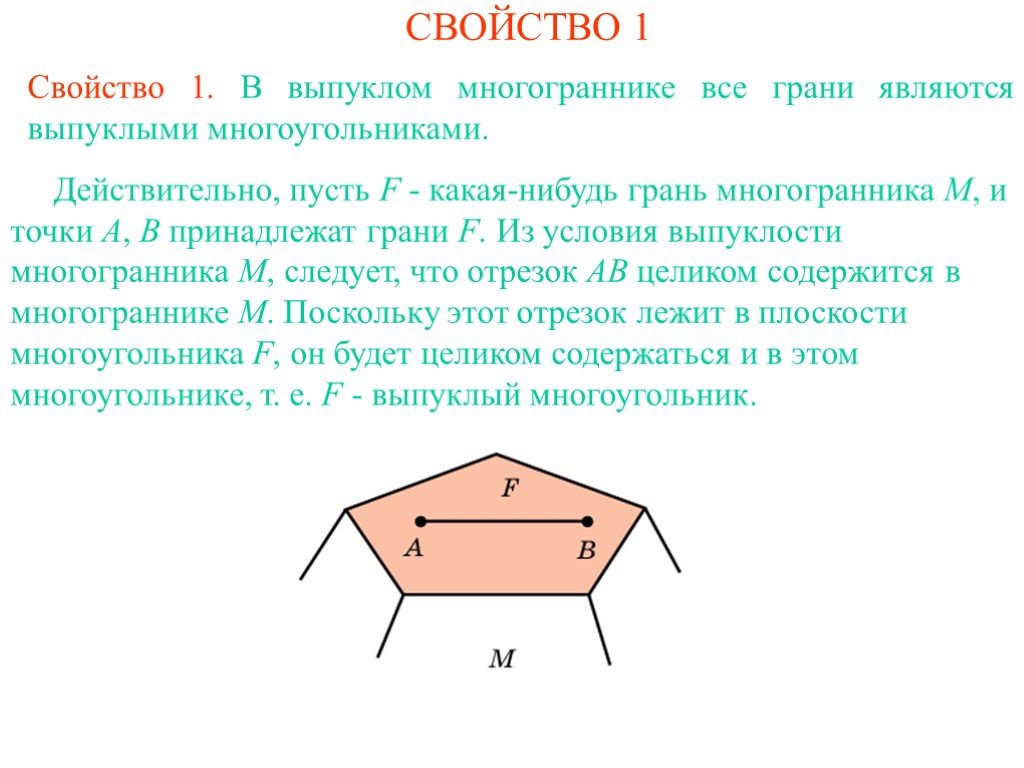
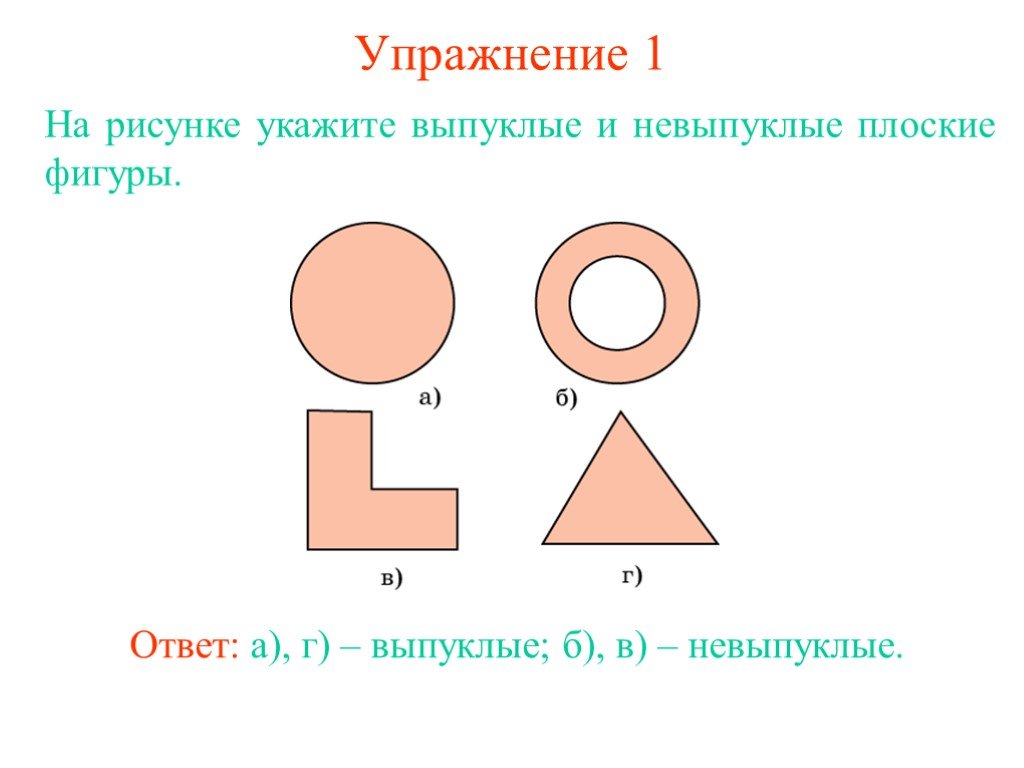
Презентация "Выпуклые многогранные углы" по математике – проект, доклад
Презентацию на тему "Выпуклые многогранные углы" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
Слайды презентации
Список похожих презентаций
Многогранные углы
В зависимости от числа граней многогранные углы бывают трехгранными, четырехгранными, пятигранными и т. д. ТРЕХГРАННЫЕ УГЛЫ.Теорема. Всякий плоский ...
Смежные и вертикальные углы геометрия
Цели урока:. Познакомить учащихся с понятиями смежных и вертикальных углов. Научить строить угол, смежный с данным. Научить строить вертикальные углы. ...Смежные и вертикальные углы
Цель: ввести понятие смежных и вертикальных углов, рассмотреть их свойства. Повторение: дерево знаний. 1. Что такое луч? Как он обозначается? 2. Какая ...Вертикальные углы
Какие полупрямые называются дополнительными? Дайте определение угла. Какие углы называются смежными? Каким свойством обладают смежные углы? Один из ...Центральные и вписанные углы
Содержание: 1. Определение и величина центрального угла. 2. Определение и величина вписанного угла. 3. Свойства вписанных углов. Угол с вершиной в ...Устные упражнения на уроках геометрии. Смежные и вертикальные углы
. . . . . . . . . . . . . . . . №17. ...Стороны и углы прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника. Мама мой взяла листок, И загнула уголок, Угол вот такой у взрослых Называется ПРЯМЫМ. ...Смежные углы
Познакомиться с определением смежных углов, с теоремой о смежных углах и ее доказательством, со следствиями из теоремы о смежных углах, с видами углов. ...Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы
8 9 10 11 14 15 16 17 18 30 1 3 4 5 6 13 19 7 31. Найти: Дано: B О А 2 1,5. С К ? . . 12 600. . . . Доп. М N. C D E. M K. A P. . . 300 O. 400 500. ...Решение задач на вписанные углы
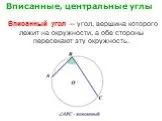
Углы, вписанные в окружность. Угол, вершина которого принадлежит окружности, а стороны пересекают окружность, называют вписанным. ∠АВС – вписанный ...Проценты и углы
Запишите ? ? ? % в виде десятичной дроби. 0,1375 1,375 137,5 0,01375. Запишите дробь ?? ??? в виде процентов. 120% 0,12% 1,2% 12%. Сколько процентов ...Вписанные, центральные углы
Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается. Задача 1. Найдите вписанный ...Вписанные углы
Устная работа. Дано: АВ : ВС : АС=2:3:4 Найти: АОВ, ВОС, АОС. Дано: МОN=EOK, MON : NOK : MOE= 3:4:5 Найти: МЕ, NK, КЕ. Угол вершина ...Вписанные и центральные углы
Вспоминаем пройденное:. Теорема о вписанном угле Вписанный угол измеряется половиной дуги, на которую опирается. Следствие 1. Вписанные углы, опирающиеся ...Смежные углы
Определение. В определении смежных углов содержатся три условия: угла – два; есть общая сторона; две другие стороны – дополнительные лучи. Проведем ...Смежные углы
Оглавлление. Определение смежных углов. Сумма смежных углов. Следствия из теоремы. Виды углов (прямой, острый, тупой). Задача. Два угла называются ...Смежные углы
Оглавлление. Определение смежных углов. Сумма смежных углов. Следствия из теоремы. Виды углов (прямой, острый, тупой). Задача. Два угла называются ...Смежные и вертикальные углы
Математический диктант. 1) Закончите предложение: «Если углы смежные, то их сумма...» 2) Сколько можно построить углов смежных с с данным? 3) Сколько ...Смежные углы и вертикальные углы
Сколько углов изображено на рисунке? Какие это углы? Существует ли взаимосвязь между этими углами? А С В О. Для всякой ли пары смежных углов выполняется ...Смежные и вертикальные углы
"Геометрия - это наука хорошо измерять. П.Рамус". . ответ:. . . . . . ...Конспекты
Смежные углы
Конструкт урока. Предмет:. математика. Класс:. 7. Тип урока:. Открытие новых знаний. Тема:. Смежные углы. Цель:. Сформировать представление ...Смежные углы
Тема урока «Смежные углы». Тип урока: урок «открытия» нового знания. Цели урока:. . Систематизировать представление о смежных углах. . ...Смежные и вертикальные углы
Конспект урока математики для 7 класса «. Смежные и вертикальные углы». Смирнова Галина Александровна. учитель математики. МКОУ Брединская СОШ ...Смежные углы
Тема:. . Смежные углы. Учитель. : Хорошун И.Г. учитель математики МОУ СОШ с. Песчаноозерка. Класс:. 7. Цели:. ввести понятие смежных углов, ...Смежные и вертикальные углы
Автор: Жданова Мария Власовна, учитель математики,. МАОУ «Кондратовская СОШ». План – конспект открытого урока математики в 5а классе в рамках ...Смежные и вертикальные углы
государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа с. Пестравка. . Открытый урок ...Прямой , тупой и острый углы
Урок математики во 2 классе. «-----------» ---------- 201 ----уч. год. Тема урока: Прямой , тупой и острый углы. Цели урока. :. . .Научить детей ...Как сравнить углы. Как измерить углы
Конспект урока математики с применением ИКТ по теме «Как сравнить углы. Как измерить углы», проведённого в 3 классе. Цель:. Создать условия для ...Как обозначают и сравнивают углы
План-конспект. Урока математики в 5 классе. . по теме «Как обозначают и сравнивают углы». по учебнику под редакцией Дорофева И.Ф. и Шарыгина ...Вписанные и центральные углы
8 класс «Вписанные и центральные углы». Цели урока. Образовательные: подготовить учащихся к успешной сдачи ГИА. Воспитательные:. . активизация ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 июня 2019
Категория:Математика
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию