Презентация "Смежные углы" по математике – проект, доклад
Презентацию на тему "Смежные углы" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
Слайды презентации
Список похожих презентаций
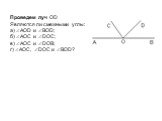
Смежные углы
Познакомиться с определением смежных углов, с теоремой о смежных углах и ее доказательством, со следствиями из теоремы о смежных углах, с видами углов. ...Смежные углы
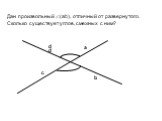
Оглавлление. Определение смежных углов. Сумма смежных углов. Следствия из теоремы. Виды углов (прямой, острый, тупой). Задача. Два угла называются ...Смежные углы и вертикальные углы
Сколько углов изображено на рисунке? Какие это углы? Существует ли взаимосвязь между этими углами? А С В О. Для всякой ли пары смежных углов выполняется ...Смежные и вертикальные углы
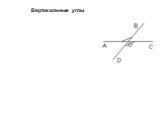
Цели урока. ознакомить учащихся с понятиями смежных и вертикальных углов, рассмотреть их свойства; научить строить угол, смежный с данным углом, изображать ...Вертикальные и смежные углы
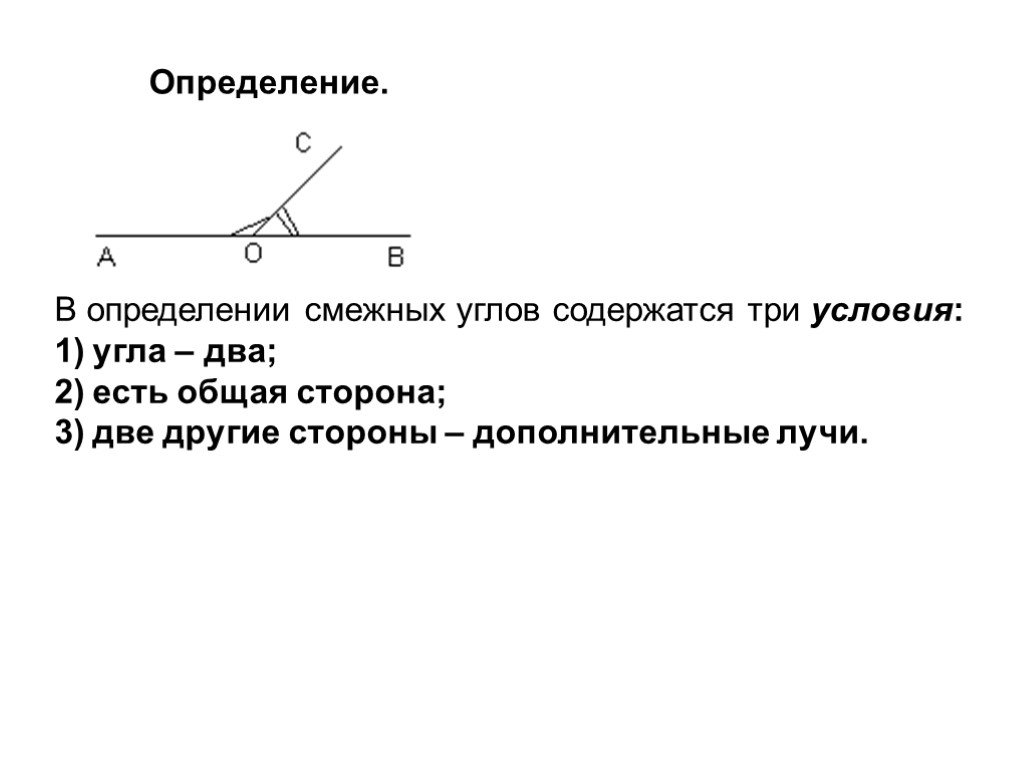
Теоретический материал. Определение . Два угла называются смежными , если у них одна сторона общая , а другие стороны этих углов являются дополнительными ...Смежные и вертикальные углы
Цель: ввести понятие смежных и вертикальных углов, рассмотреть их свойства. Повторение: дерево знаний. 1. Что такое луч? Как он обозначается? 2. Какая ...Смежные и вертикальные углы геометрия
Цели урока:. Познакомить учащихся с понятиями смежных и вертикальных углов. Научить строить угол, смежный с данным. Научить строить вертикальные углы. ...тренажёр по теме смежные и вертикальные углы
Единицей измерения углов в геометрии является- градус да, конечно Нет. Бывают углы для измерения которых используют другие единицы измерения. Вы не ...Смежные и вертикальные углы
2009 год Проект:. Выполнила: ученица 7 класса МОУ Петровской СОШ Балута Анастасия. Руководитель: учитель математики высшей категории Орлюк Вера Александровна. ...Смежные и вертикальные углы. Решение задач
Повторение. Определение: два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. А В С Д и - ...Смежные и вертикальные углы
"Геометрия - это наука хорошо измерять. П.Рамус". . ответ:. . . . . . ...Смежные и вертикальные углы
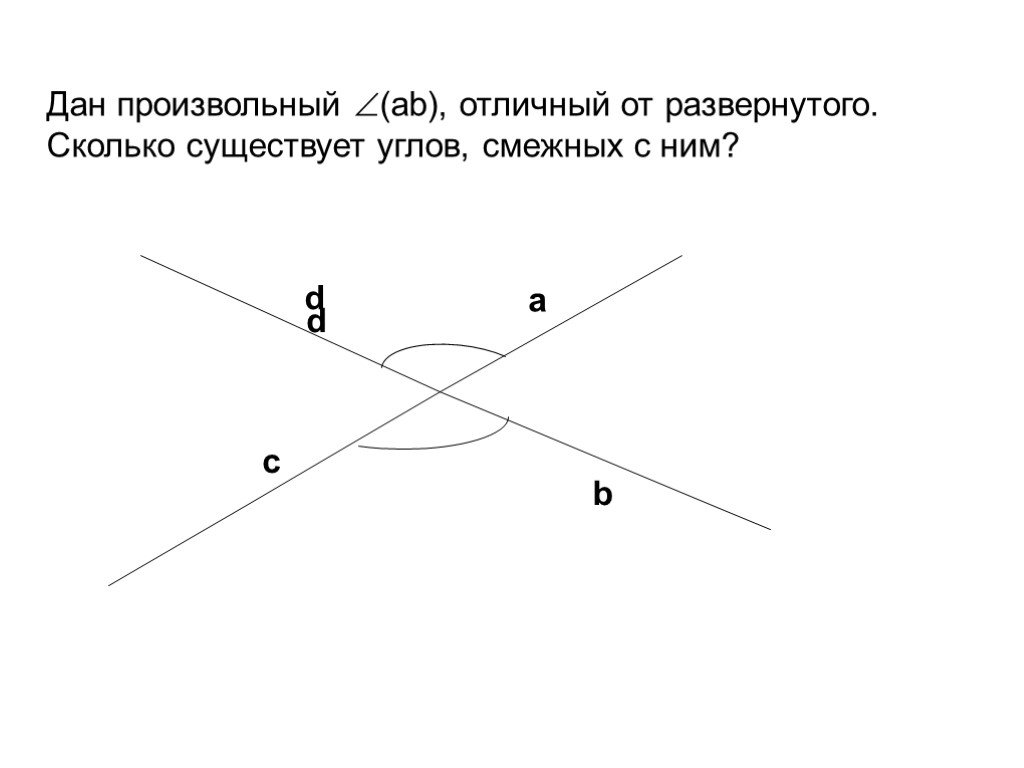
Математический диктант. 1) Закончите предложение: «Если углы смежные, то их сумма...» 2) Сколько можно построить углов смежных с с данным? 3) Сколько ...Смежные углы
Оглавлление. Определение смежных углов. Сумма смежных углов. Следствия из теоремы. Виды углов (прямой, острый, тупой). Задача. Два угла называются ...Устные упражнения на уроках геометрии. Смежные и вертикальные углы
. . . . . . . . . . . . . . . . №17. ...Стороны и углы прямоугольного треугольника
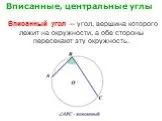
Соотношения между сторонами и углами прямоугольного треугольника. Мама мой взяла листок, И загнула уголок, Угол вот такой у взрослых Называется ПРЯМЫМ. ...Вписанные и центральные углы
Вспоминаем пройденное:. Теорема о вписанном угле Вписанный угол измеряется половиной дуги, на которую опирается. Следствие 1. Вписанные углы, опирающиеся ...Вписанные углы
Устная работа. Дано: АВ : ВС : АС=2:3:4 Найти: АОВ, ВОС, АОС. Дано: МОN=EOK, MON : NOK : MOE= 3:4:5 Найти: МЕ, NK, КЕ. Угол вершина ...Вписанные, центральные углы
Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается. Задача 1. Найдите вписанный ...Решение задач на вписанные углы
Углы, вписанные в окружность. Угол, вершина которого принадлежит окружности, а стороны пересекают окружность, называют вписанным. ∠АВС – вписанный ...Центральные и вписанные углы
Содержание: 1. Определение и величина центрального угла. 2. Определение и величина вписанного угла. 3. Свойства вписанных углов. Угол с вершиной в ...Конспекты
Смежные углы
Конструкт урока. Предмет:. математика. Класс:. 7. Тип урока:. Открытие новых знаний. Тема:. Смежные углы. Цель:. Сформировать представление ...Смежные углы
Тема урока «Смежные углы». Тип урока: урок «открытия» нового знания. Цели урока:. . Систематизировать представление о смежных углах. . ...Смежные углы
Тема:. . Смежные углы. Учитель. : Хорошун И.Г. учитель математики МОУ СОШ с. Песчаноозерка. Класс:. 7. Цели:. ввести понятие смежных углов, ...Смежные и вертикальные углы
Конспект урока математики для 7 класса «. Смежные и вертикальные углы». Смирнова Галина Александровна. учитель математики. МКОУ Брединская СОШ ...Смежные и вертикальные углы
Автор: Жданова Мария Власовна, учитель математики,. МАОУ «Кондратовская СОШ». План – конспект открытого урока математики в 5а классе в рамках ...Смежные и вертикальные углы
государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа с. Пестравка. . Открытый урок ...Вертикальные и смежные углы
Предмет. : Геометрия. Класс. 7-8. Тема урока. 7 класса: Вертикальные и смежные углы. Тип урока. : изучение нового материала. Цель урока:. ...Прямой , тупой и острый углы
Урок математики во 2 классе. «-----------» ---------- 201 ----уч. год. Тема урока: Прямой , тупой и острый углы. Цели урока. :. . .Научить детей ...Как сравнить углы. Как измерить углы
Конспект урока математики с применением ИКТ по теме «Как сравнить углы. Как измерить углы», проведённого в 3 классе. Цель:. Создать условия для ...Как обозначают и сравнивают углы
План-конспект. Урока математики в 5 классе. . по теме «Как обозначают и сравнивают углы». по учебнику под редакцией Дорофева И.Ф. и Шарыгина ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 августа 2019
Категория:Математика
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию