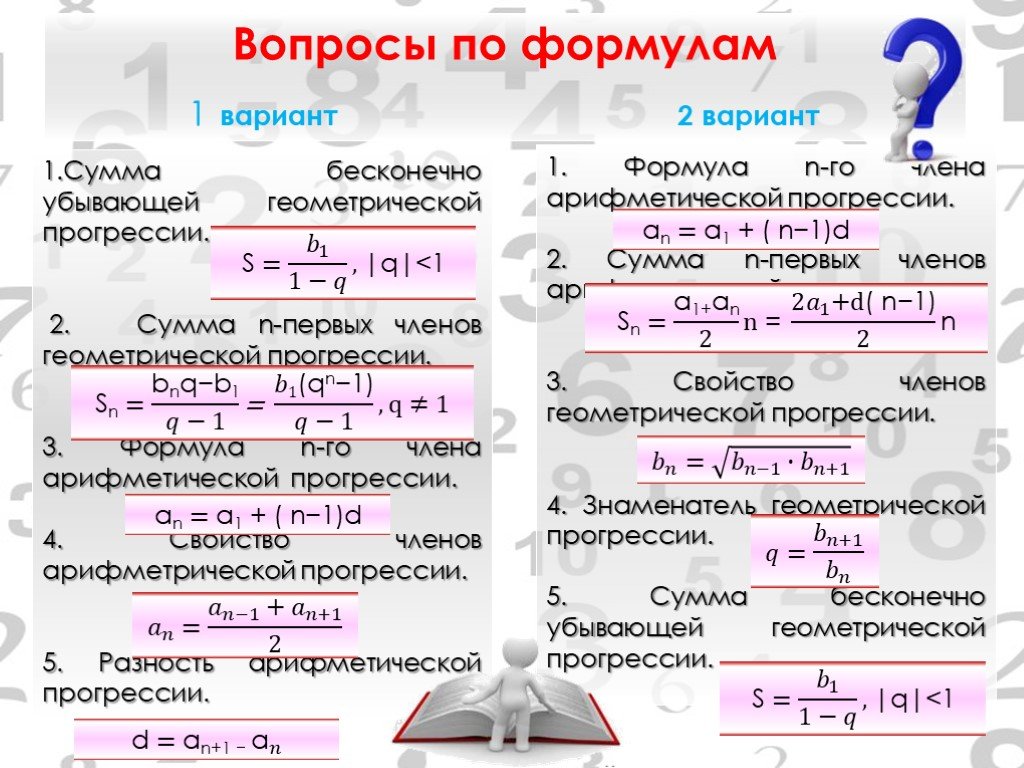
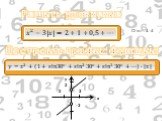
Презентация "Арифметическая и геометрическая прогрессии" по математике – проект, доклад
Презентацию на тему "Арифметическая и геометрическая прогрессии" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
"Арифметическая прогрессия" Викторина
Первый раунд. Устная работа Каждый правильный ответ приносит один балл. Что означает слово «Прогрессия»? В последовательности (Хn) назовите первый, ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии. 1)Какова бы ни была плоскость, существуют точки, принадлежащие ей и точки, не принадлежащие ей. 2) Если две плоскости имеют ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ...Cфера и шар
Что такое сфера и шар? геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние ...«Умножение и деление»
Цели урока. Обобщение и систематизация знаний, умений и навыков по теме: «Умножение и деление натуральных чисел»; контроль уровня усвоения темы. Развитие ...«Табличное умножение и деление» Устный счёт
Решите задачу: Во раз б 9 шт. 3 шт.. 9:3=3 (раза)- во столько раз апельсинов больше, чем яблок. 7∙5=35 (яб.). У резной избушки На лесной опушке Бельчата ...«Сложение и вычитание десятичных дробей»
Чтобы сложить (вычесть) десятичные дроби, нужно: 1) уравнять в этих дробях количество знаков после запятой; 2) записать их друг под другом так, чтобы ..."Функция y = kx², ее свойства и график". 8-й класс
Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ..."Умножение и деление чисел"
Тема урока:. Умножение и Деление чисел. В наше время, чтобы строить И машиной управлять, Помни друг, что надо прочно Математику познать! Математический ..."Турнир веселых и смекалистых знатоков истории, физики, химии, математики"
Цели мероприятия: 1.Развитие у учащихся интереса к изучаемым предметам. 2.Показать необходимость знаний по математике в других науках. 3.Формирование ..."Сложение положительных и отрицательных чисел"
Старостенко Алла Николаевна, учитель математики Предмет: математика, урок-игра, закрепление изученного материала Тема: «Сложение положительных и отрицательных ..."Сложение и вычитание рациональных чисел"
I. II. III. IV. Тема: "Сложение и вычитание положительных и отрицательных чисел". Станции: Историческая Биологическая Географическая Математическая. ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ..."Комбинаторика и вероятность"
Диктант ******- это раздел математики, посвященный задачам выбора и расположения предметов из различных множеств. Произведение натуральных чисел от ...Активные методы обучения на уроках математики и во внеурочной деятельности
Активные методы обучения — это методы, которые побуждают учащихся к активной мыслительной и практической деятельности в процессе овладения учебным ..."Доли и дроби"
Семья Долиных:. Бабушка Доля Дедушка Доль Внуки Дробик и Долюша. Бабушка доля очень любит печь пироги. Дробик пришел с фермы очень голодный. разрезал ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ...«Сложение положительных и отрицательных чисел».
. Кемеровская область. Если в картину Сибири всмотреться, На ней обозначены контуры сердца. И бьется оно. И отчизна внимает Рабочему ритму Кузнецкого ..."Число и цифра 9"
Число и цифра 9. Тема урока:. Цель урока:. познакомить с числом 9, обучить написанию цифры 9. Задачи урока:. вспомнить времена года, дни недели, месяцы; ...Конспекты
Арифметическая и геометрическая прогрессии
Министерство образования и науки Республики Казахстан. Атбасарский районный отдел образования. Акмолинской области. Открытый урок по алгебре ...Арифметическая и геометрическая прогрессии
Учитель:Корабельникова Г.А. . . Дата проведения: 30.01.09. . . . Урок алгебры в 9-м классе. . Тема :« Арифметическая и геометрическая прогрессии». ...Арифметическая и геометрическая прогрессии
Муниципальное бюджетное общеобразовательное учреждение. « Октябрьская школа-гимназия». Красногвардейского района Республика Крым. ...Арифметическая и геометрическая прогрессии
Тема: Арифметическая и геометрическая прогрессии. Тип урока:. урок обобщения и систематизации знаний. Цель:. актуализация имеющиеся знания ...Арифметическая и геометрическая прогрессии
Тема урока:. «Арифметическая и геометрическая прогрессии». . Цель урока:. Систематизировать и обобщить знания учащихся по теме «Арифметическая и ...Арифметическая и геометрическая прогрессии
Тип урока:. урок обобщения и систематизации знаний. Цель урока:. обобщить, систематизировать и расширить знания, умения и навыки учащихся при ...Арифметическая и геометрическая прогрессии
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ. . СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №1918. . Конспект урока по алгебре ...Арифметическая и геометрическая прогрессии
Ф.И.О автора материала. :. Дыда Татьяна Ивановна. Место работы. :. МАОУ СОШ № 18, г. Армавир, Краснодарский край. Должность. :. Учитель математики. ...Арифметическая и геометрическая прогрессии
Разработка урока алгебры 9 класс. по теме :. «Арифметическая и геометрическая прогрессии». Тема урока. : Прогрессио- движение вперед. Цель урока. ...Арифметическая и геометрическая прогрессии
Технологическая карта урока. Учебный предмет: алгебра. Класс: 9. Школа: МБОУ «Большебитаманская» СОШ. Учитель: Мухаметзянова Эльмира Габдулловна. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 мая 2019
Категория:Математика
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию