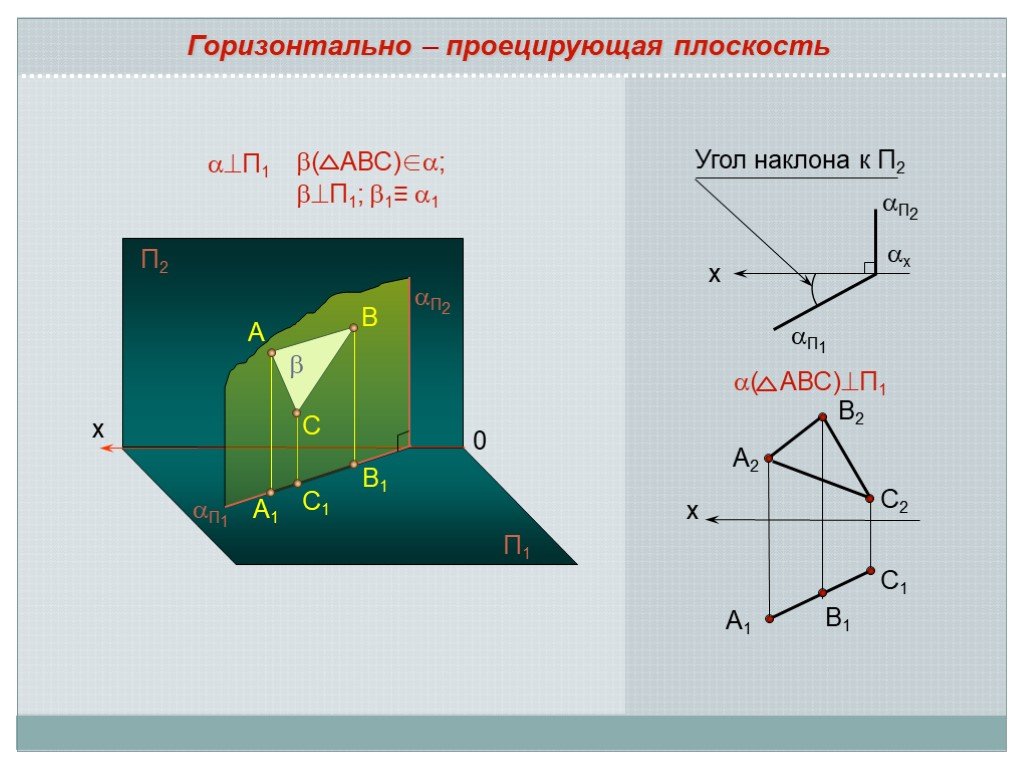
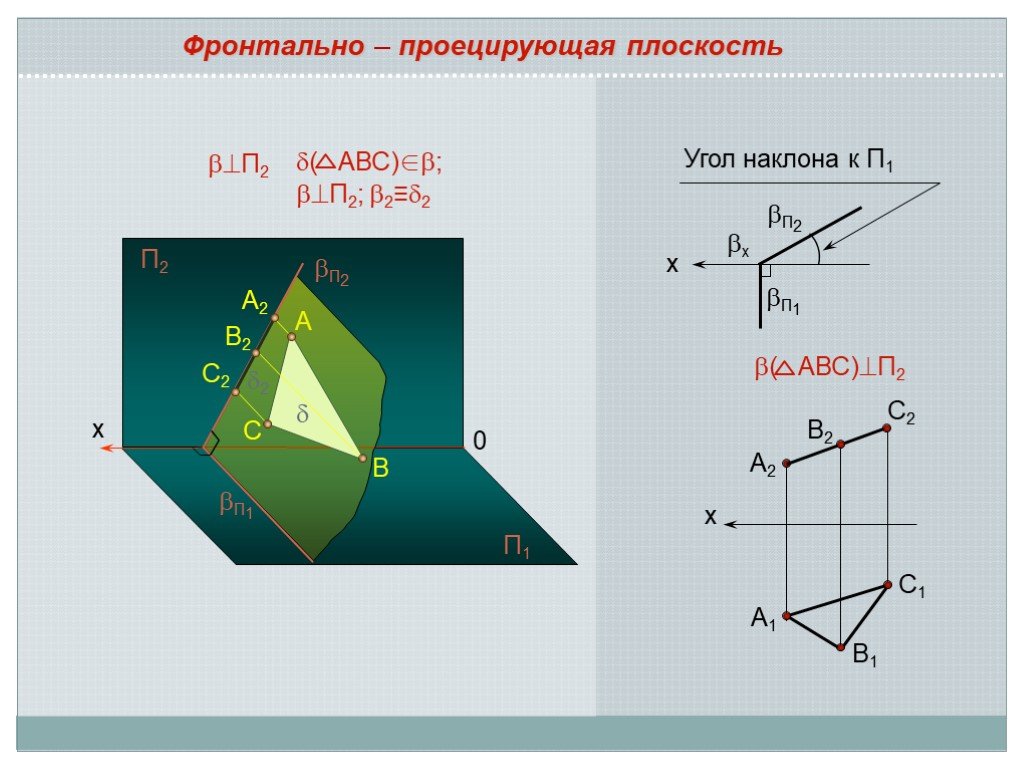
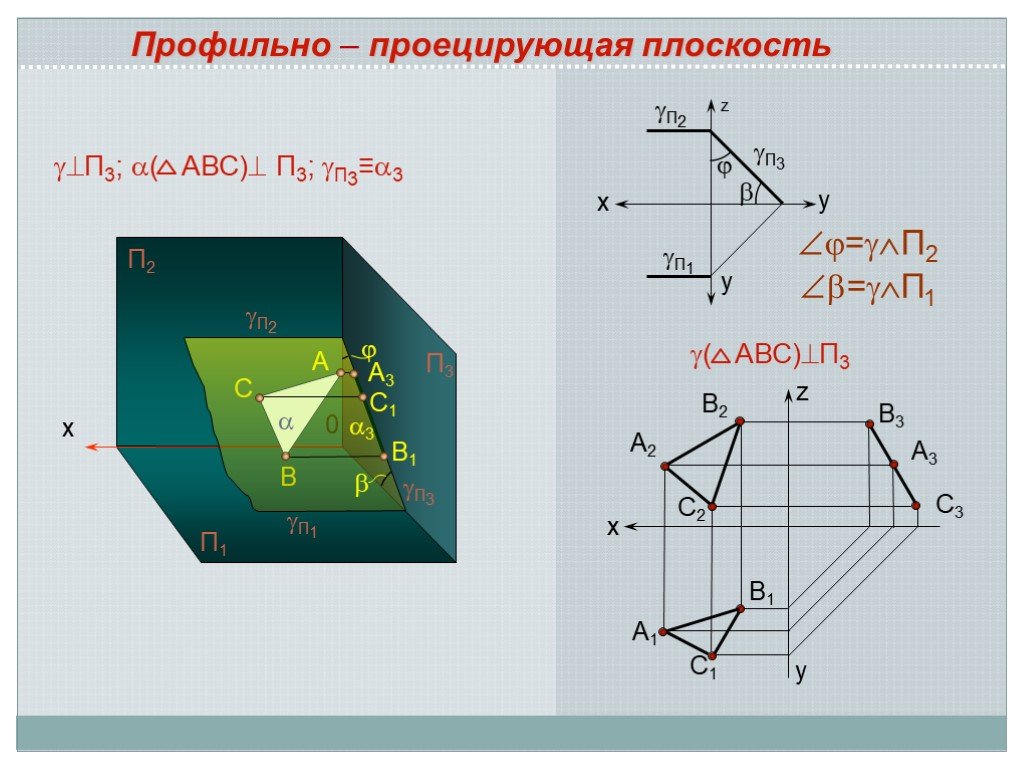
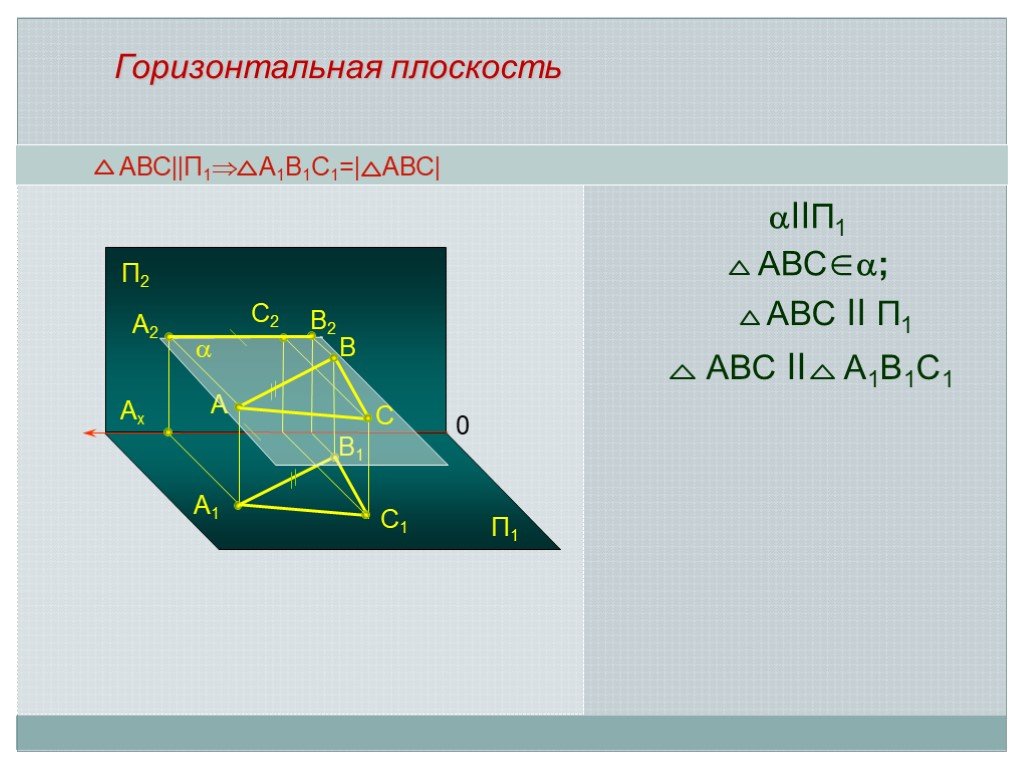
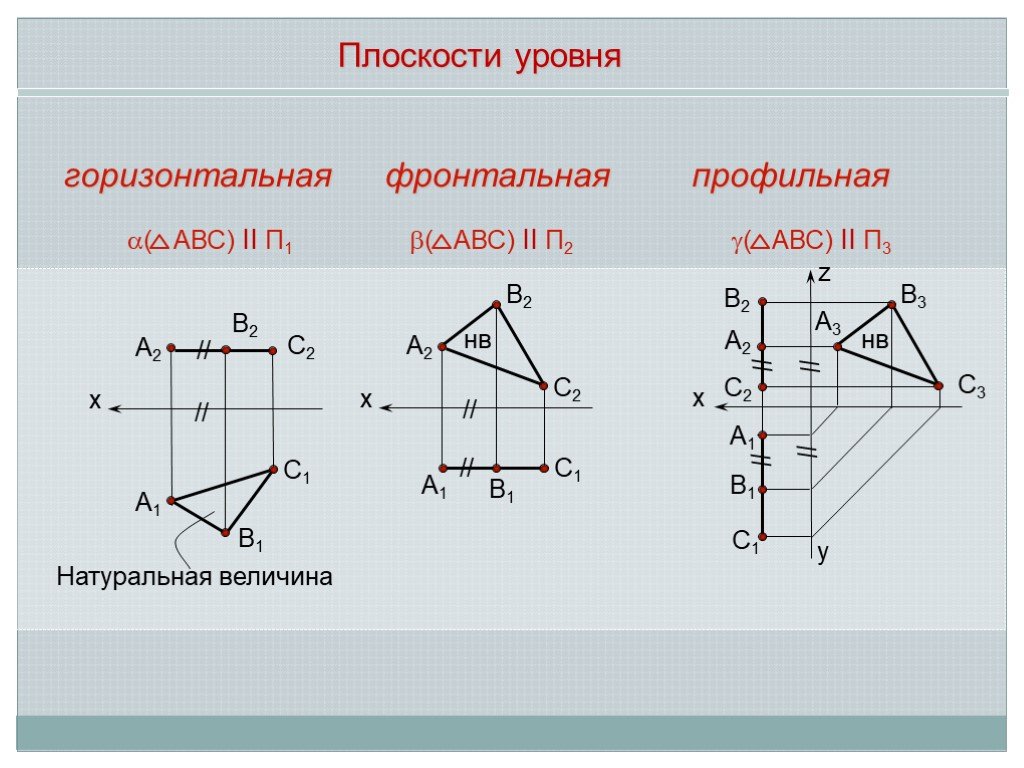
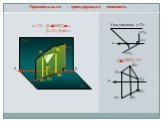
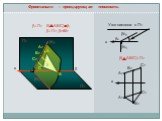
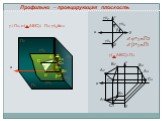
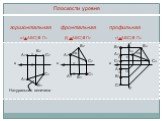
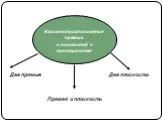
Презентация "Положение плоскости относительно плоскостей проекций" по математике – проект, доклад

Скачать презентацию (0.17 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Презентацию на тему "Положение плоскости относительно плоскостей проекций" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 9 слайд(ов).

Скачать презентацию (0.17 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Положение плоскости относительно плоскостей проекций

Слайд 2

Плоскости частного положения

Слайд 3

Плоскость, перпендикулярная к плоскости проекций, называется проецирующей

Особенности проецирующих плоскостей:

– одна проекция любого элемента, расположенного – в проецирующей плоскости, совпадает с соответствующим следом этой плоскости

– угол наклона заданной плоскости к плоскости проекций на эпюре проецируется в натуральную величину

Проецирующие плоскости

Слайд 4

х А2 В2 С2 С1 А1 В1 ( АВС)П1

Горизонтально – проецирующая плоскость

x П1 x Угол наклона к П2 A1 B1 A 0 B C П2 П2 П1 П1 

( АВС)∈; П1; 1≡ 1

Слайд 5

A2 B2 П2 П1 П2 

( АВС)∈; П2; 2≡2

( АВС)П2 x Угол наклона к П1

Фронтально – проецирующая плоскость

2

Слайд 6

П2 П1 A3 П3  А3 В3 С3 ( АВС)П3

Профильно – проецирующая плоскость

z y П3 у  =П2 =П1 3

П3; ( АВС) П3; П3≡3

Слайд 7

Плоскость, параллельная к плоскости проекций, называется плоскостью уровня

Особенности плоскостей уровня:

Плоскости уровня

– любая плоская фигура, расположенная в плоскости уровня, проецируется на параллельную ей плоскость проекций без искажения, – т.е. в натуральную величину

Слайд 8

АВС||П1 А1В1С1=| АВС|

Ax llП1

Горизонтальная плоскость

АВС∈; АВС ll П1 АВС ll А1В1С1 С

Слайд 9

// ( АВС) ll П1

Натуральная величина

нв ( АВС) ll П2 ( АВС) ll П3 горизонтальная фронтальная профильная

Список похожих презентаций

Взаимное расположение прямых на плоскости

Цели:. Обобщить знания о прямых на плоскости из алгебры и геометрии 7 класса. Выяснить взаимное расположение прямых, заданных уравнением y=kx+b в ...

Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости

Цели урока:. Ввести понятие сферы, шара и их элементов Вывести уравнение сферы в заданной прямоугольной системе координат Рассмотреть возможные случаи ...

Взаимное расположение прямых и плоскостей в пространстве

Взаимное расположение прямых в пространстве. Имеют общую точку лежат в одной плоскости. Не имеют общую точку лежат в одной плоскости. не имеют общую ...

Расположение точек относительно осей координат

Дидактические цели: Формирование аналитического мышления учащихся; Формирование навыков самостоятельной работы. Методические задачи: Познакомиться ...

Проецирование предметов на две и три взаимно перпендикулярные плоскости проекций

Проецирование на одну плоскость. Проецирование на две плоскости. . Проецирование на три плоскости. Найдите соответствие технических рисунков деталей ...

Взаимное расположение прямой и окружности на плоскости

Прямая и окружность пересекаются. d R. d- расстояние от центра окружности до прямой R- радиус окружности. О А В d. Прямая и окружность касаются. d=R. ...

Взаимное расположение прямой и плоскости

1. Прямая принадлежит плоскости. ортогонален нормальному вектору плоскости. И пусть точка. Тогда направляющий вектор прямой. принадлежит прямой. Тогда ...

Прямая на плоскости

Цели и задачи. Цели: Рассмотреть основные понятия по теме «Прямая на плоскости» Задачи: Рассмотреть различные способы задания прямой на плоскости ...

Признак перпендикулярности двух плоскостей

Упражнение 1. Верно ли, что две плоскости, перпендикулярные третьей, параллельны? Ответ: Нет. Упражнение 2. Сколько плоскостей, перпендикулярных данной ...

Построение точки на координатной плоскости

Тема «Построение точки на координатной плоскости». Построить на координатной плоскости точки: М (- 4; 3); А (2 ; -3); Р (0; -2); С (4; 0). х у 0 1 ...

Алгоритмы работы на координатной плоскости

Цели:. Формировать умение работать на координатной плоскости как с положительными, так и отрицательными координатами. Развивать алгоритмическое мышление. ...

Система координат на плоскости

Кто открыл прямоугольную систему координат? Знакомы ли вы с историей возникновения координат? Гиппарх Птолемей Рене Декарт. Что называется системой ...

Векторы на плоскости

Аналитическая геометрия. Алгебраические поверхности и линии на плоскости первого порядка. Опр. Геометрическое место точек в пространстве (на плоскости) ...

В мире плоскостей

1. Изображение. . . . Сколько тут элементов? «Невозможные объекты» и зрительные иллюзии. Бесконечная фотография. Невозможное окно. Сколько здесь колонн? ...

Астрономия на координатной плоскости

Цели урока:. Закрепить полученные знания и навыки. Проявить творчество при изучении данного раздела. Избежать трудностей при изучении темы «Функция» ...

Расстояние от точки до прямой и плоскости

РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ И ПЛОСКОСТЯМИ. Расстоянием между двумя непересекающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного ...

Аксонометрические проекции, получение аксонометрических проекций

НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ. Сколько изображено предметов различной формы? АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ГОСТ 2.317-69. Аксонометрической проекцией называется ...

Рисунок на координатной плоскости

Рене Декарт. Декарт Рене (1596-1650) Рене Декарт родился в последний день марта 1596 года в маленьком городке Лаэ провинции Турень, в не очень знатной, ...

Перпендикулярность прямой и плоскости

Проверка домашней работы. № 127. 1. Доказать: АС перпендикулярна (АМВ). 2. ВМДС – прямоугольник. Доказать: СД перпендикулярна (АВС). 3. АВСД – прямоугольник. ...

Уравнение прямой на плоскости

Уравнение прямой, проходящей через две точки. A(x1; y1) M(x; y) B(x2; y2). Векторы и коллинеарны. Пример. Написать уравнение прямой, проходящей через ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.