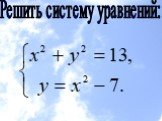Презентация "Системы уравнений" (1 класс) по математике – проект, доклад
Презентацию на тему "Системы уравнений" (1 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение системы линейных уравнений методом Крамера
Системы линейных уравнений. Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных. ...Решение задач системы уравнений
Цель : закрепление и углубление знаний и умений решения задач. Задачи : *развитие мыслительных способностей, *развитие познавательного интереса, * ...Решение неполных квадратных уравнений
ПРОБЛЕМА. Решение неполных квадратных уравнений нерациональным способом. Изучив данную тему в 8 классе, учащиеся в старших классах забывают и порой ...Решение показательных уравнений
1 3 4. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ. Уравнения вида af(x)=ag(x),где a - положительное число , отличное от 1,и уравнения , сводящиеся к этому виду , называются ...Решение квадратных уравнений различными способами
Герберт Спенсер, английский философ, когда-то сказал: “Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются ...Решение линейных уравнений, содержащих неизвестное под знаком модуля
ЦЕЛЬ РАБОТЫ. Рассмотреть примеры уравнений, содержащих неизвестное под знаком модуля с точки зрения геометрического смысла модуля и алгебраического ...Решение уравнений
Тема урока: Решение уравнений ( повторение). Цель урока : повторить правила раскрытия скобок, приведение подобных слагаемых, общую схему решения линейных ...Решение иррациональных уравнений
В данной работе рассматриваются иррациональные уравнения, а также приёмы их решения, которые будут полезны любым ученикам, особенно для подготовки ...Галактика формул и уравнений
« Галактика формул и уравнений». Цели урока:. закрепить буквенную запись формул сокращенного умножении и их словесные формулировок закрепить и усовершенствовать ...Решение тригонометрических уравнений
Цели урока:. Создания условий для осознанного усвоения решения тригонометрических уравнений вида a sinx + b cosx = c. Формирование навыков самоконтроля ...Виды показательных уравнений
Показательным уравнением называется уравнение, в котором неизвестное (x) входит только в показатели степени при некоторых постоянных основаниях. Для ...Виды показательных уравнений и способы их решения
Умные мысли. Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует для данного ...Виды квадратных уравнений
гипотеза. Каждый человек, особенно если он ученик 8 класса, может решить квадратное уравнение, если знает ответы на вопросы…. вопросы... Определение ...В мире квадратных уравнений
Оглавление. Введение Заметки прошлого Основные понятия Теорема Виета Способы решения квадратного уравнения. Математика — основа точных наук. На первый ...Аналитический и численный методы решения систем уравнений с параметром
АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...Решение рациональных уравнений
Теоретический тест: Действия с алгебраическими дробями. 2. Основное свойство алгебраической дроби:. а) И числитель, и знаменатель дроби можно умножить ...Графический метод решения систем уравнений с двумя переменными
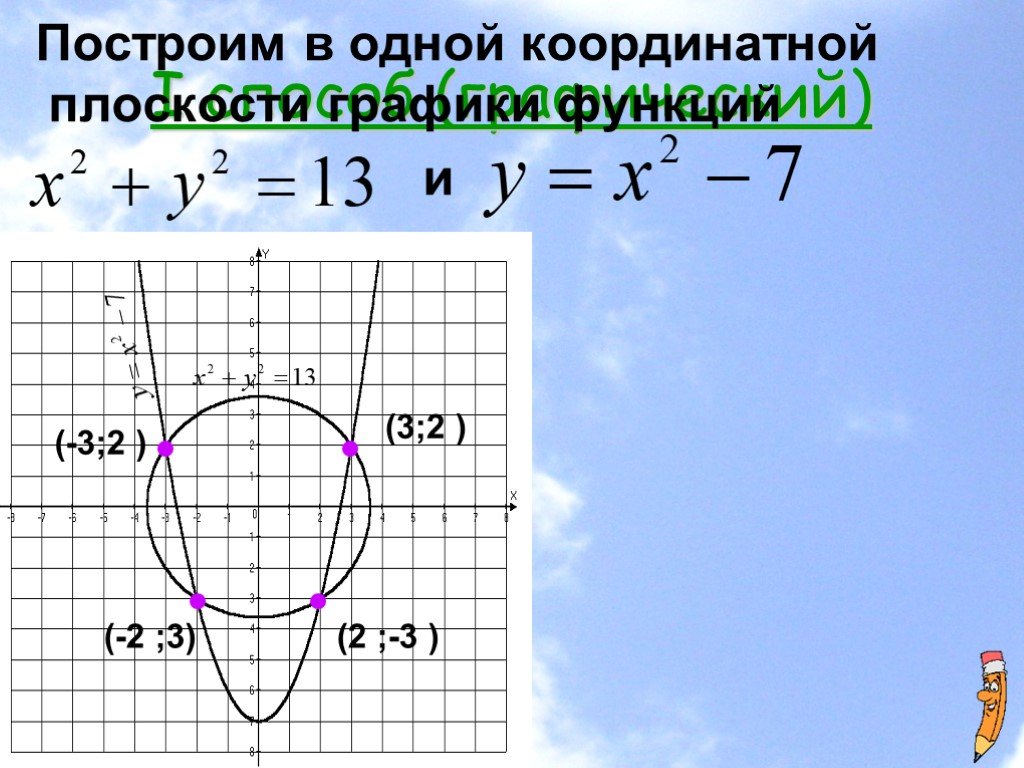
Обобщить графический способ решения систем уравнений; Сформировать умения графи-чески решать системы уравне-ний второй степени, привлекая известные ...Решение систем рациональных уравнений графическим способом
Устная работа:. Каким уравнением задаётся данный график? А. (х+2)2+(у-2)2=4 Б. (х-2)2+у2=4 В. (х-2)2+у2=16 Г. (х-2)2+у2=2. А. у=-х2+2 Б. у=х2 +2 В. ...Графический способ решения квадратных уравнений
Графический способ решения уравнений. Решить графически уравнение. Ответ: х=-3 или х=1. Самостоятельная работа. 1. Постройте график функции и укажите ...Решение уравнений
Неслучайно известный немецкий ученый-математик Карл Фридрих Гаусс однажды сказал, что «математика – царица наук», которая безраздельно властвует над ...Конспекты
Задачи, решаемые составлением системы уравнений
9 класс алгебра. Тема урока. : « Задачи, решаемые составлением системы уравнений». Учебно-воспитательные задачи:. 1). Сформировать модель алгоритма ...Решение задач составлением системы уравнений
Муниципальное общеобразовательное учреждение общеобразовательная школа №53. пос. Октябрьский Люберецкий район Московская область. . . ...Решение квадратных уравнений
Урок для 8 класса по теме «Решение квадратных уравнений». . Цели урока:. образовательные. : обобщение и систематизация основных знаний и умений ...Решение квадратных уравнений
. План-конспект урока по математике в 8 классе малокомплектной школы. . Тема урока. : Решение квадратных уравнений. Место урока в учебном ...Решение задач с помощью уравнений
Отдел образования администрации Тальменского района Алтайского края. МКОУ «Новоозёрская СОШ». План урока математики в 5 классе по теме:. ...Решение рациональных уравнений
9 класс. Тема. : Решение рациональных уравнений. Цель. :. . 1. Обобщить, углубить знания учащихся по решению рациональных уравнений. 2. Способствовать ...Решение показательных уравнений
Государственное бюджетное образовательное учреждение. Центр образования №170 Санкт-Петербурга. План-конспект двух уроков по алгебре и ...Решение логарифмических уравнений
Государственное бюджетное образовательное учреждение. . среднего профессионального образования. Пермский политехнический колледж имени Н.Г.Славянова. ...Графический способ решения система уравнений с двумя переменными
Урок алгебры в10 классе по теме: «Графический способ решения система уравнений с двумя переменными». Цель урока:. добиться усвоения учащимися смысла ...Графический способ решения систем уравнений
Тема урока:. . Графический способ решения систем уравнений. Тип урока. : Урок изучения нового материала. Цели урока. :. Образовательные. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:4 мая 2019
Категория:Математика
Классы:
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию