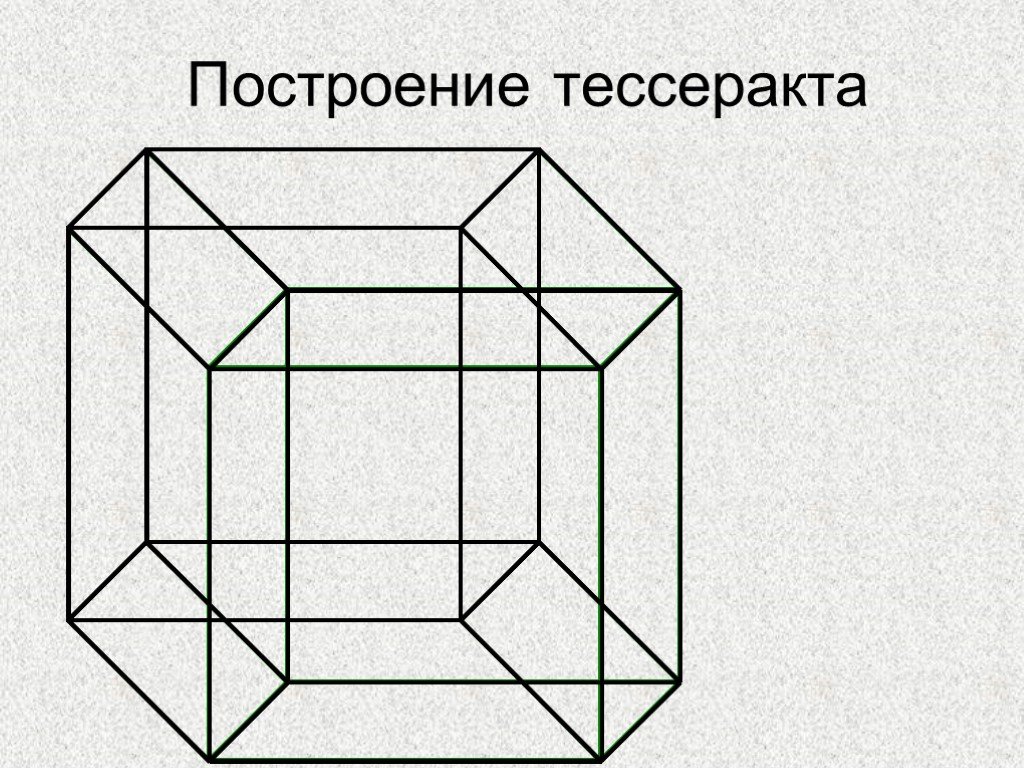
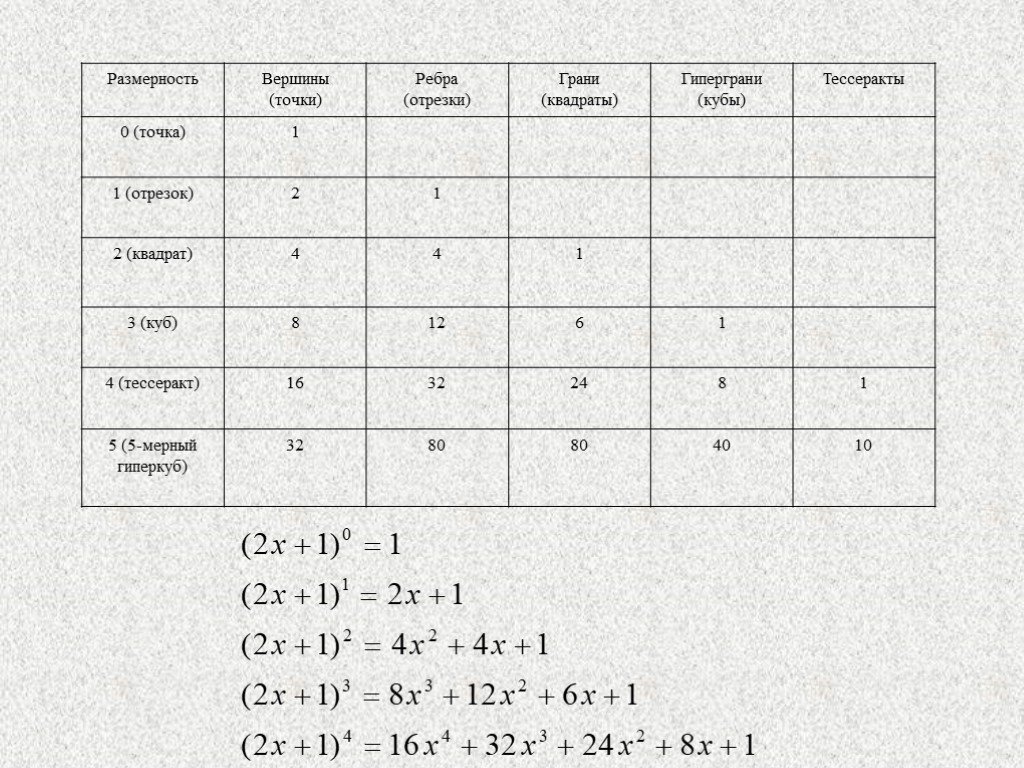
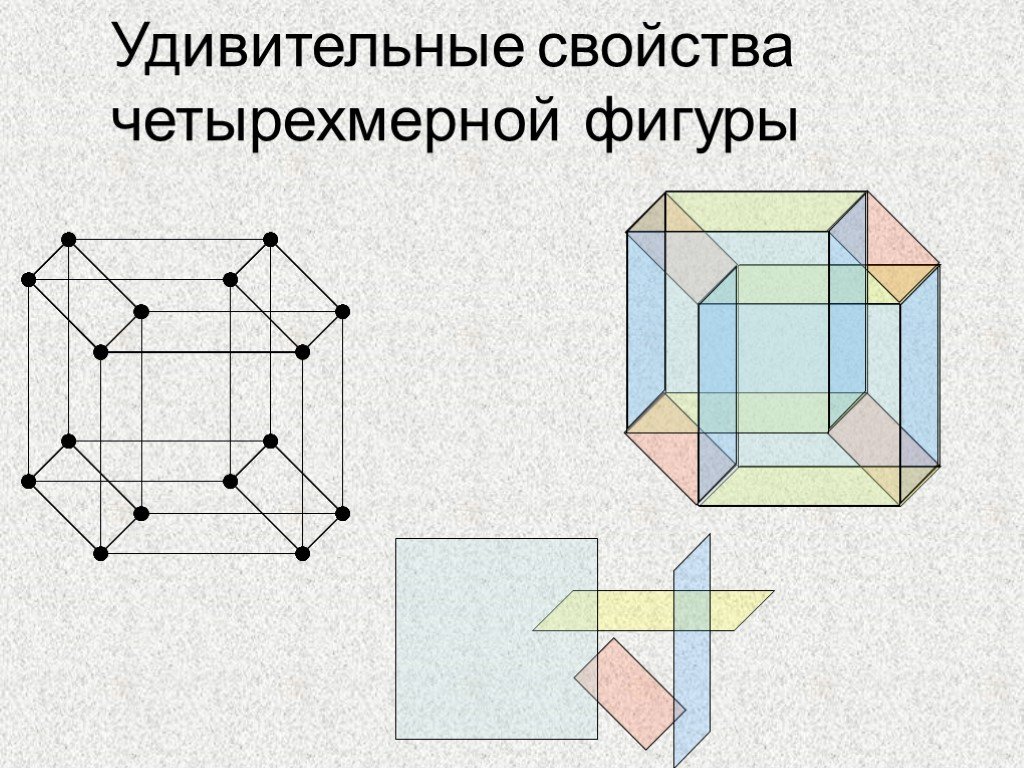
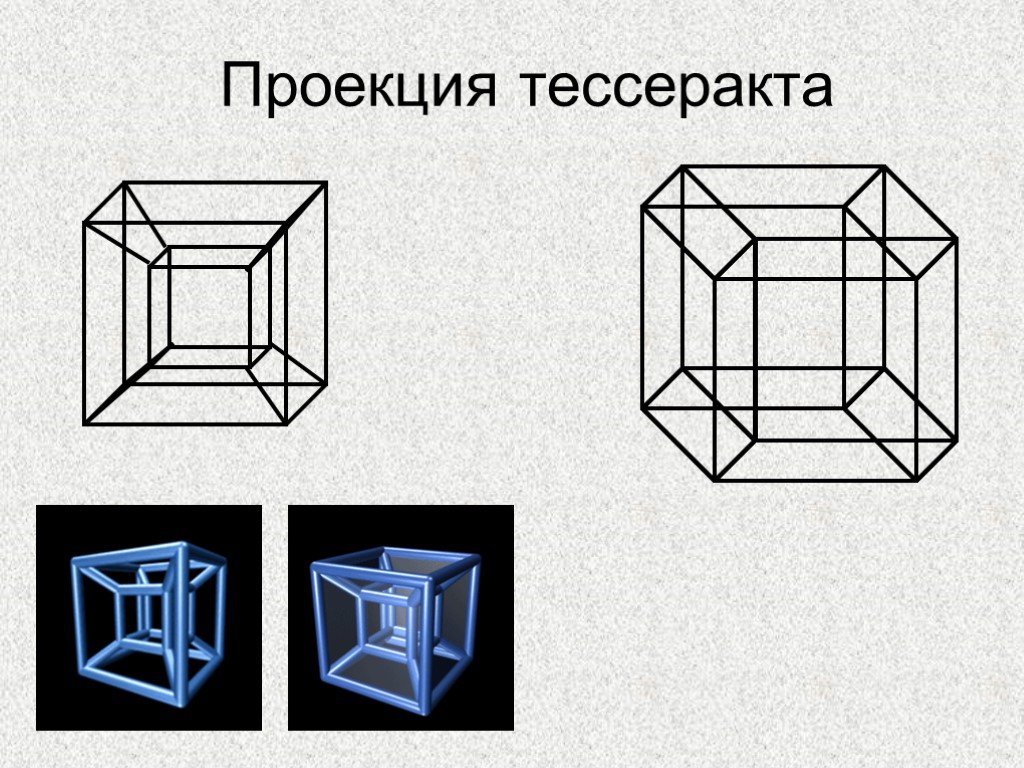
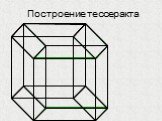
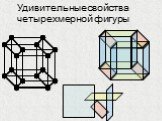
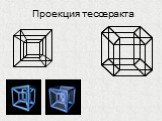
Презентация "Построение гиперкуба" по математике – проект, доклад
Презентацию на тему "Построение гиперкуба" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
Слайды презентации
Список похожих презентаций
Построение треугольника по трем элементам
Построение треугольника по трем элементам. 1 вариант - построение треугольника по двум сторонам и углу между ними. 2 вариант - построение треугольника ...Построение сечений: метод следа
Существует три основных метода построения сечений многогранников: Метод следов. Метод вспомогательных сечений. Комбинированный метод. Метод следов ...Построение точек по заданным координатам
Эталон для самопроверки домашнего задания: Стр. 56, № 10 36 : 2 . 3 = 54 (км/ч) скорость второго грузовика; 36 + 54 = 90 (км/ч) скорость сближения ...Построение сечений многогранников
В работе над проектом принимали участие ученики 9 класса ГОУ СОШ «Школа здоровья» №198 г. Москвы. Пономарёв Руслан Нелюбова Татьяна. Колотикова Дарина. ...Построение сечений многогранников методом «следа»
Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть точки данного многогранника. Сечением многогранника называется ...Построение правильных многоугольников
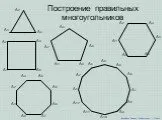
В заданиях на построение используются: карандаш, линейка(для проведения прямых, лучей и отрезков) и циркуль(для построения окружностей и дуг). I. ...Построение сечений многогранника
Содержание. Определение. Примеры построений сечений. Задания на построение сечений. Определение. Если пересечением многогранника и плоскости является ...Построение геометрических тел
Проверь свое пространственное мышление. Принадлежит ли пара изображений одному и тому же кубику? . Найди соответствие букв и цифр. Цилиндры Призмы. ...Построение геометрических тел
Пирамида Призма S. Проекция геометрических тел на плоскость. В куб вписан октаэдр. F A D C B E. ...Построение арифметических выражений
Арифметическое выражение может включать константы, переменные, функции, скобки, знаки. Приоритет: унарный минус *, /, div, mod +, - Порядок действий ...Построение биссектрис треугольника
Чертим треугольник. В С А. Строим биссектрису угла А. D н X Z. Строим биссектрису угла В. Е k. Строим биссектрису угла C. s F. Точка О – точка пересечения ...Построение аксонометрических проекций
-1- Способ построения «от формообразующей плоскости». Чертёж предмета в системе прямоугольных проекций. 0 X Z Y. Этапы построения аксонометрических ...Пирамида. Построение пирамиды и её плоских сечений. Усечённая пирамида. Правильная пирамида.
Что такое пирамида? Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.), а остальные ...Периметр треугольника. Построение треугольника по заданным сторонам
1.Классификация треугольников по длинам сторон. Равносторонний треугольник. 4 см 4см. Разносторонний треугольник. 5см 6 см 7 см. Равнобедренный треугольник. ...Построение циркулем и линейкой
Цели урока:. Рассмотреть новый класс задач на построение; Рассмотреть примеры задач на построение; Научиться решать такие задачи. Оцени себя! Верные ...Построение геометрических фракталов методом рекурсии
"Почему геометрию часто называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, дерева или берега моря. ...Моделирование в стереометрии Построение сечений
Теорема:. Если две непараллельные прямые, принадлежащие одной плоскости, пересекают прямую, не лежащую в этой плоскости, то все три прямые пересекаются ...Построение графика квадратичной функции
Сдвиг графика функции y = ax2 вдоль оси y. y = x2 y = x2+1 x y. -2 1 0 y = x2 – 2. Сдвиг графика функции y = ax2 вдоль оси x. -3 y = (x+3)2. 2 y = ...Построение равнобедренного треугольника
Задача. Условие: Построить ABC по стороне АС=4см и углу при основании. Дано: АС=4 см Угол α А С А. Построение. Построение: 1) Построить прямую a 2)AC ...Построение графика квадратичной функции
Цели:. Формирование у учащихся умения строить график квадратичной функции в соответствии со схемой. определение. Квадратичной функцией называется ...Конспекты
Построение сечения тетраэдра и параллелепипеда
Методическая разработка урока. Дата проведения урока. . . 10 класс. Тема урока: «Построение сечения тетраэдра и параллелепипеда». Тип урок: ...Построение треугольника по трем элементам
Муниципальное бюджетное общеобразовательное учреждение. «Истимисская средняя образовательная школа». Ключевского района. Алтайского края. ...Построение сечений многогранников
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 1 им. Гриши Акулова. . г.Донецка, Ростовской области. ...Построение сечений многогранников на основе аксиоматики
Чудаева Елена Владимировна, учитель математики,. МОУ «Инсарская средняя общеобразовательная школа №1»,. г. Инсар, Республика Мордовия. . Автор. ...Построение правильных многоугольников
Открытый урок по геометрии в 9 классе(в рамках ФГОС). Учитель 1 кв. категории - Савченко Мария Анатольевна. МАОУ «Молчановская СОШ № 2» Молчановского ...Построение сечений
Шарова Елена Владимировна. Учитель математики. Муниципального общеобразовательного учреждения Усвятская средняя общеобразовательная школа. Номинация: ...Построение графика квадратичной функции
Открытый урок по алгебре 8 класс. «Построение графика квадратичной функции». учителя ГОУ центра образования № 671 «Перспектива» Санкт-Петербурга. ...Построение отрезков
Урок математики 1 класс. Тема: Построение отрезков. . . Тип урока. : изучение нового материала. . Цель урока:. формировать умение чертить ...Построение графика квадратичной функции
ПЛАН-КОНСПЕКТ УРОКА Построение графика квадратичной функции. . ФИО (полностью). . Мурадова О.Р. . . . Место работы. . ...Построение графика квадратичной функции
Учитель: Рогачева Татьяна Викторовна. Место работы: ГОУ СОШ №103, Санкт-Петербург. Должность: Учитель математики. Урок алгебры в 9 классе. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 апреля 2019
Категория:Математика
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию