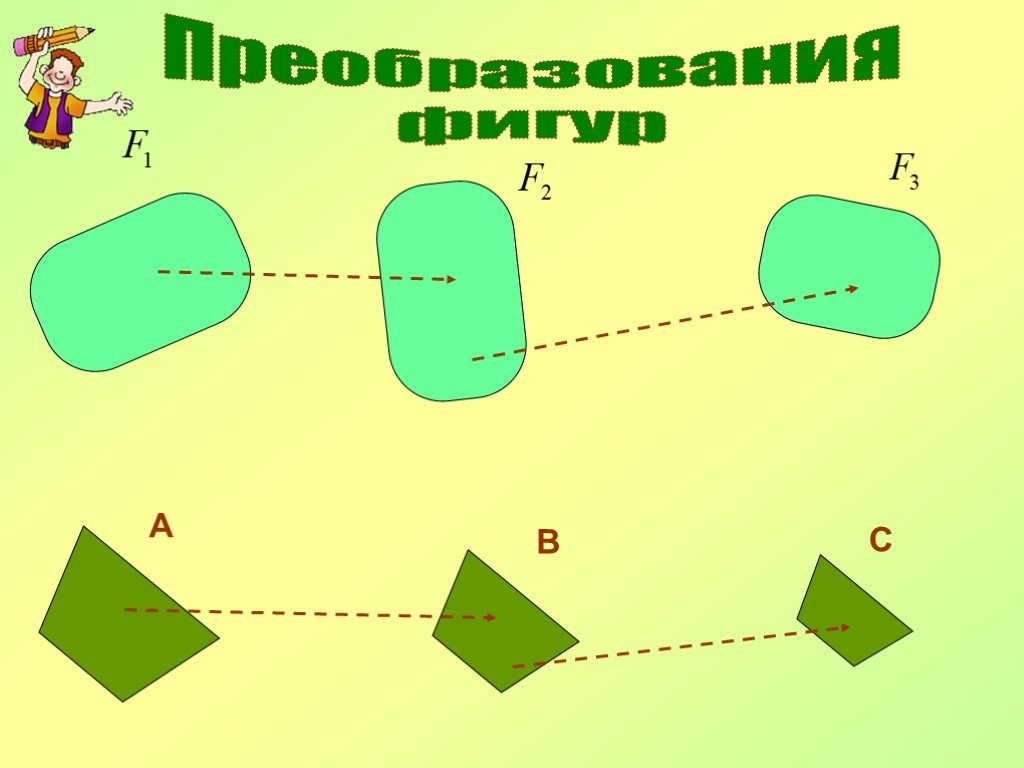
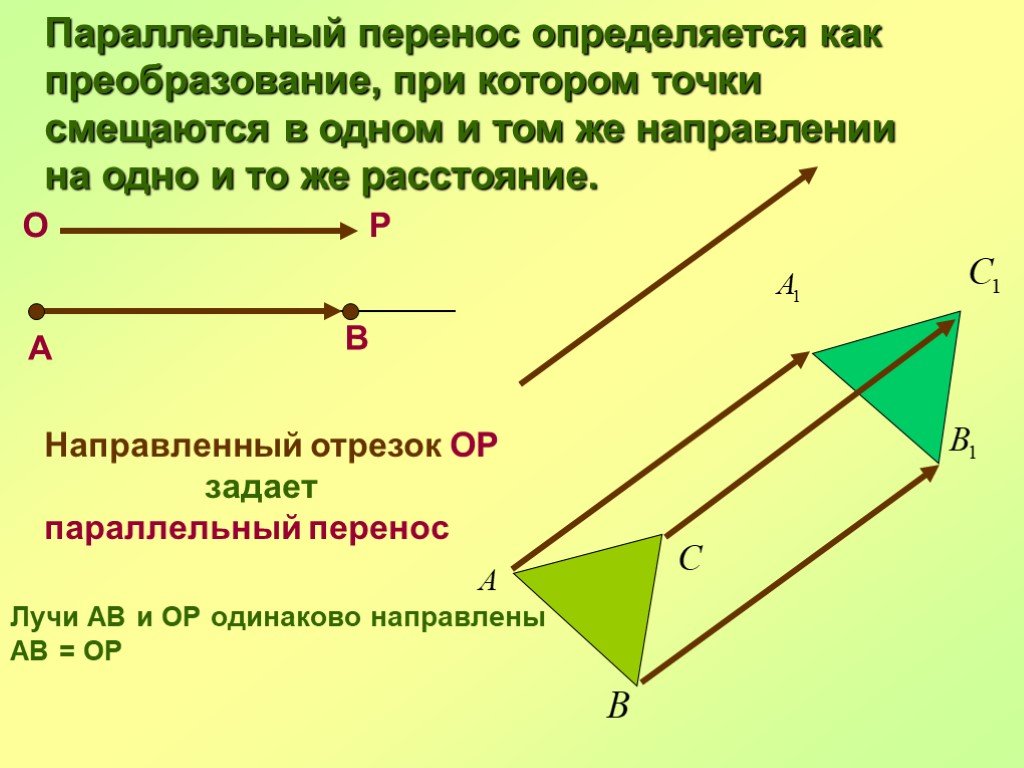
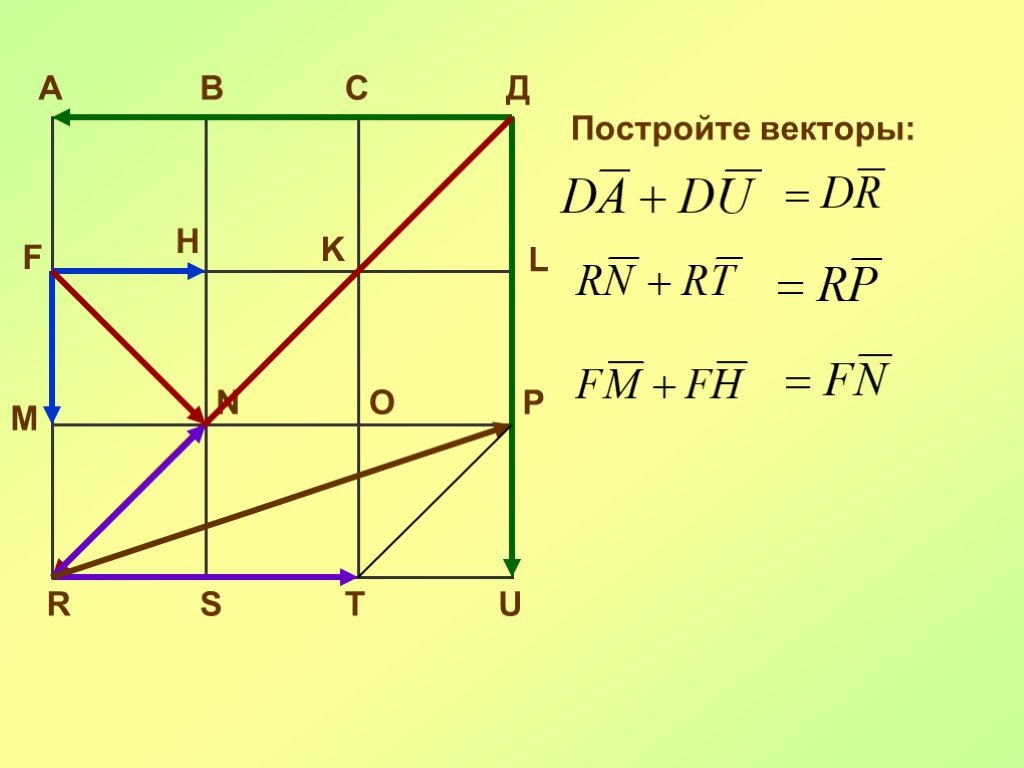
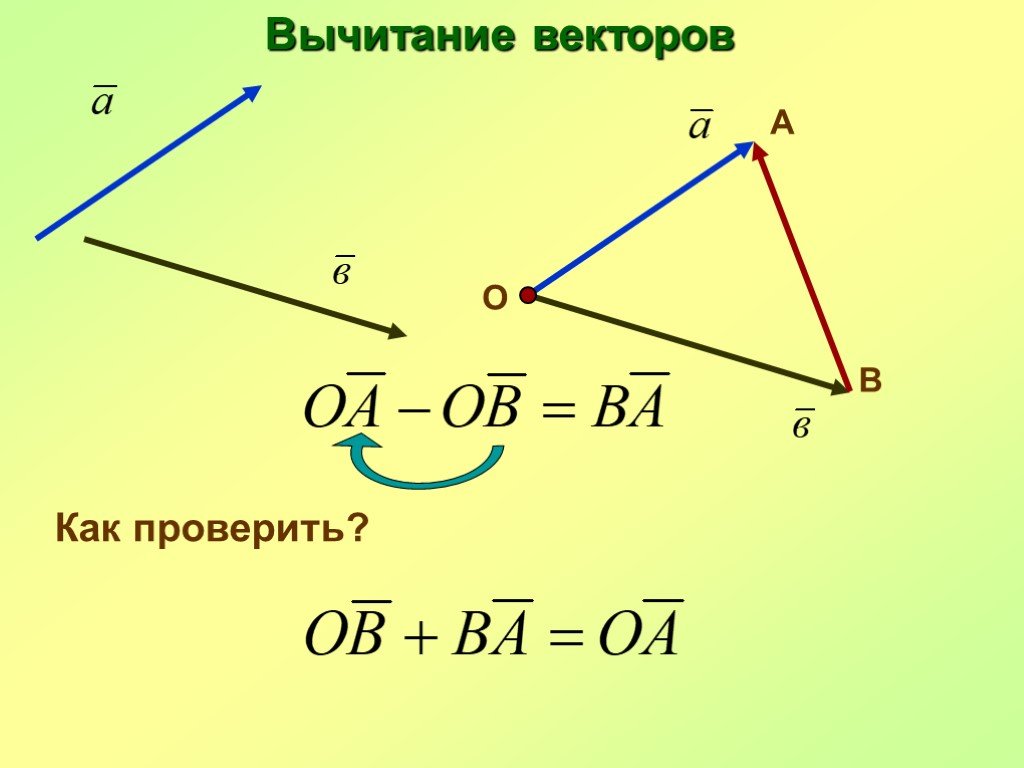
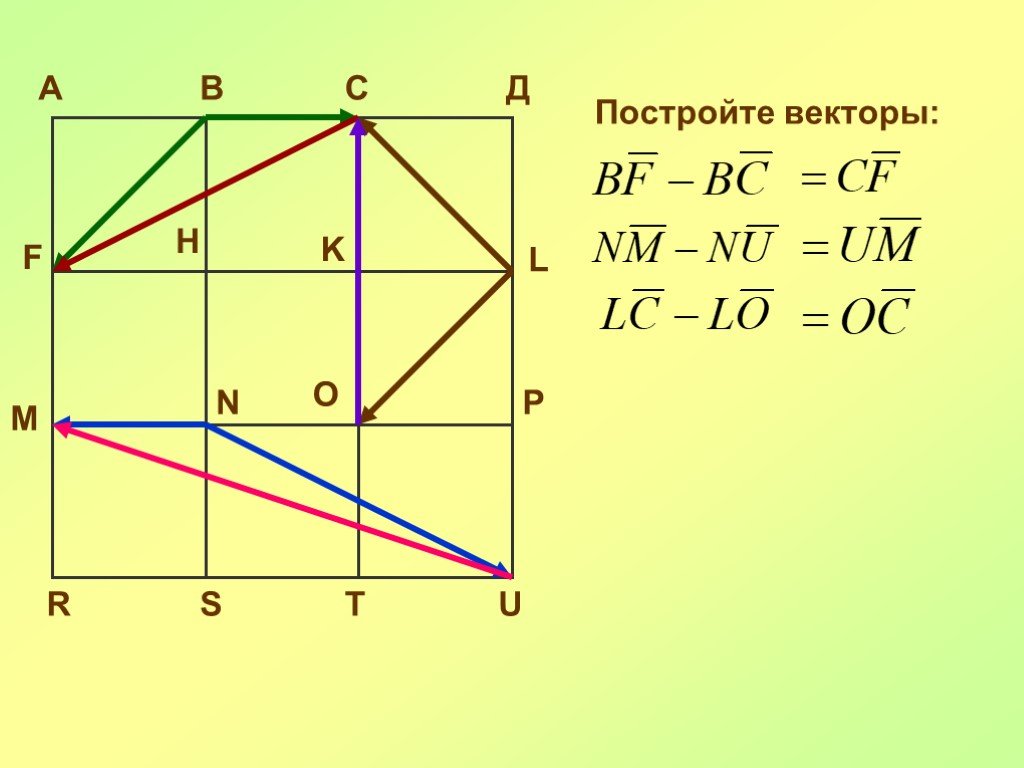
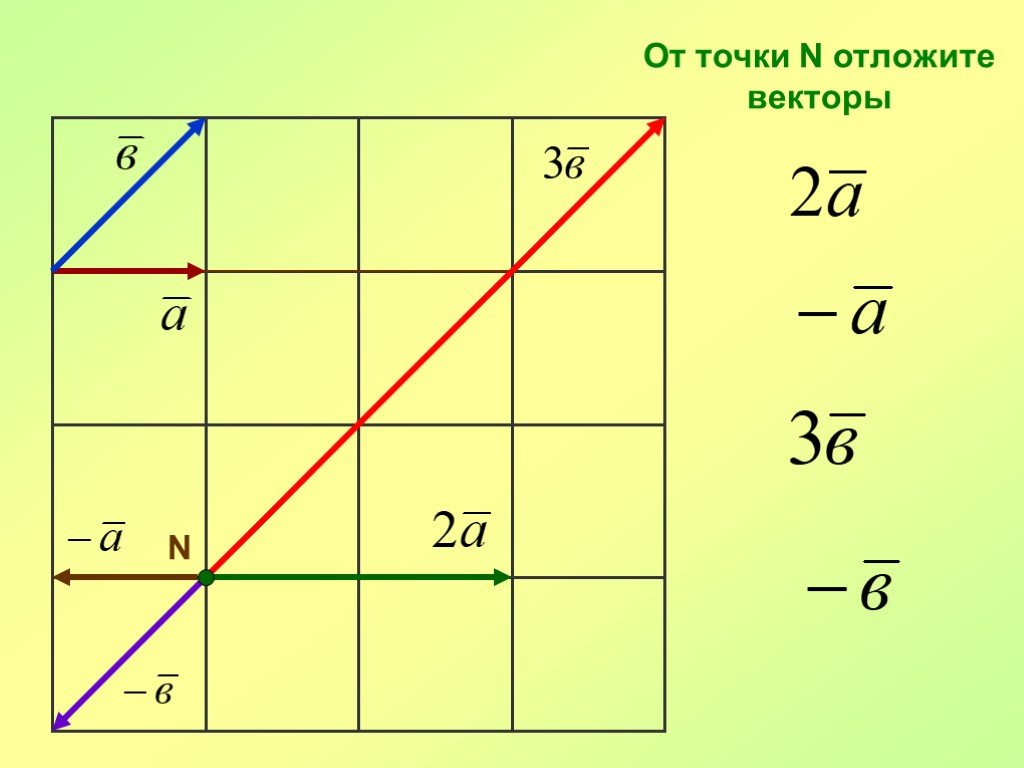
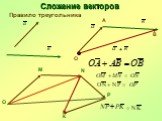
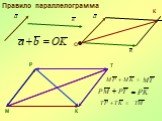
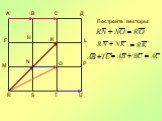
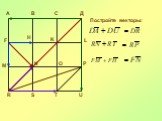
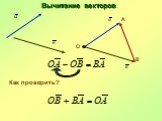
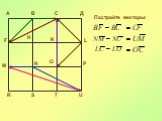
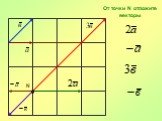
Презентация "Преобразования фигур. Движение. Векторы, действия с векторами" по математике – проект, доклад

Темы презентации: Движение. Преобразования фигур. Симметрия относительно точки. Симметрия относительно прямой. Поворот. Параллельный перенос. 2. Векторы. Сложение, вычитание векторов. Умножение вектора на число. Решение задач. Материал изложен в соответствии с учебником «Геометрия 7-9» А.В.Погорелов. Слайды № 9,11, 13, 16, 17 демонстрируют творческие работы учащихся по заданным темам. Учитель математики Поплавская Марина Борисовна. МОУ «Общеобразовательная средняя школа № 9» г. Рязани

Преобразования фигур

Движение

Уроки геометрии в 8 классе

А В С

Преобразование одной фигуры в другую, при котором сохраняется расстояние между точками называется движением.

.А

Свойства движения

Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.

Следовательно: при движении прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, сохраняются углы между полупрямыми.

Центральная симметрия

Поворот Осевая симметрия

Параллельный перенос

Симметрия относительно точки

О

Точка А симметрична точке В относительно центра симметрии – точки О

Симметрия относительно прямой

а

Точка А симметрична точке В относительно прямой а – оси симметрии

n

О – центр поворота угол АОВ – угол поворота направление поворота – по часовой стрелке

Х

Направление поворота – по часовой стрелке

Преобразование фигуры F, при котором ее произвольная точка (х; у) переходит в точку (х+а; у+в) называется параллельным переносом. Задается формулами

Параллельный перенос задается формулами

В какие точки при этом параллельном переносе переходят точки О(0;0), А(0;4), В(-4;1)?

Р

Направленный отрезок ОР задает параллельный перенос

Лучи АВ и ОР одинаково направлены АВ = ОР

Параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.

Композиция движений

Вектор

Вектор – направленный отрезок. Вектор АВ обозначается

Точка А – начало вектора, точка В – конец вектора.

М Т Д К Н

Назовите векторы, начало и конец вектора.

- одинаково направленные векторы

- противоположно направленные векторы

абсолютная величина (или модуль) вектора – это длина отрезка, изображающего вектор

Назовите одинаково направленные и противоположно направленные векторы

=

Равные векторы одинаково направлены и равны по абсолютной величине

Как от точки отложить вектор, равный данному?

Сложение векторов

Правило треугольника

+ N

Правило параллелограмма

F H K L M O P R S T U

Постройте векторы:

Вычитание векторов

Как проверить?

Умножение вектора на число

и

сонаправленные, если

противоположно направленные, если

От точки N отложите векторы