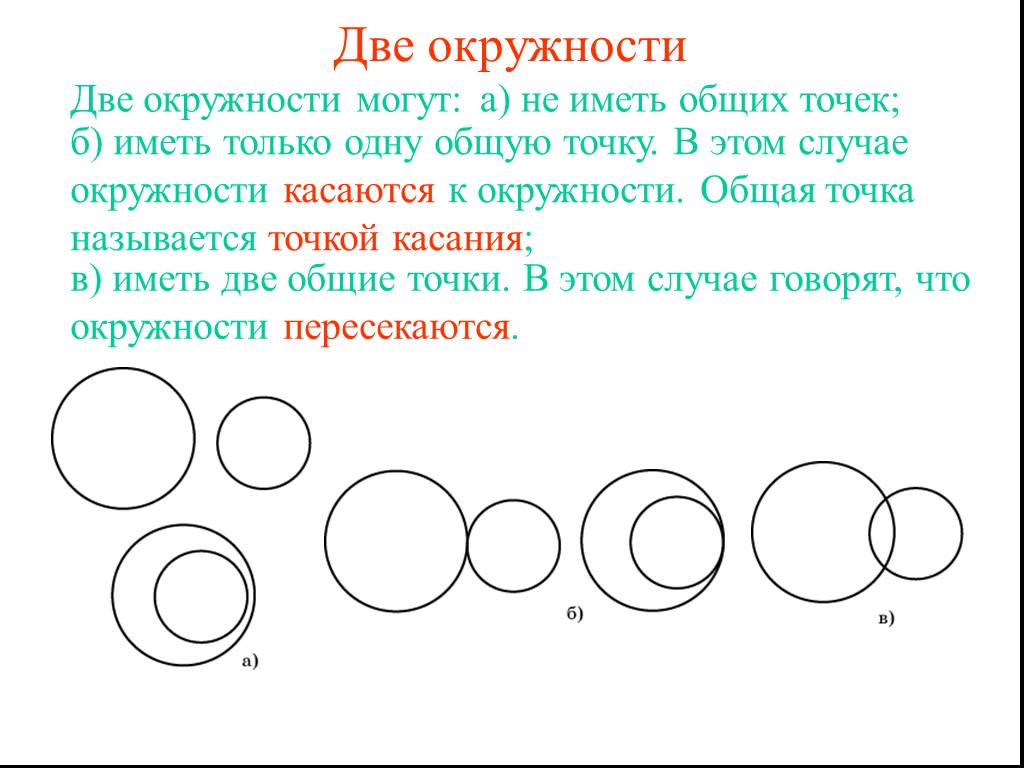
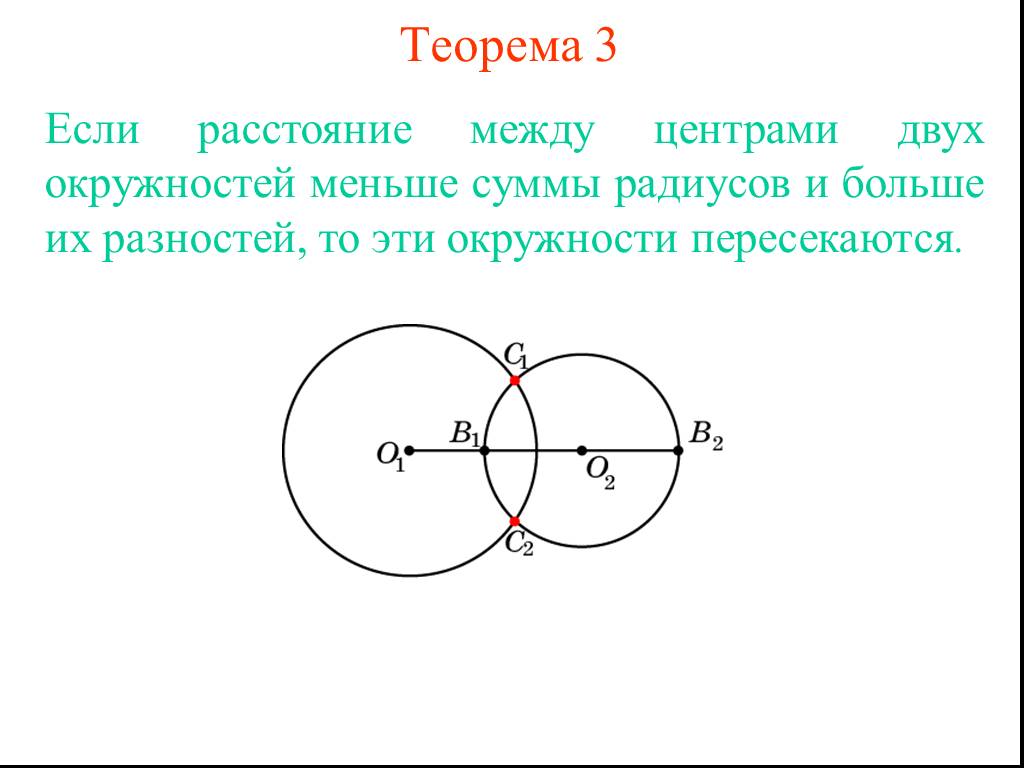
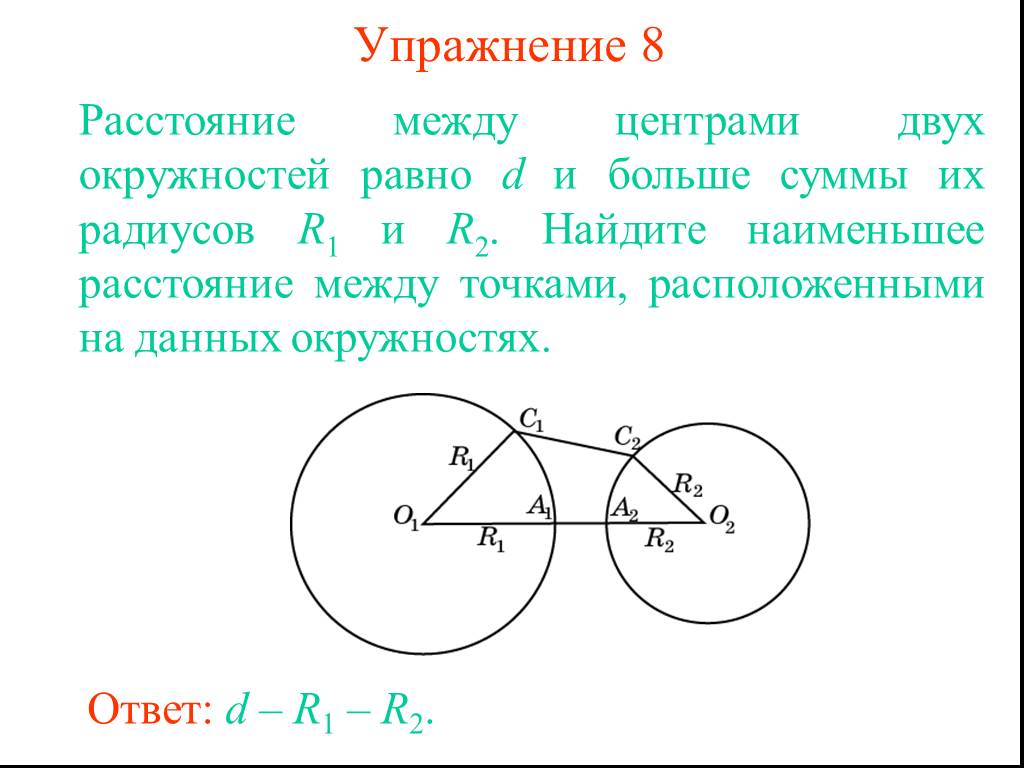
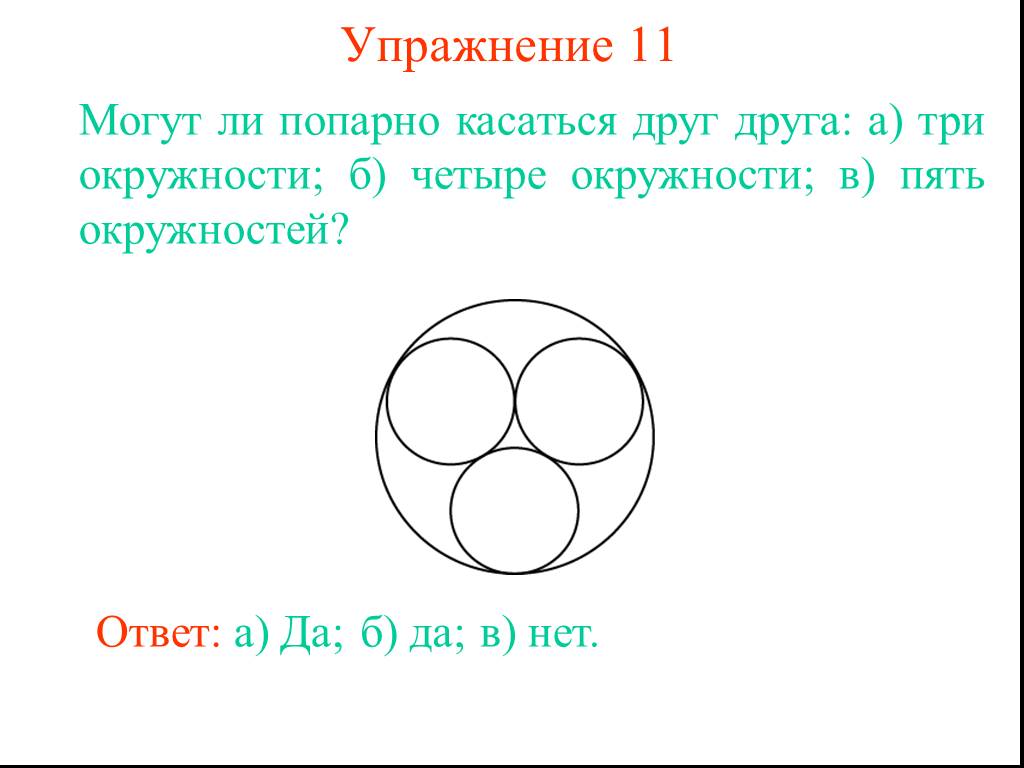
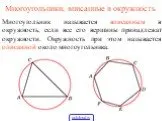
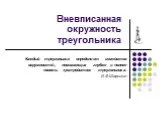
Презентация "Две окружности" по математике – проект, доклад
Презентацию на тему "Две окружности" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 27 слайд(ов).
Слайды презентации
Список похожих презентаций
Касательная к окружности
Дано:. Окружность с центром в точке О радиуса r Прямая, которая не проходит через центр О Расстояние от центра окружности до прямой обозначим буквой ...Использование тригонометрической окружности при решении тригонометрический уравнений
Вычислите устно. Назвать положительный корень уравнения. Найти наименьший положительный корень. . . Найти наибольший отрицательный корень. . . Наибольшее ...Как найти длину окружности
Половина длины окружности единичного радиуса обозначается греческой буквой π. Таким образом, длина окружности единичного радиуса равна 2π. Из рассмотренной ...Зависимость расстояния между точками пересечения прямой и окружности и расстояния от центра окружности до этой прямой
Цель:. Определение зависимости расстояния между точками пересечения прямой и окружности и расстояния от центра окружности до прямой. Задачи:. Рассмотреть ...Задачи по вписанной и описанной окружности
Теорема 1. Около всякого треугольника можно описать окружность. Ее центр является точкой пересечения серединных перпендикуляров к сторонам треугольника. ...Площадь круга. Длина окружности
Тема : Площадь круга. Длина окружности. Цели и задачи: Закрепить основные понятия и определения по данной теме; проверить уровень сформированности ...Формулы описанной и вписанной окружности
1.Устная работа. 1. ОK = 5, АВ = 24. Найти: R. Решение 1) АОВ – равнобедренный, так как АО = ОВ = R, тогда АK = KВ. 2) В АKО, K = 90°. АО = = 13. ...Деление окружности на 4,6 равных частей. Вычерчивание «розетки»
23 января. Классная работа. Диагонали квадрата равны и при пересечении образуют прямые углы. 2. Точка пересечения диагоналей делит их на равные отрезки. ...Деление окружности на 7 равных частей
Пирамиды. Развертки пирамид. 1 2 3 5 6. Найдите правильные развертки пирамид. O R А А/ В. 4 7. Практическая работа. Новогодняя игрушка - подвеска ...Деление окружности
Виды деления окружности:. Деление на 4 и 8 частей. Деление на 3, 6 и 12 частей. Деление на 5 и10 частей. Деление на 7 частей. список литературы:. ...Деление окружности на 3 и 4 части
Деление окружности с помощью циркуля и линейки на 4 части. ...Две прямые, параллельные третьей прямой
Теорема о параллельности трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны. a b с Дано: Доказать: и. Р. Доказать: ...Две замечательные теоремы планеметрии
Цель:. Доказав теоремы Менелая и Чевы, исследовать их применение при решении задач. Задачи:. Показать применение теорем Менелая и Чевы при решении ...Окружающая среда и длина окружности
Dərsin məqsədi. 1. Çevrə və onun mərkəzi 2. Çevrənin radiusu,vətəri və diametri 3. Çevrənin diametri ilə radiusu arasındakı əlaqə 4. Çevrənin uzunluğu ...Деление окружности на равные части
Для меня резинка, братцы, Лютый враг! Не могу я столковаться С ней никак. Сделал я кота и кошку- Красота! А она прошлась немножко- Нет кота! С ней ...Окружность. Длина окружности
Колесо Окружность Центр О R Радиус Диаметр. R - внутренней окружности. R1 - внешней окружности. ? Сначала было замечено, что длина любой окружности ...Длина дуги окружности
3π/4 В С D 0 Ι ΙІ ІІΙ ΙV L = 2πR R = 1, L = 2π ∙ 1 = 2π АС = π АВ = ВС = СD = DA = π/2 π 3π/2 А 5π/4 7π/4 π/4 ●. π/2 4π/3 2π/3 5π/6 7π/6 π/6 11π/6 ...Точки на числовой окружности
. оглавление. Числовая окружность на координатной плоскости Дидактические игры Тригонометр. Литература. Центр числовой окружности совместим. с центром ...Длина окружности
Представим. Что мы разрезаем окружность и «распрямляем» ее в нить. Длина получившегося в этом случае отрезка и есть длина окружности. Длина окружности ...Конспекты
Уравнение окружности
Разработка урока в 9 классе по теме «Уравнение окружности». . Кобзенко Елена Евгеньевна, учитель МОУ СОШ №1 г. Юрюзань Челябинской области. . ...Длина окружности, площадь круга, шар
Алямкина М.А. учитель математики МБОУ «Умётская СОШ » З-Полянского р-на. Тема урока:. Длина окружности, площадь круга, шар. Класс:. . 6. . Предмет:. ...Окружность. Длина окружности
Урок математики в 6 классе по теме. . «Окружность. Длина окружности». Цели:. Образовательная: формировать у учащихся понятие об окружности и ...Длина окружности и площадь круга
Автор Козлова Елена Юрьевна. Учитель математики. Тема урока «Длина окружности и площадь круга». Учебно-методическое обеспечение:. учебник Математика, ...Длина окружности и площадь круга
Зорина Наталья Ивановна,. Учитель математики. МБОУ СОШ№ 40 г.Брянска. Конспект урока по математике в 6 классе с применением ИКТ на тему:. "Длина ...Длина окружности и площадь круга
Государственное специальное (коррекционное). образовательное учреждение школа – интернат №2. ПЛАН-КОНСПЕКТ. Интегрированного ...Длина окружности и площадь круга
1. . . УРОК МАТЕМАТИКИ В 6 КЛАССЕ. УЧЕБНИК «Математика» Н.Я.ВИЛЕНКИН. ТЕМА УРОКА: Длина окружности и площадь круга. ЦЕЛИ И ЗАДАЧИ : Сформировать ...Длина окружности
Муниципальное казённое общеобразовательное учреждение. «Дедиловская средняя общеобразовательная школа» администрации муниципального образования. ...Длина окружности
Технологическая карта урока по теме. «Длина окружности». Раздел курса: Отношения и пропорции. Математика, 6 класс. Учебник: «Математика 6» Н.Я. ...Длина окружности
Технологическая карта урока. Разработчик. : учитель математики ГБОУ СОШ с. Криволучье-Ивановка. Самарской обл., Красноармейского р-она Баранов ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 февраля 2019
Категория:Математика
Содержит:27 слайд(ов)
Поделись с друзьями:
Скачать презентацию