Презентация "Как найти длину окружности" по математике – проект, доклад
Презентацию на тему "Как найти длину окружности" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 29 слайд(ов).
Слайды презентации
Список похожих презентаций
Измеряем длину окружности
Цели урока:. Познакомить учащихся с понятиями: длины окружности одним из вариантов измерения длины окружности числа . Тест. Попробуем измерить длину ...Как найти корни квадратного уравнения?
Привет, восьмиклассник! Твоему вниманию предоставляется проект, который поможет тебе научиться находить корни, квадратных уравнений. Здесь ты найдёшь ...Как найти площадь прямоугольника?
. «Тот , кто не знает математики, не может изучить другие науки и не может познать мир». Роджер Бекон. Зарядка для ума. На какие группы можно разделить ...Как найти число, зная дробь
Цель урока:. обеспечить осознанное усвоение учащимися понятия нахождения части от числа и числа по его части за счет укрупнения дидактической единицы; ...Личинка какого насекомого имеет длину 14 см?
1 3 4. Разложите на множители. е. 2. Не раскладывается. у. _. ь. к. л. ж. н. о. ЖУК-ОЛЕНЬ один из самых больших жуков. Длина самки 28— 45 мм, длина ...Как чётная и нечётная степень влияет на знак числа
Цель: Научиться возводить отрицательное число в степень. Задачи: Выучить правило возведения числа в степень. Научиться применять это правило для решения ...Как построить график функции y=f(x+L)+m, если известен график функции y=f(x)
ТЕМА УРОКА Как построить график функции y=f(x+L)+m, если известен график функции y=f (x). Цель урока: Научиться строить график функции y=f (x + L) ...Как решать неполные квадратные уравнения
Тема урока: Решение неполных квадратных уравнений. Покупка билетов. Вариант – 1. Решить уравнение:. Вариант – 2. Решить уравнение:. Устная работа. ...Как люди научились считать и записывать числа
Цель проекта. Познакомить детей с историей развития понятия числа Пройти и “пережить” весь тот исторический путь, который прошло человечество от операций ...Деление окружности на 3 и 4 части
Деление окружности с помощью циркуля и линейки на 4 части. ...Длина окружности
Мастер подключения презентации к уроку. S T O P. Дальнейший просмотр возможен только при наличии соответствующих знаний. А они у тебя есть? Да. Могу ...Формулы описанной и вписанной окружности
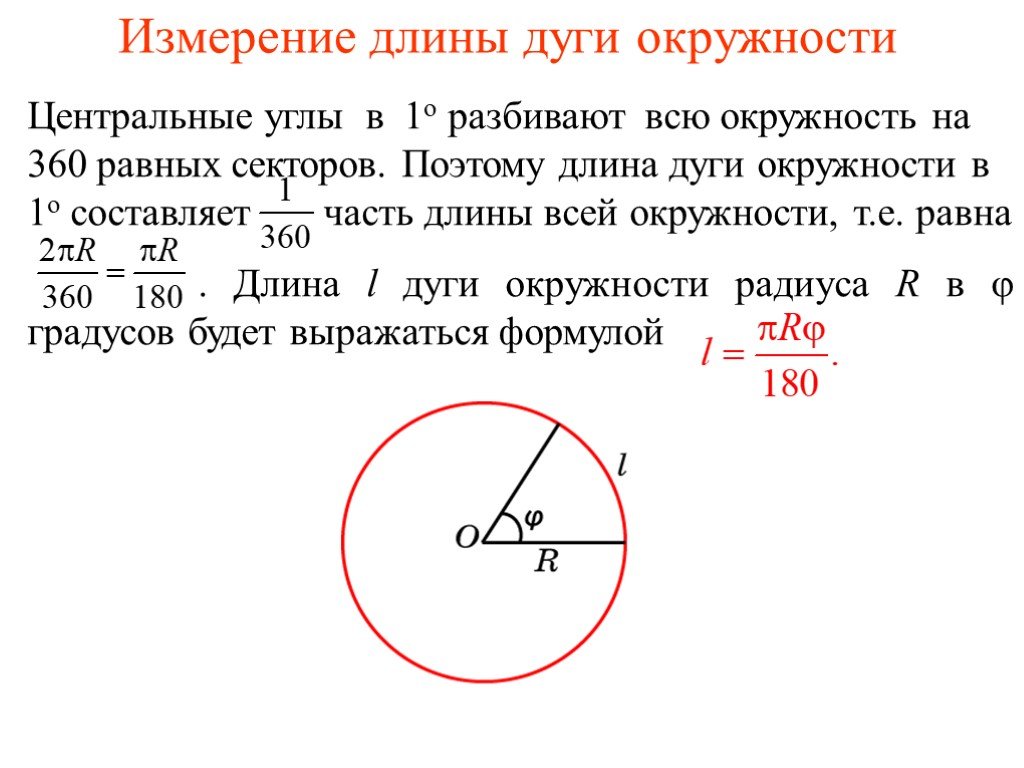
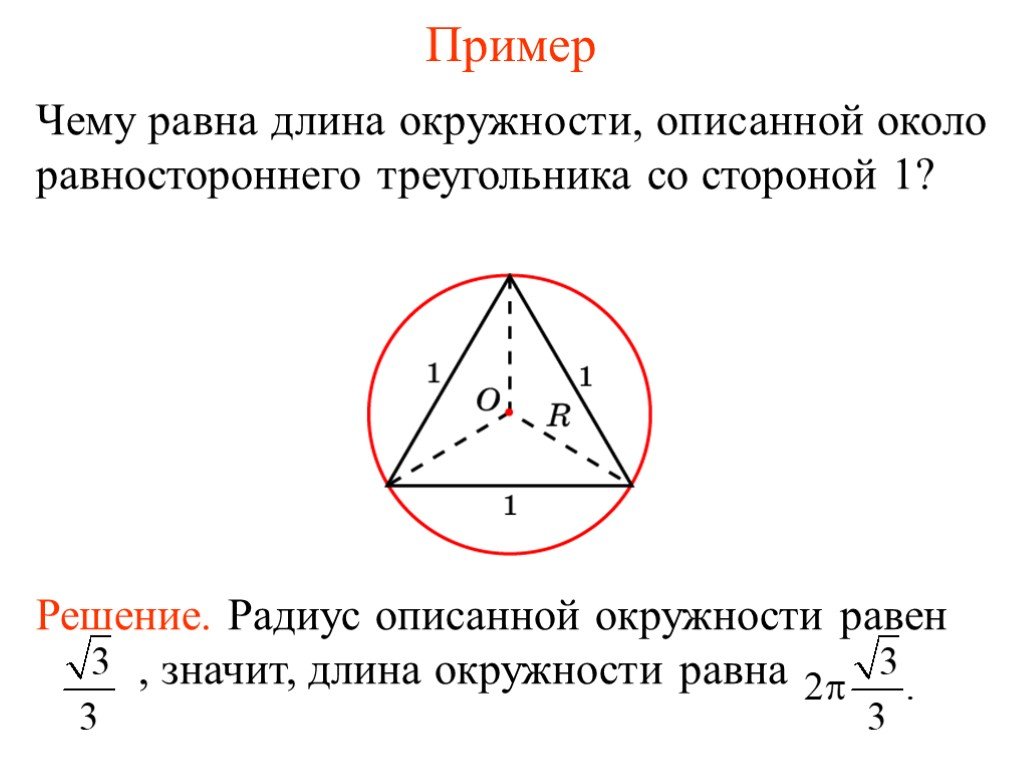
1.Устная работа. 1. ОK = 5, АВ = 24. Найти: R. Решение 1) АОВ – равнобедренный, так как АО = ОВ = R, тогда АK = KВ. 2) В АKО, K = 90°. АО = = 13. ...Длина дуги окружности
3π/4 В С D 0 Ι ΙІ ІІΙ ΙV L = 2πR R = 1, L = 2π ∙ 1 = 2π АС = π АВ = ВС = СD = DA = π/2 π 3π/2 А 5π/4 7π/4 π/4 ●. π/2 4π/3 2π/3 5π/6 7π/6 π/6 11π/6 ...Длина окружности
Представим. Что мы разрезаем окружность и «распрямляем» ее в нить. Длина получившегося в этом случае отрезка и есть длина окружности. Длина окружности ...Деление окружности на равные части
Для меня резинка, братцы, Лютый враг! Не могу я столковаться С ней никак. Сделал я кота и кошку- Красота! А она прошлась немножко- Нет кота! С ней ...Деление окружности на 7 равных частей
Пирамиды. Развертки пирамид. 1 2 3 5 6. Найдите правильные развертки пирамид. O R А А/ В. 4 7. Практическая работа. Новогодняя игрушка - подвеска ...Деление окружности на 4,6 равных частей. Вычерчивание «розетки»
23 января. Классная работа. Диагонали квадрата равны и при пересечении образуют прямые углы. 2. Точка пересечения диагоналей делит их на равные отрезки. ...Окружность, длина окружности
диаметр Окружность центр R D O радиус. Окружность. Длина окружности. А В С D = 2R R = D : 2. Заполните таблицу:. 2,7 5,6 18 11 1 5 8 1 2 5,4 2,8 9 ...Длина окружности
Цели урока. Образовательная: вывести формулу длины окружности и научить применять ее при решении текстовых задач Развивающая: развитие речи учащихся, ...Помоги Барашку найти правильный ответ
Помоги Барашку найти правильный ответ: 10 – 8 + 3 =. 5 7. 9 – 2 + 3 = 6 10. 6 + 3 – 4 = 2. 3 + 3 – 4 =. 5 + 4 – 4 =. 7 - 2 – 4 = 3 1. 1 + 3 – 2 =. ...Конспекты
Как найти часть от целого и целое по его части
Открытый урок по математике в 5б классе. Учитель: Бамбутова М.И. Тема: Как найти часть от целого и целое по его части. Цель: учиться решать задачи ...Измеряем длину в сантиметрах
ПЛАН-КОНСПЕКТ УРОКА. Измеряем длину в сантиметрах. ФИО :. Алексеева Надежда Петровна. . Место работы:. Муниципальное автономное общеобразовательное ...Длина окружности и площадь круга
Зорина Наталья Ивановна,. Учитель математики. МБОУ СОШ№ 40 г.Брянска. Конспект урока по математике в 6 классе с применением ИКТ на тему:. "Длина ...Длина окружности, площадь круга, шар
Алямкина М.А. учитель математики МБОУ «Умётская СОШ » З-Полянского р-на. Тема урока:. Длина окружности, площадь круга, шар. Класс:. . 6. . Предмет:. ...Уравнение окружности
Разработка урока по теме «Уравнение окружности». геометрия 9 класс. Тема урока:. . . Уравнение окружности. Цели:. . Образовательные:. ...Геометрия окружности
Урок математики в 9 классе. учителя МОУ «СОШ № 20» г. Энгельса. Милюткиной Людмилы Николаевны. и учителя математики МОУ «СОШ № 21» г. Энгельса. ...Длина окружности
Технологическая карта урока по теме. «Длина окружности». Раздел курса: Отношения и пропорции. Математика, 6 класс. Учебник: «Математика 6» Н.Я. ...Метрические соотношения в треугольнике и окружности
Тема: Метрические соотношения в треугольнике и окружности. 2чт. Цель: Организовать деятельность учащихся по обобщению и систематизации знаний по ...Длина окружности
Урок математики в 6 классе. по теме: «Длина окружности». Морина Светлана Алексеевна. Муниципальное бюджетное общеобразовательное ...Длина окружности
Муниципальное казённое общеобразовательное учреждение. «Дедиловская средняя общеобразовательная школа» администрации муниципального образования. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 мая 2019
Категория:Математика
Содержит:29 слайд(ов)
Поделись с друзьями:
Скачать презентацию