Презентация "Длина окружности" (9 класс) по математике – проект, доклад
Презентацию на тему "Длина окружности" (9 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Длина окружности. Площадь круга
Устный счёт 500+310 :90 *60 -120 :14 910:13 *8 -80 :160 *350. Отрезки А В С К Круг Цилиндр Окружность Окружность, круг. В С А. Окружность - это замкнутая ...Длина окружности. Площадь круга
Математический словарь:. Правильный многоугольник; Окружность, описанная около правильного многоугольника; Окружность, вписанная в правильный многоугольник; ...Длина окружности
Цели урока. Образовательная: вывести формулу длины окружности и научить применять ее при решении текстовых задач Развивающая: развитие речи учащихся, ...Длина окружности
Окружность Диаметр Радиус О. О – центр окружность. D (d) – диаметр R (r) – радиус D = 2R. Диаметр d= 5м. Длина окружности – С ? Задача: Цветочная ...Длина окружности
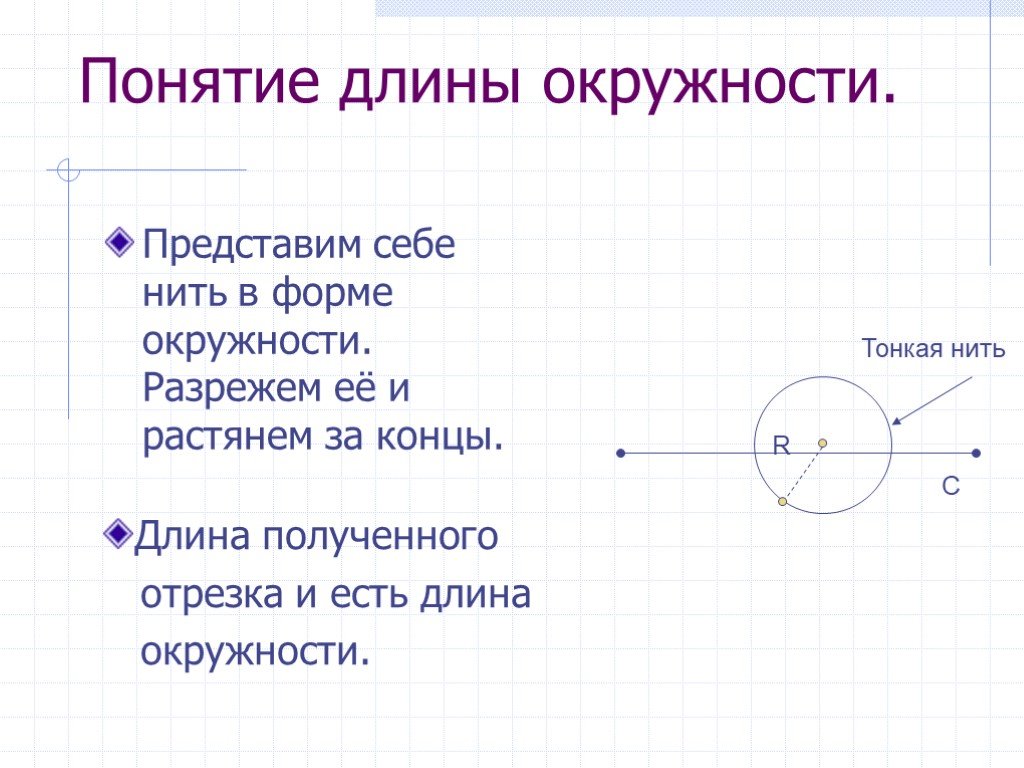
Представим. Что мы разрезаем окружность и «распрямляем» ее в нить. Длина получившегося в этом случае отрезка и есть длина окружности. Длина окружности ...Длина окружности и площадь круга
« Да, много решено загадок от прадеда и до отца, и нам с тобой продолжить надо тропу, которой нет конца…». (1. Обруч , 2. Радиус, 3. Кольцо, 4. Хорда). ...Длина окружности (5-6 класс)
Храм Покрова Пресвятой Богородицы, г.Озерск. Ротонда г.Озерск. Площадь им. Курчатова, г.Озерск. диаметр Окружность Колесо центр R D O радиус Окружность. ...Длина окружности и площадь круга
№ 840 № 855. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ. Решение 1 Sкольца = πr21 - πr22 = π(r21 – r22); π ≈ 3, r1 = 1,7 см, r2 = 1 см Sкольца = 3 (1,72 - 12)= 3 ...Длина окружности и площадь круга
О А С Д О - ОА - СД - центр радиус диаметр. π ≈ 3 4см С=2πr 24см 5дм 30дм 10м 60м 1м 6м r S. S=πr² 48см² 75дм² 300м² 3м². Известно, что во всех цирках ...Длина окружности и площадь круга
Назовите: а) окружность, б) круг. 1) 2) 4) 5) 6) 7). Дайте названия линиям и точкам Какой формулой связаны радиус и диаметр? ??? окружность центр ...Длина окружности. Площадь круга. Коллекция задач для 6 класса
. Великий древнегреческий математик Архимед (III в. до н.э.), выполнив множество измерений, установил, что длина окружности примерно в раза больше ...Площадь круга. Длина окружности
Тема : Площадь круга. Длина окружности. Цели и задачи: Закрепить основные понятия и определения по данной теме; проверить уровень сформированности ...Длина окружности. Площадь круга. Практические применения
Цели развивающие: Активизировать деятельность учащихся через разнообразные виды самостоятельной работы. Способствовать развитию долговременной памяти ...Масштаб. Длина окружности и площадь круга
Организационный момент. Устные упражнения. Работа по карточкам. Работа с самопроверкой. Задачи практического содержания. Самостоятельная дифференцированная ...Окружность. Длина окружности
Колесо Окружность Центр О R Радиус Диаметр. R - внутренней окружности. R1 - внешней окружности. ? Сначала было замечено, что длина любой окружности ...Длина окружности
Презентация урока раскрывает одну из важных тем математики 6 класса «Длина окружности». Презентация рассчитана на школьников 11-12 лет. Презентация ...Длина окружности и площадь круга
Цель: Проверить знания формул вычисления длины окружности и площади круга Пособие: круг с ниткой. Задания. 1.Найти длину окружности, практическим ...Длина дуги окружности
3π/4 В С D 0 Ι ΙІ ІІΙ ΙV L = 2πR R = 1, L = 2π ∙ 1 = 2π АС = π АВ = ВС = СD = DA = π/2 π 3π/2 А 5π/4 7π/4 π/4 ●. π/2 4π/3 2π/3 5π/6 7π/6 π/6 11π/6 ...Площадь круга и длина окружности
Повторение № 1 № 2 № 3 № 4 № 5 № 6 № 7 № 8. Задача. Веер имеет форму кругового сектора. Найдите площадь этого сектора и длину дуги, которую образует ...Окружающая среда и длина окружности
Dərsin məqsədi. 1. Çevrə və onun mərkəzi 2. Çevrənin radiusu,vətəri və diametri 3. Çevrənin diametri ilə radiusu arasındakı əlaqə 4. Çevrənin uzunluğu ...Конспекты
Длина окружности
МБОУ СОШ №38. Г.Иркутск. Дёмина Оксана. Олеговна. Учитель математики. Тема:. Длина окружности. Цели:. обучающая:. введение ...Длина окружности .Шар .Сфера
Учитель математики Вольф Лилия Арнольдовна КГУ « Горьковская СШ». Урок математики в 6 классе по теме: «Длина окружности .Шар .Сфера». Цели урока:. ...Длина окружности
Технологическая карта урока математика 6 класс. УМК «Сферы». . Дата: 5.02.15 ( урок № 97 ). Тема урока:. Длина окружности. Тип урока:. изучение ...Окружность. Длина окружности
Урок математики в 6 классе по теме. . «Окружность. Длина окружности». Цели:. Образовательная: формировать у учащихся понятие об окружности и ...Длина окружности
Тема урока: Длина окружности. Вид урока:. урок сообщения и усвоения новых знаний. Цели урока:. Обучающие. Опытным путем получить зависимость ...Длина окружности. Площадь круга. Шар
Урок № 33. Тема. :. Длина окружности. . Площадь круга. Шар. ЦЕЛЬ:. . Дидактическая. Учащиеся должны научиться:. - Вычислять длину окружности;. ...Длина окружности. Число Пи
Муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа №36 г. Томска. Конспект урока математики в 6 классе. ...Длина окружности. Площадь круга
Чичерова Татьяна Ивановна учитель математики МБОУ «Образцовская СОШ» Волгоградская обл. Тема урока:. . . Длина окружности. Площадь круга. 9 класс. ...Длина окружности. Площадь круга. Сфера. Шар
Тема: Длина окружности. Площадь круга. Сфера. Шар. Цели урока:. 1. Познакомить учащихся с практическими способами измерения длины окружности и ...Длина окружности, площадь круга, шар
Тема: «Длина окружности, площадь круга, шар», 6 класс. . Миннегалиева Раиля Хамитовна. учитель I квалификационной категории. МБОУ «СОШ №6» г.Нижнекамска ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 февраля 2019
Категория:Математика
Классы:
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию