Презентация "Что такое процент?" по математике – проект, доклад
Презентацию на тему "Что такое процент?" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 34 слайд(ов).
Слайды презентации
Список похожих презентаций
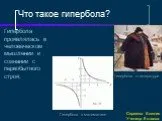
Что такое гипербола?
История происхождения гиперболы. Одним из первых, кто начал изучать конические сечения — эллипс, парабола, гипербола, был ученик знаменитого Платона, ..."Что такое подобные слагаемые?"
Что вы хотите получить сегодня на уроке? Повысить уровень знаний; Пообщаться с учителем; Пообщаться с товарищами; Посидеть и помолчать лишь бы не ...Что такое функция?
ЦЕЛЬ УРОКА дать представление о функции с помощью понятия «множество», показать связь между математикой и окружающим миром. Функцией в общем понимании ...Что такое дроби?
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Делимое называется числителем дроби, а делитель — знаменателем. ...Что такое числа?
КАКИМИ БЫЛИ ПЕРВЫЕ ЦИФРЫ? Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад. ...Что такое функция
Устный счет. При каких значениях переменной х имеет смысл выражение: 3х; 3-х; 3/х; x/3; 3/(x-3); (x+3)/3 Как расположена точка А на координатной плоскости ...Что такое понятие?
Как можно определить понятие? по признакам. С помощью чего строится видовое понятие? Классификация Тема. живая природа Животные Человек Растения. ...Что такое треугольник?
Что такое треугольник? В А С. Посмотрите на рисунок и ответьте на несколько вопросов: 1) Что изучает планиметрия? 2) Какая фигура изображена? 3) Из ...Что такое параллелограмм
Цели:. Ввести понятие параллелограмма. Рассмотреть свойства параллелограмма. Рассмотреть признаки параллелограмма. Решение базовых задач. ABCD – параллелограмм. ...Что такое пирамида ?
Термин “пирамида” заимствован из греческого “пирамис” или “пирамидос”. Греки в свою очередь позаимствовали это слово, как полагают, из египетского ...Что такое задача
Я, Корпатыч, Крош, Лосяш. Догоняем дружно мяч. Нюша с Ёжиком пока - Запасных два игрока. А когда подучатся, Сколько нас получится? 7 ромашек наша ...Что такое математика?
Слово «математика» произошло от др.-греч. máthēma, что означает изучение, знание, наука, и др.-греч. mathēmatikós, первоначально означающего восприимчивый, ...Что такое функция?
Цели урока:. Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины: зависимая переменная и независимая переменная (аргумент ...Что такое геометрия
Геометрия- одна из наиболее древних наук. Первые геометрические факты были найдены…. В Вавилонских клинописных таблицах и египетских папируса (III ...Что такое геометрия?
Подразделы геометрии:. Классическая геометрия. Классическая геометрия – геометрия точек, прямых и плоскостей, а также фигур на плоскости и тел в пространстве. ...Что такое геометрия
ПЛАН. Происхождение слова геометрия. 1. Что изучает геометрия. Причины возникновения геометрии. 3. Основоположники геометрии. 4. Слово геометрия древнегреческого ...что такое вероятность?
Цели и задачи урока. Цель: познакомить с понятием «вероятность». Задачи урока. Образовательная: научить решать задачи, совершенствовать умения и навыки ...Что такое функция
Цели урока:. Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины: зависимая переменная и независимая переменная (аргумент ...Что означают слова «с точностью до …»
Что означают слова «с точностью до …. Цель : ввести запись a ± h; способствовать усвоению терминологии; развивать навыки определения по записи промежутка, ...Что сначала? Что потом?
Что сначала? Что потом? Урок по математике в 1 классе УМК « Перспектива» авторы учебника Г.В. Дорофеев, Т.Н. Миракова. . Бабушка объяснила внуку, ...Конспекты
Что такое логика
Республика Коми. МОУ «Чимская основная общеобразовательная школа». Методическая разработка. внеклассного мероприятия. . по математике. ...Что такое математический язык
Математика 7 класс. Тема урока:"Что такое математический язык". Автор: учитель математике МАОУ "СОШ №108". Федоровцева Наталья Леонидовна. Познавательные ...Что такое функция?
Алгебра. . 7 класс. . «Что такое функция?». Цели:. Воспитать интерес к математике через использование нестандартных форм обучения;. . Ввести ...Что такое функция
МАРШРУТНЫЙ ЛИСТ обучения, взаимоконтроля и самоконтроля по теме:. Урок 1. . Тема. :. Что такое функция. . . ( учебник стр. 51-53). Класс 7 А. Фамилия, ...Что такое функция
Фрагмент урока с применением ИКТ по теме «Что такое функция», алгебра, 7 класс. Тип урока:. . Изучение нового материала. . Вид урока:. комбинированный ...Что такое модуль?
. Методический паспорт учебного проекта. . Название проекта. . Что такое модуль? . ФИО разработчика проекта. . . Веремеенко Светлана ...Что такое уравнение?
Тема:. Что такое уравнение? Цель: формирование понятия «уравнение», «корень уравнения», умения решать уравнения. Ход урока. 1.Мотивация. Прозвенел ...Что такое задача
Автор учебника:. И.И.Аргинская, Е.П.Бененсон, Л.С.Итина, С.Н.Кормишина. Тип урока:. . Урок «открытия» новых знаний. . Тема урока:. «Что такое ...Что такое линейка и что она умеет?
Тема: Что такое линейка и что она умеет? Цели:. Предметные. Познакомить учащихся с линейкой как чертёжным инструментом;. . Учить пользоваться ...Что такое дробь?
Урок математики 5 класс (программа и учебник Г.В. Дорофеева). Тема урока:. Что такое дробь? Первый урок по теме «Дроби» - 20 часов. Содержание ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 января 2019
Категория:Математика
Содержит:34 слайд(ов)
Поделись с друзьями:
Скачать презентацию