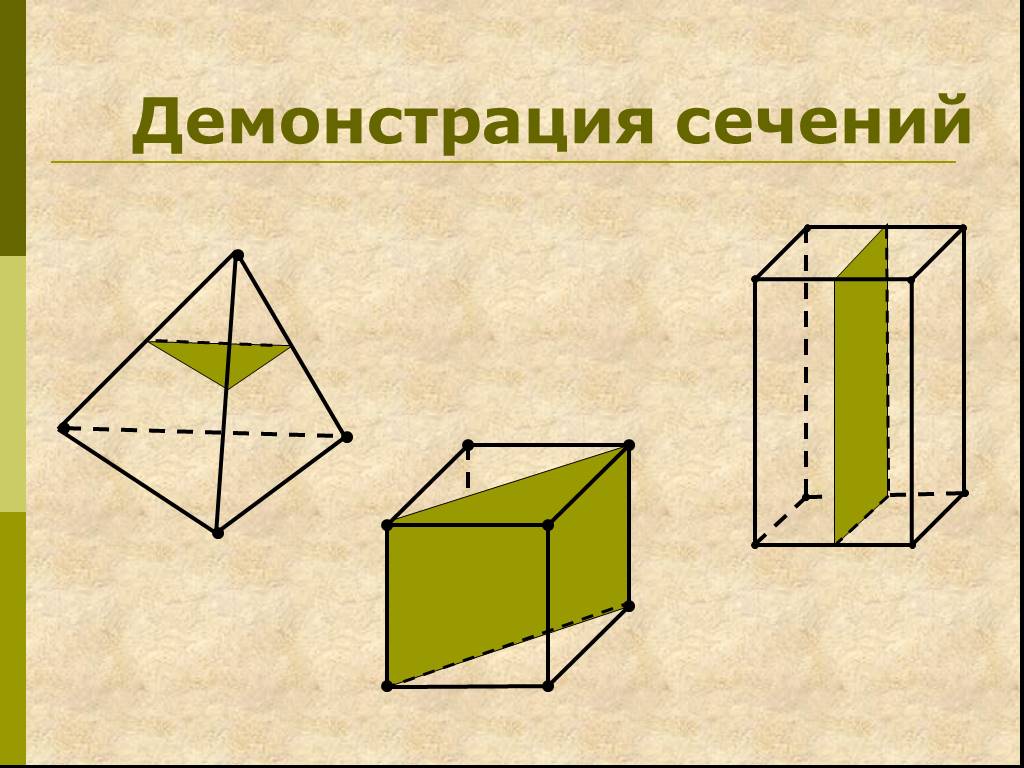
Презентация "Сечение многогранника плоскостью" по математике – проект, доклад
Презентацию на тему "Сечение многогранника плоскостью" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 32 слайд(ов).
Слайды презентации
Список похожих презентаций
Сфера, описанная вокруг многогранника
Определение: Многогранник называется вписанным в сферу (вписанным в шар), если все вершины многогранника принадлежат этой сфере. Про сферу в этом ...Угол между прямой и плоскостью
Перпендикулярны ли прямые а и в? Ответ обоснуйте. А В С D F b a. ABCD- прямоугольник, FB┴(ABC). ABCD- параллелограмм, FB┴(ABC). C B O ABCD- ромб, ...Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильного многогранника
Цель урока: Ознакомление с понятием симметрии в пространстве и с понятием правильного многогранника. Задачи урока: Ввести понятие правильного многогранника, ...Симметрия многогранника
Общие сведения о правильных многогранниках. По мнению многих, правильные многогранники, или как их еще называют Платоновы тела, обладают неповторимыми ...Сечение многогранников
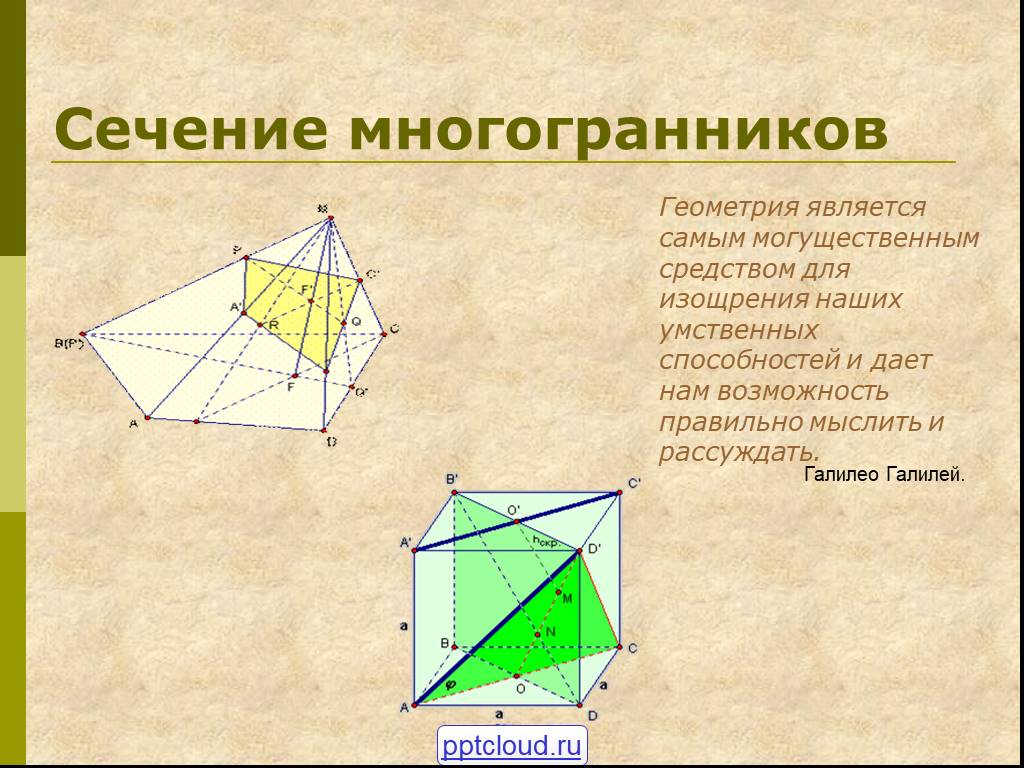
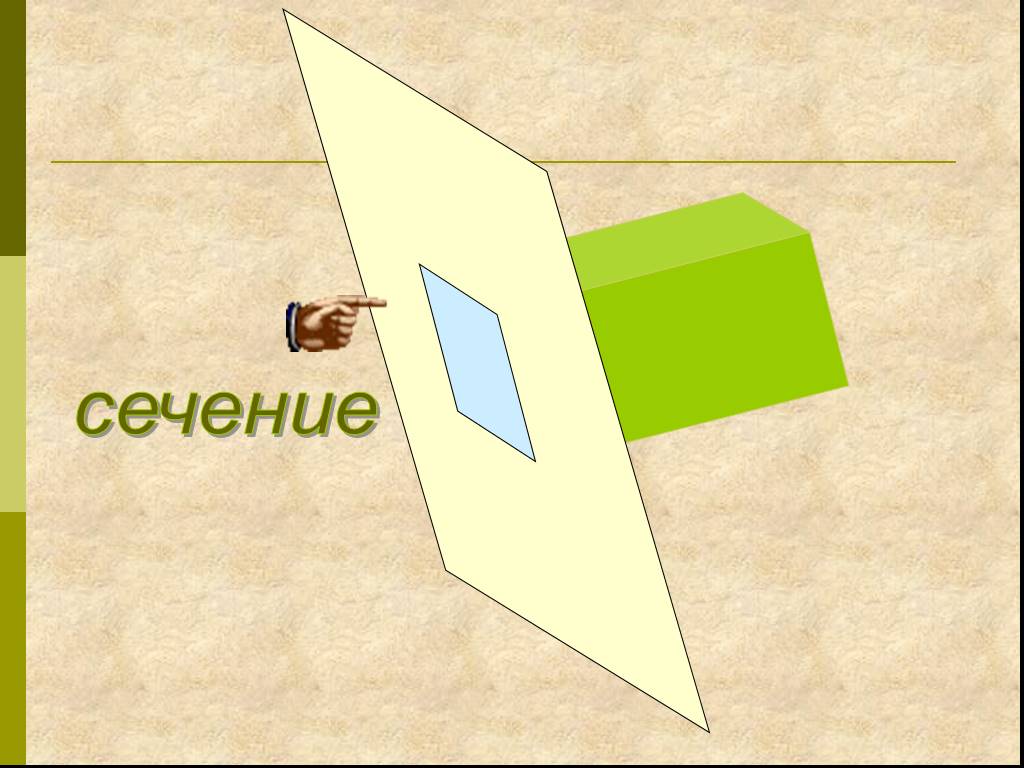
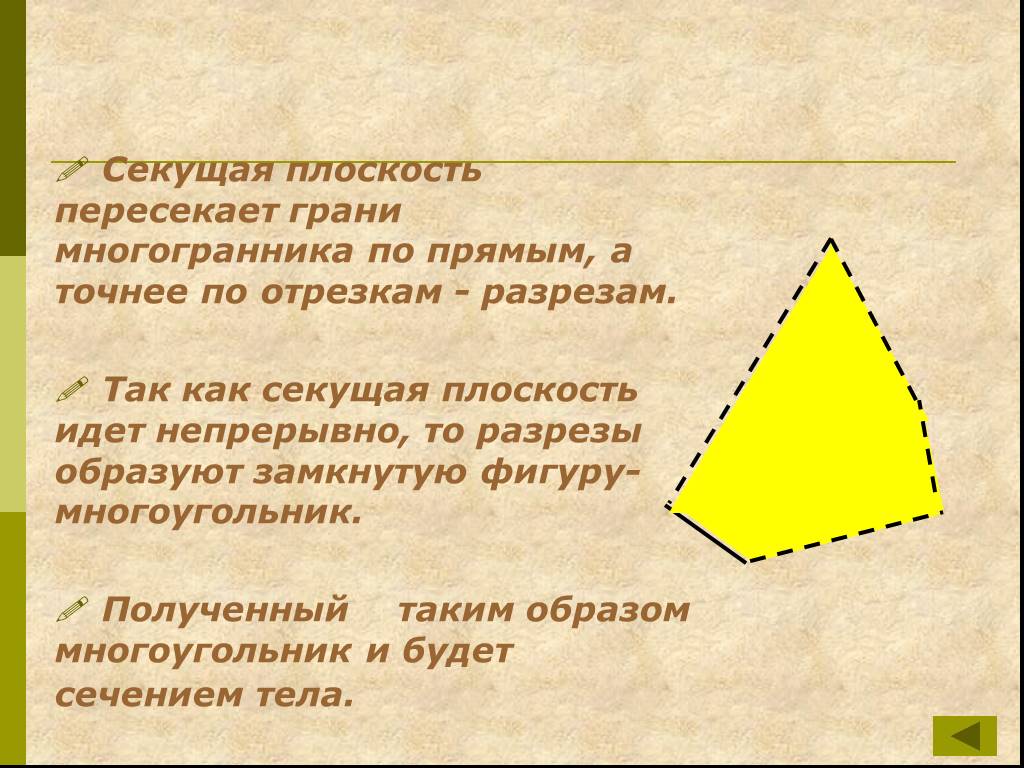
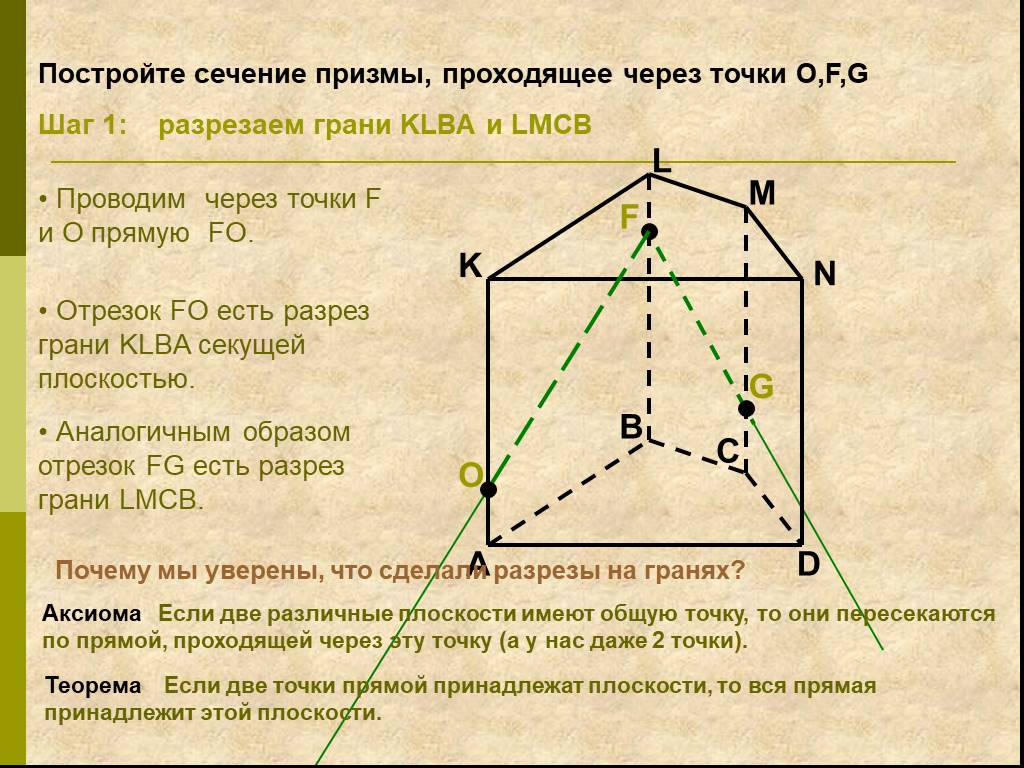
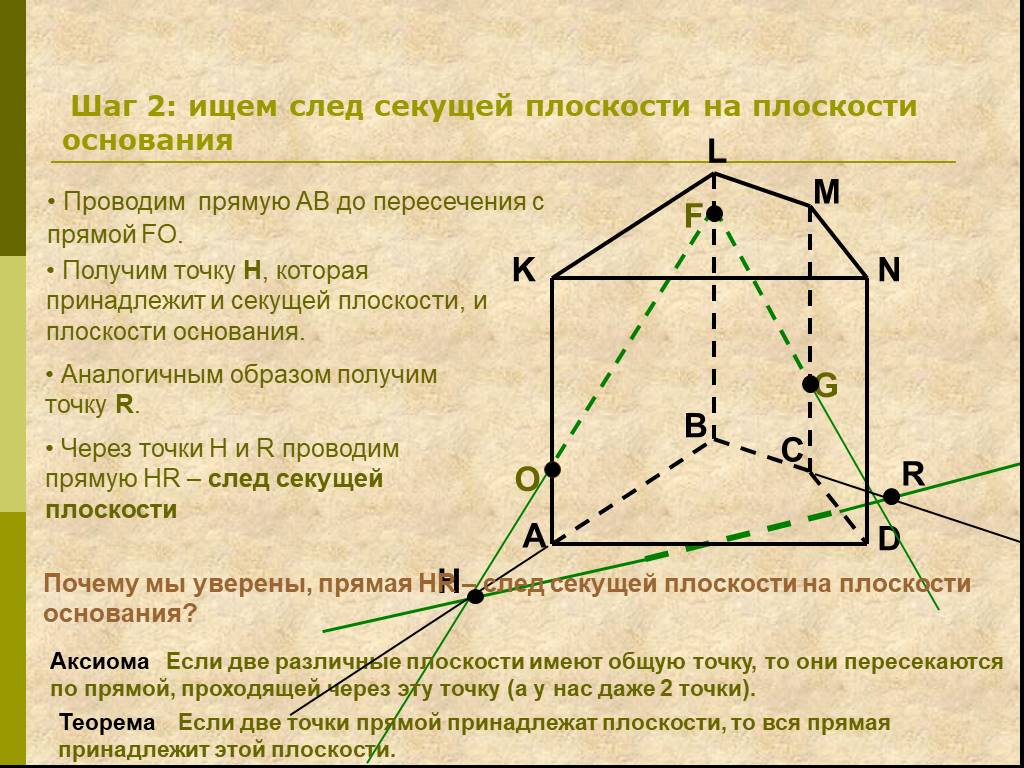
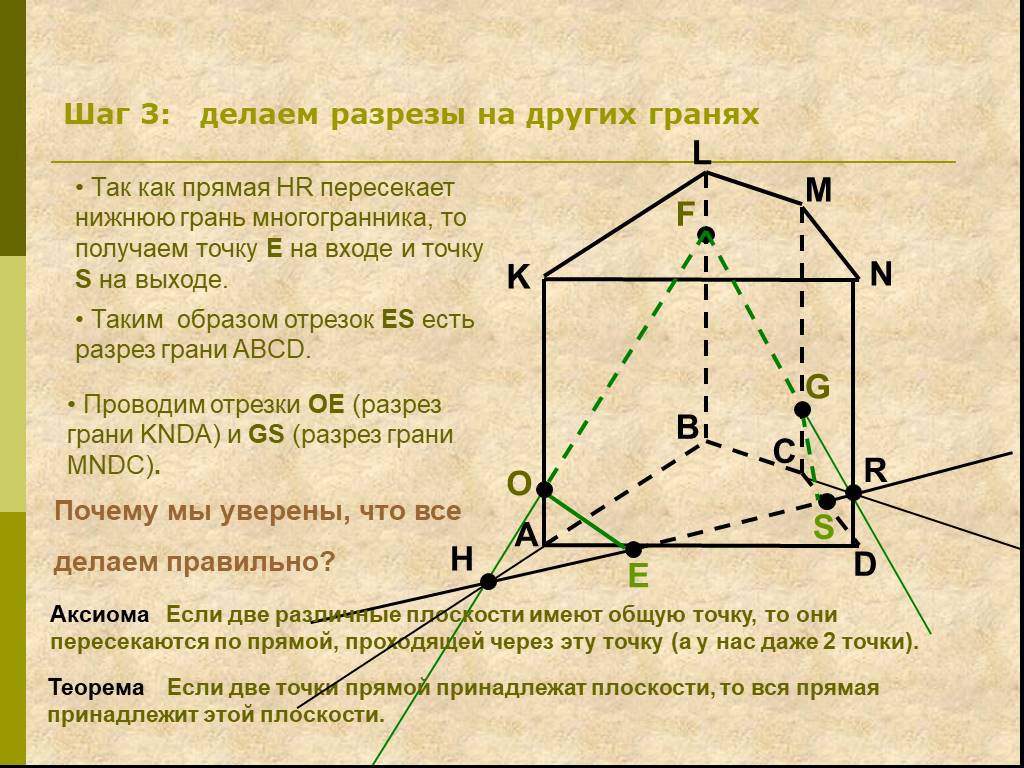
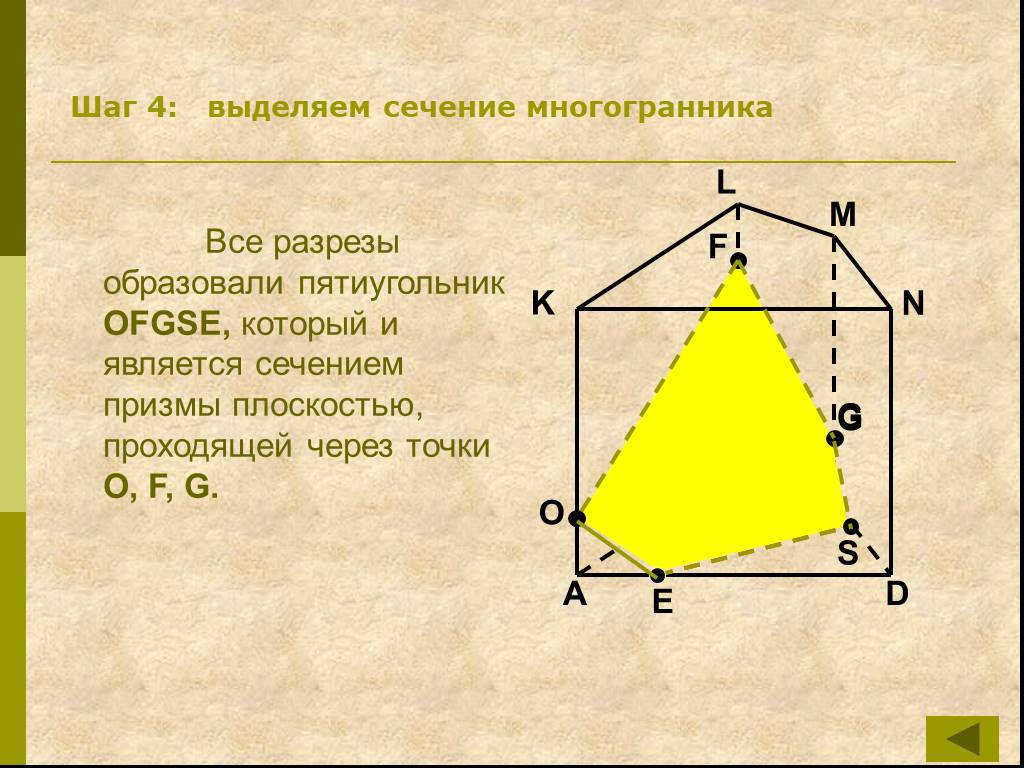
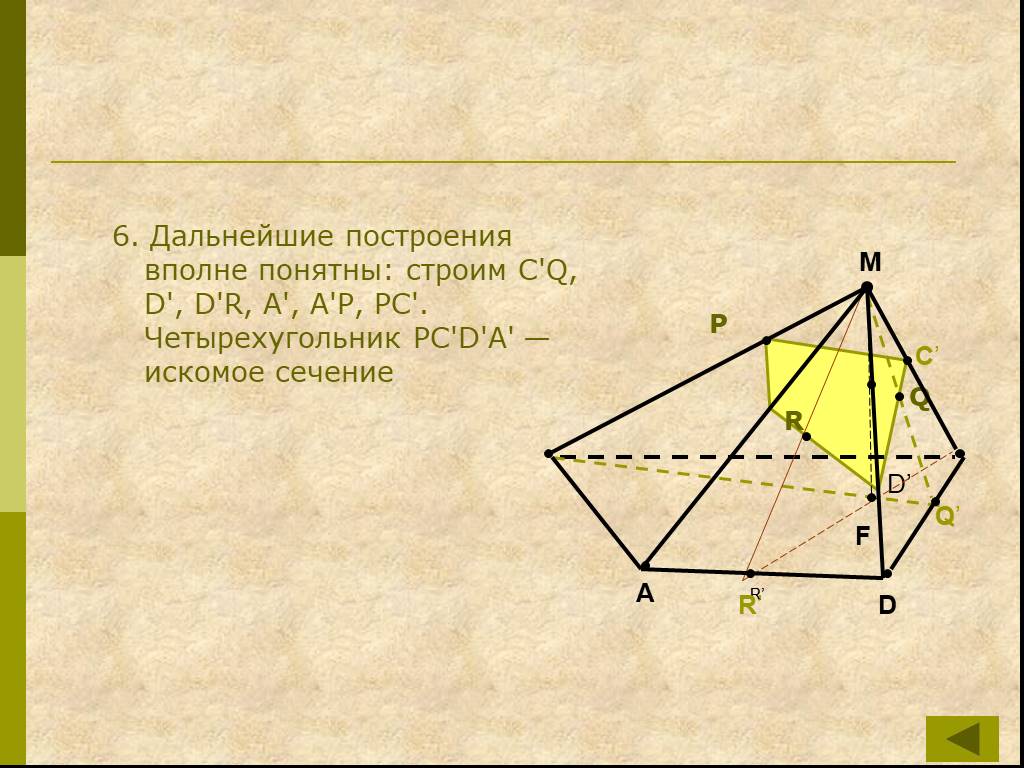
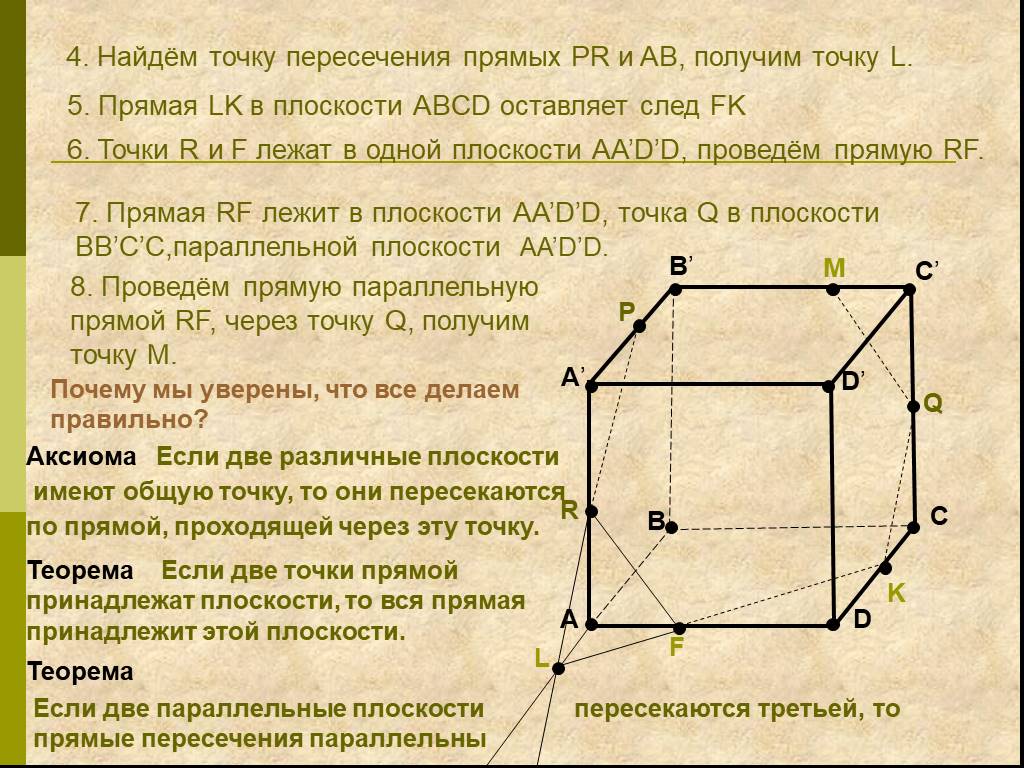
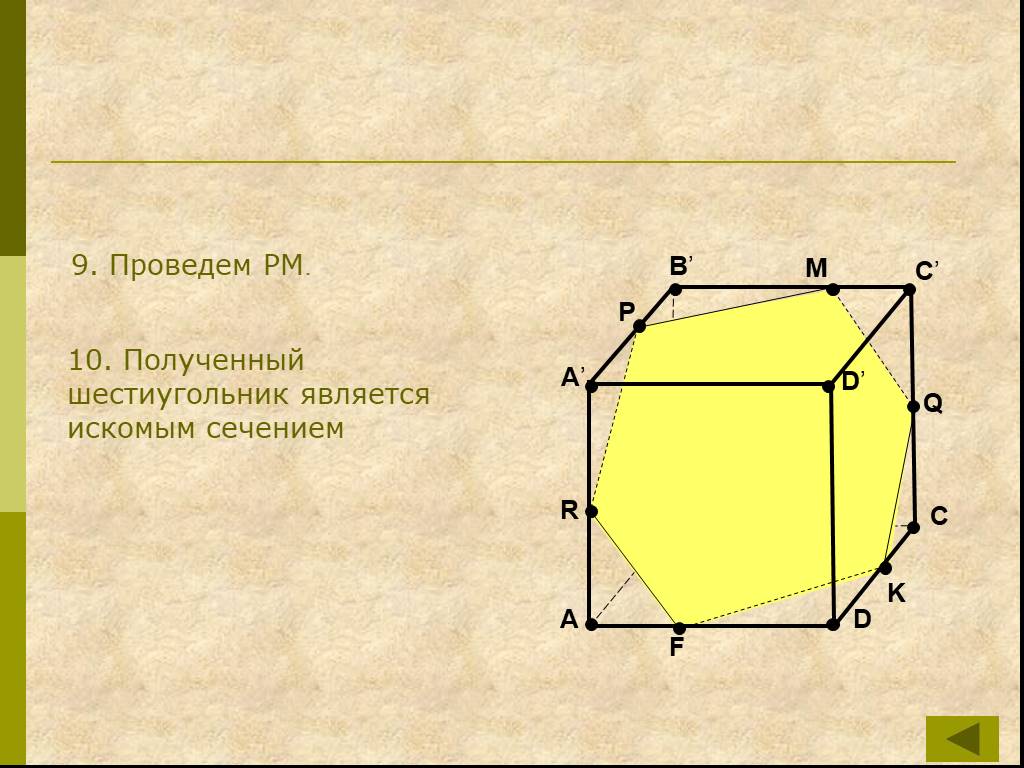
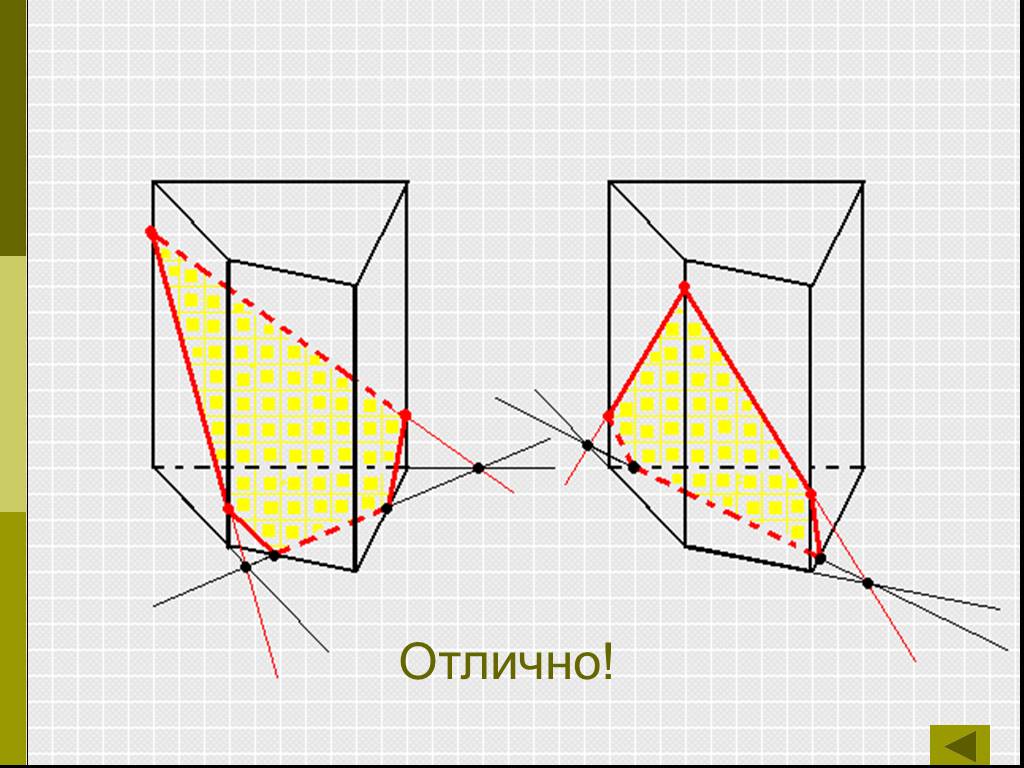
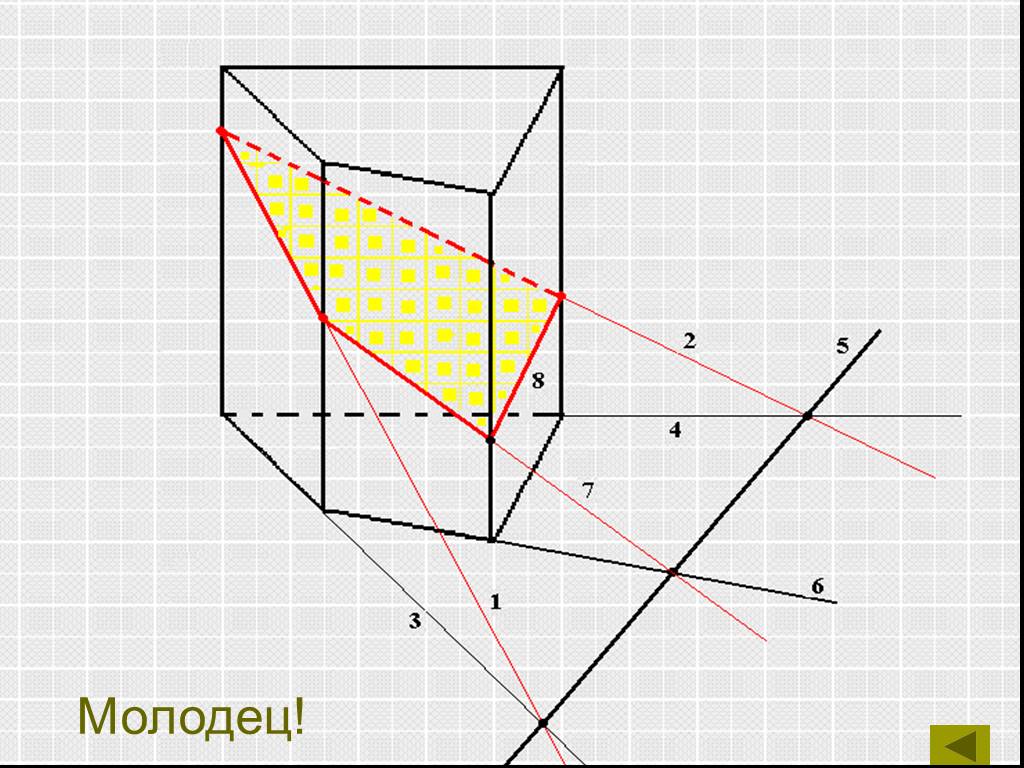
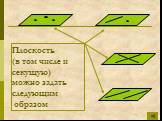
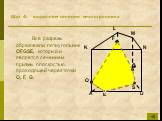
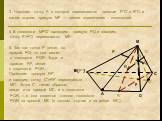
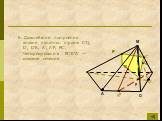
Определения:. Секущая плоскость - плоскость, по обе стороны от которой имеются точки данного многогранника. Многоугольник – сторонами которого являются ...Сечения многогранников плоскостью
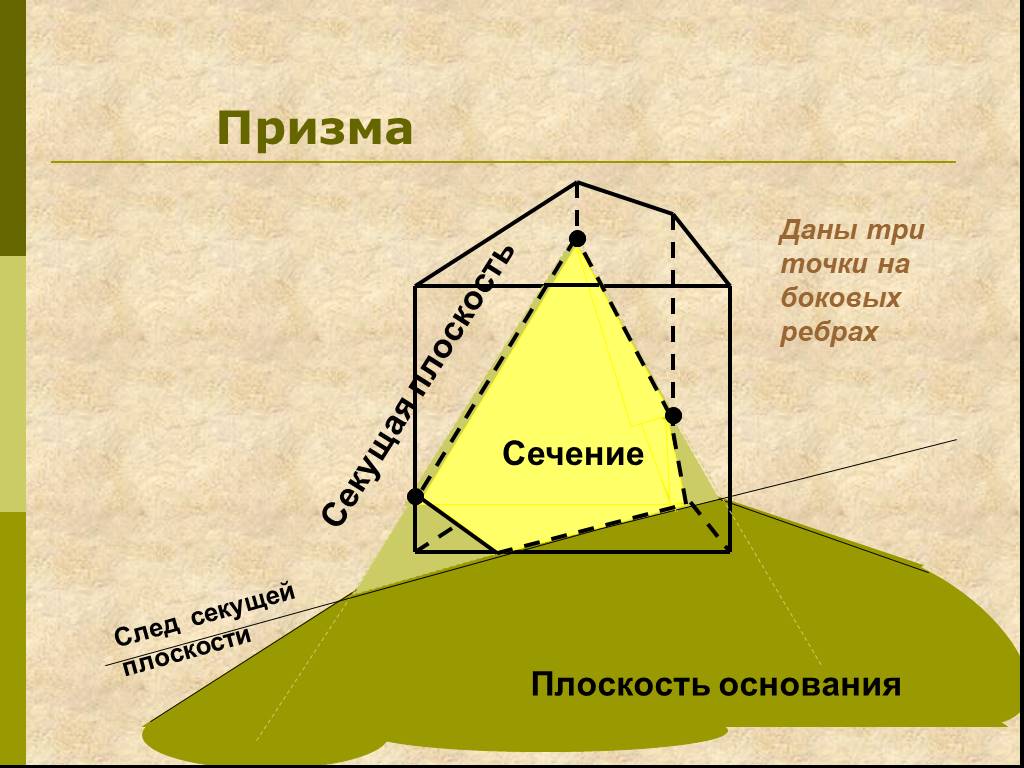
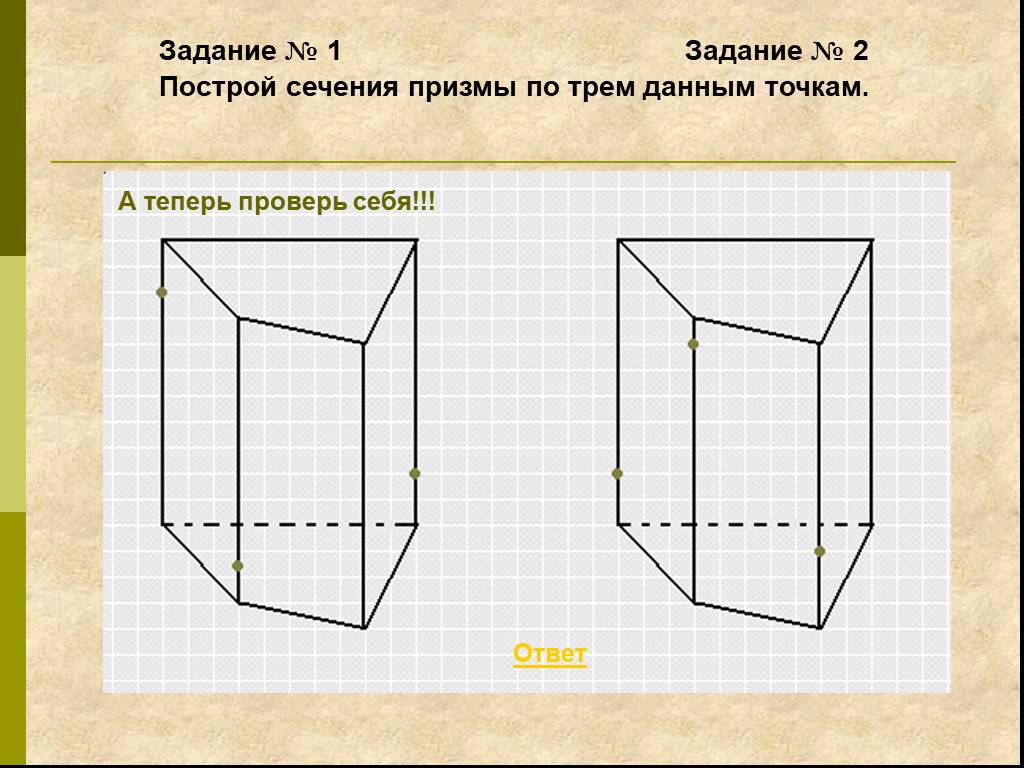
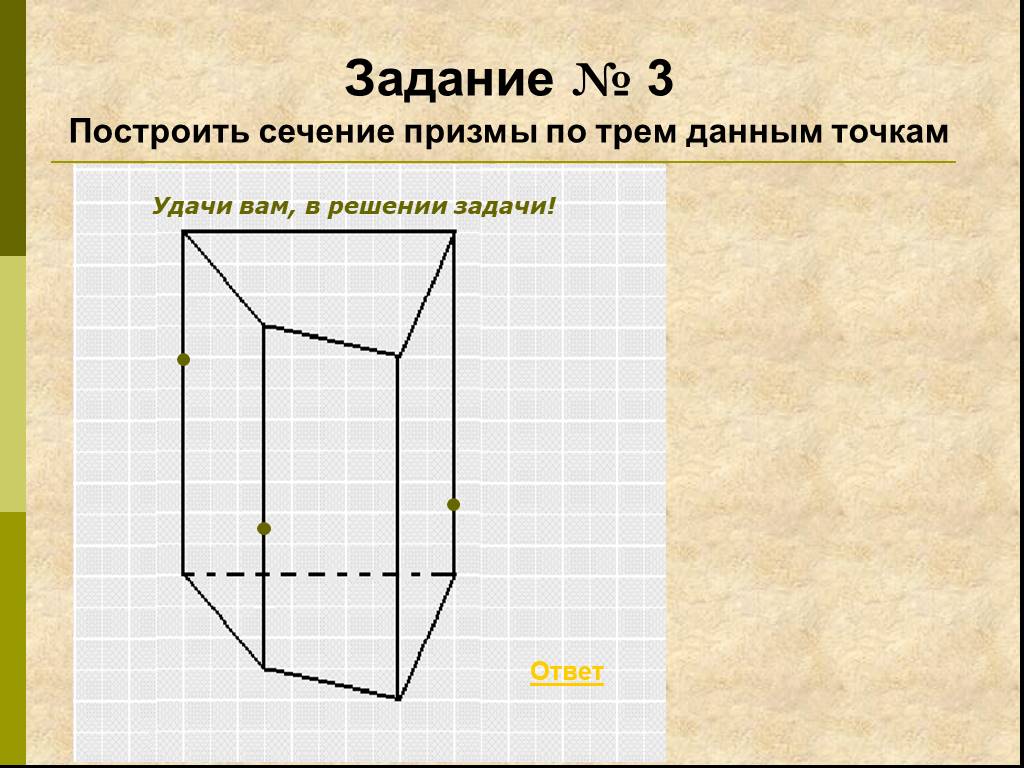
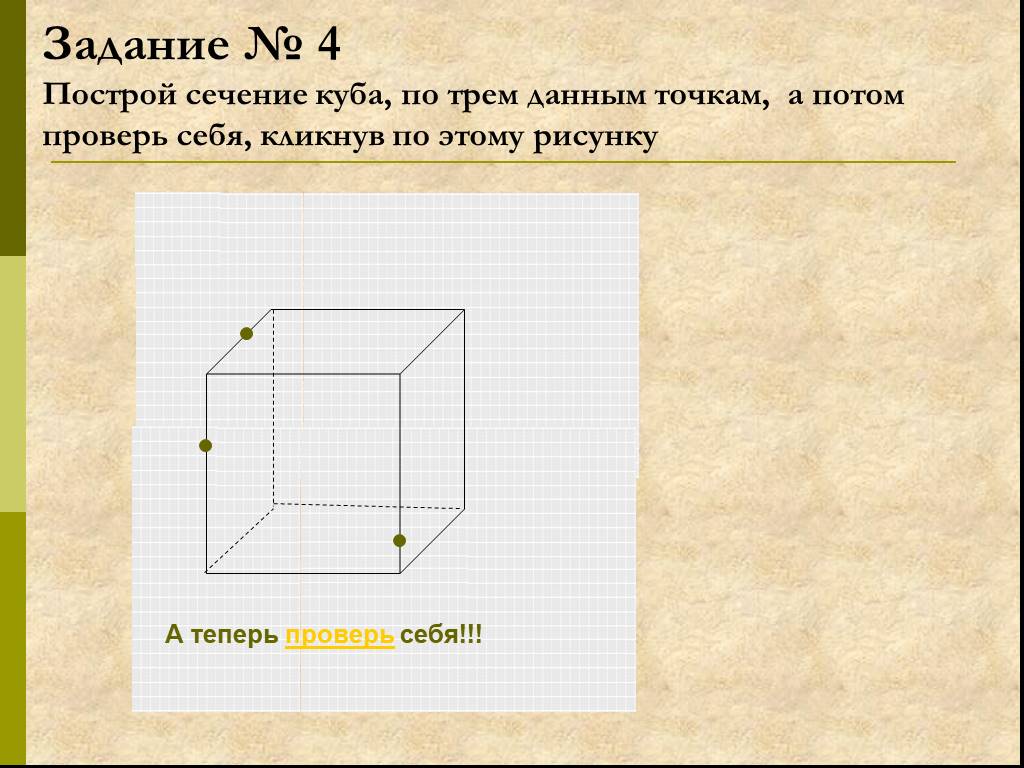
Работа с текстом задачи. Задача. Построить сечение пятиугольной призмы плоскостью, проходящей через три точки, одна из которых лежит в плоскости верхнего ...Сечение
Все знают: Сказку «Маленький принц». Ее написал отважный летчик и замечательный французский писатель ХХ века Антуан де Сент-Экзюпери (1900 – 1944). ...Цилиндр. Сечение цилиндра плоскостями
Как называется каждая фигура? Тема урока:. Цилиндр. Сечение цилиндра плоскостями. Цели урока:. ввести определение цилиндра и его элементов;. рассмотреть ...Понятие многогранника
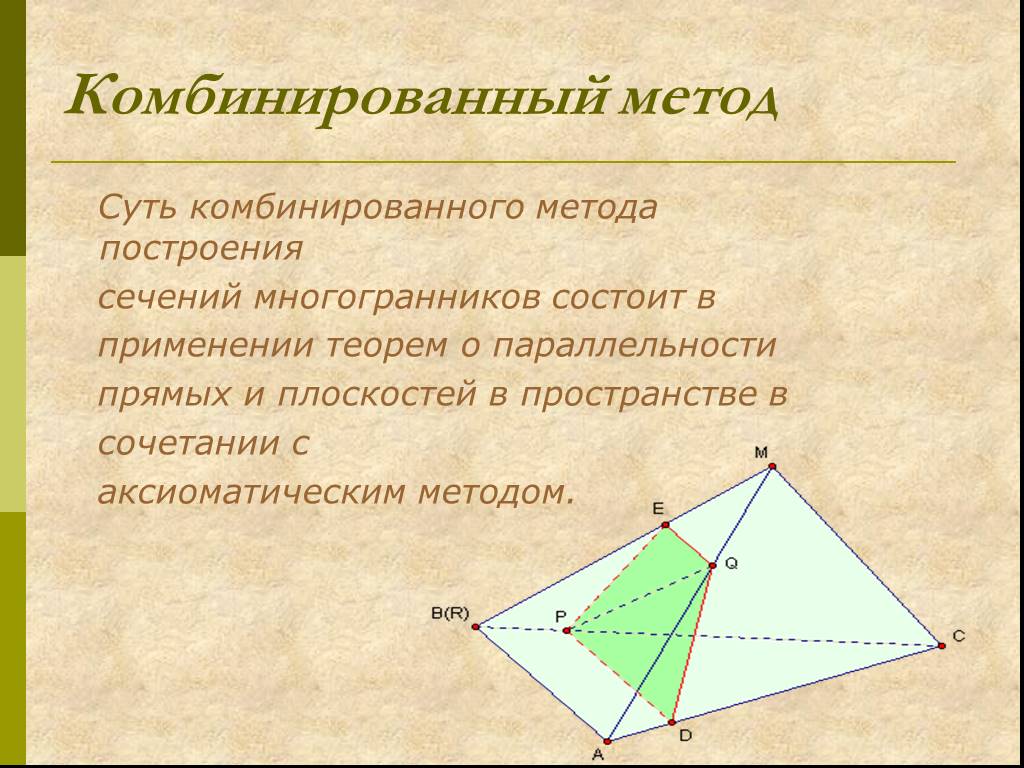
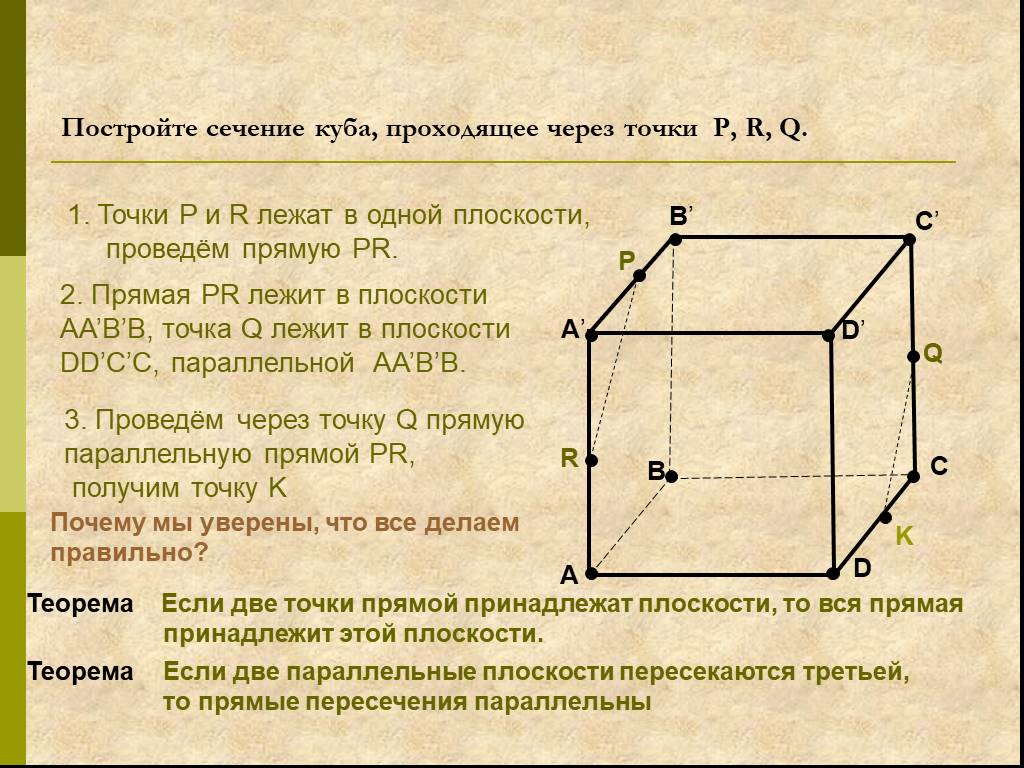
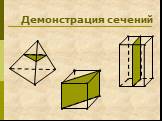
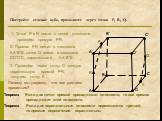
Многогранники Тела. Геометрические фигуры. Плоские Не многогранники. Определение многогранника. Многогранником называется ограниченное тело, поверхность ...Построение сечений многогранника
Содержание. Определение. Примеры построений сечений. Задания на построение сечений. Определение. Если пересечением многогранника и плоскости является ...Понятие многогранника
Что такое тетраэдр? Это геометрическое тело (поверхность), составленная из четырех треугольников. Что такое прямоугольный параллелепипед? Это геометрическое ...Понятие многогранника
1. Сумма углов треугольников равна…. 180 градусов. 2. Свойства углов равнобедренного треугольника при основании. В равнобедренном треугольнике углы ...Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку ...Угол между прямой и плоскостью
Теоретическая справка. Углом между наклонной и плоскостью называется угол между этой наклонной и ее проекцией на данную плоскость. Прямая, перпендикулярная ...Сечение
Сечение Тема урока:. ТЕМА: Сечение Цель урока:. Дать понятие о сечениях Дать понятия о видах сечений (наложенные, вынесенные) Научить учащихся определять ...Угол между прямыми. Угол между прямой и плоскостью
Две пересекающиеся прямые в пространстве определяют единственную плоскость, поэтому угол между пересекающимися прямыми в пространстве определяется ...Объём многогранника
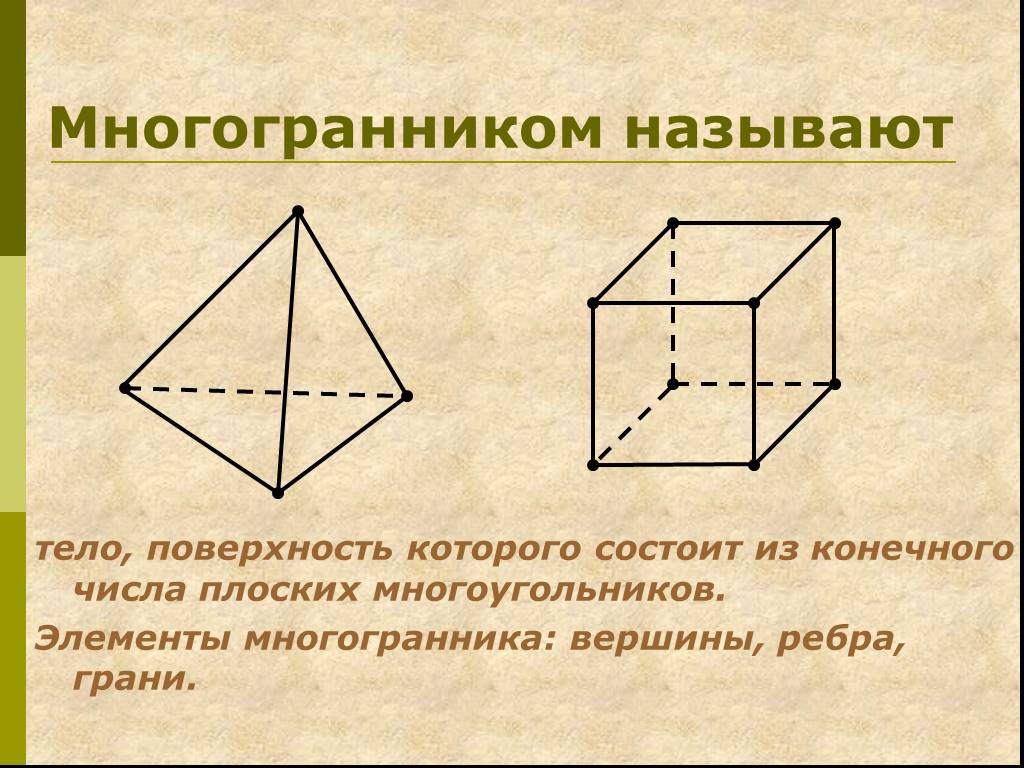
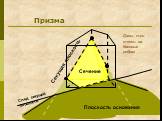
Многогранник. Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Многогранник называется выпуклым, ...Конус. Сечение конуса плоскостями
Конусом называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, ...Страна геометрия
Правительство. Отдел планирования. Отдел проектирования. Район археологических раскопок. Юбилей Первые поселения. Силурийский период. Средневековье ...Простая геометрия в архитектуре различных эпох и культур
Архитектура. Уже в XII в. архитектура понимается уже как наука, как знание, как геометрия, имеющая практическое приложение, как деятельность, требующая ...Конспекты
Построение сечений многогранника
Матлашевская Лилия Петровна. Учитель математики. . МАОУ «Гимназия № 2» г.Перми. Построение сечений многогранника. Цели и задачи урока:. Закрепление ...Многогранник. Элементы многогранника - грани, вершины, ребра
Технологическая карта урока. Математика, 4 класс «Б», учитель Сидорова О.А. Тема:. Многогранник. Элементы многогранника - грани, вершины, ребра. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 декабря 2018
Категория:Математика
Содержит:32 слайд(ов)
Поделись с друзьями:
Скачать презентацию