Презентация "Окружность" по математике – проект, доклад
Презентацию на тему "Окружность" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 29 слайд(ов).
Слайды презентации
Список похожих презентаций
Окружность и круг: теория и практика
Цель уроков: ввести понятия окружности и круга, разобрать связанные с ними понятия и формулы , отработать это на задачах и проверить степень усвоения ...Окружность круг
Тема: Окружность и круг. 22.12.2011. КРУГ ОКРУЖНОСТЬ. О. Точка О – центр окружности. А. ОВ, ОА, ОС- радиусы АС- диаметр. радиус С В ДИАМЕТР. D E F ...Окружность и круг
Н Ь С Т. 6.Сколько кубических сантиметров в одном кубическом метре? 7.Как найти объем прямоугольного параллелепипеда? 8.Чему равен объем куба, длина ...Окружность и круг урок
Содержание. Введение Основные понятия, связанные с окружностью и кругом Основные теоремы и свойства, связанные с окружностью и кругом Основные формулы, ...Окружность и круг
Какие виды линий изображены на рисунке? . КРУГ ОКРУЖНОСТЬ. Циркуль мой, циркач лихой, Чертит круг одной ногой, А другой проткнул бумагу, Уцепился ...Окружность и круг
У круга есть одна подруга, Знакома всем ее наружность, Она идет по краю круга, И называется окружность. О. Окружность и круг. Урок математики в 5 ...Окружность ее центр и радиус
Устный счет. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Назовите четвертую фигуру, не нарушая закономерности. ...Окружность, ее центр и радиус
Устный счет. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Назовите четвертую фигуру, не нарушая закономерности. ...Окружность
По какому признаку равны треугольники ? А В N С D. По двум сторонам и углу между ними. А В С D O. По стороне и двум прилежащим к ней углам. По трём ...Окружность в аксонометрии
Фронтальная диметрическая проекция. Z X Y V H W НЕТ. Изометрическая проекция. y. Построение овала в горизонтальной плоскости проекции. окружность ...Окружность
Что это? Область. Географическое понятие. Математическое понятие. Область-. часть страны (из словаря Ожегова). часть плоскости, ограниченная линией. ...Окружность
Цели урока: ввести понятие определения; систематизировать сведения об окружности, известные учащимся из курса математики предыдущих классов; уделить ...Окружность
Теорема. В любой треугольник можно вписать окружность. Доказательство: Рассмотрим АВС. Проведем биссектрисы треугольника, пересекающиеся в точке ...Окружность круг сфера шар
диаметр Окружность Колесо центр R D O радиус 3,14159265359 p ». Окружность. Длина окружности. C = pD C = 2pR. ПЛОЩАДЬ КРУГА ·(a · n) · h Sмн-ка= ·(a ...Окружность и круг
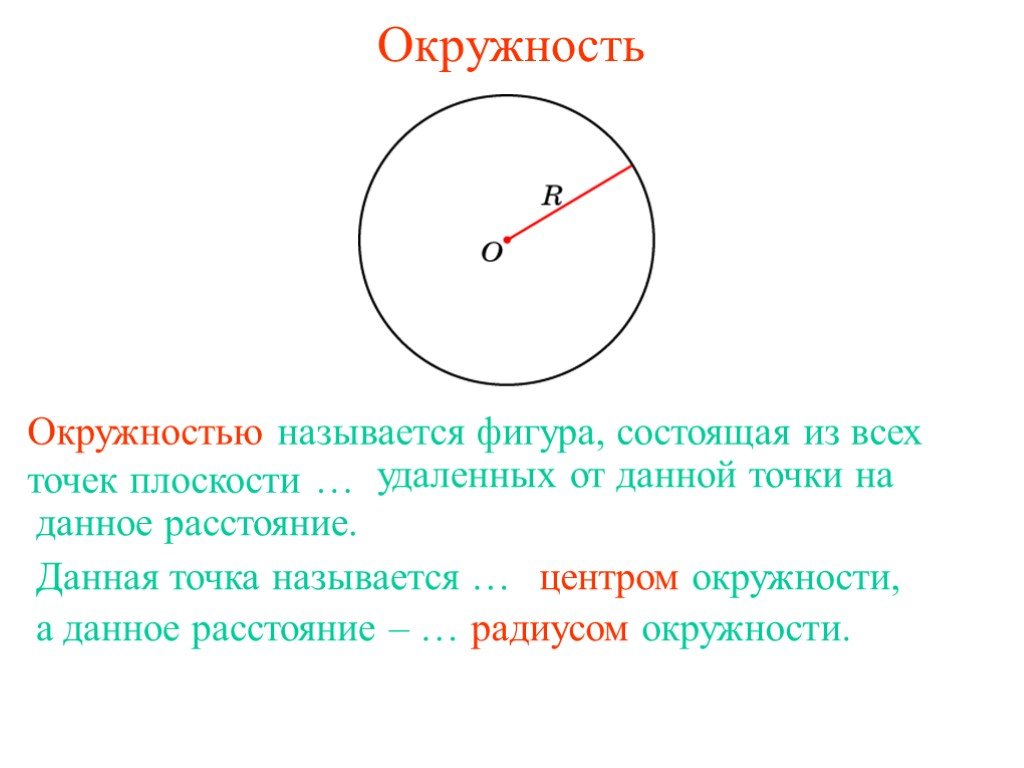
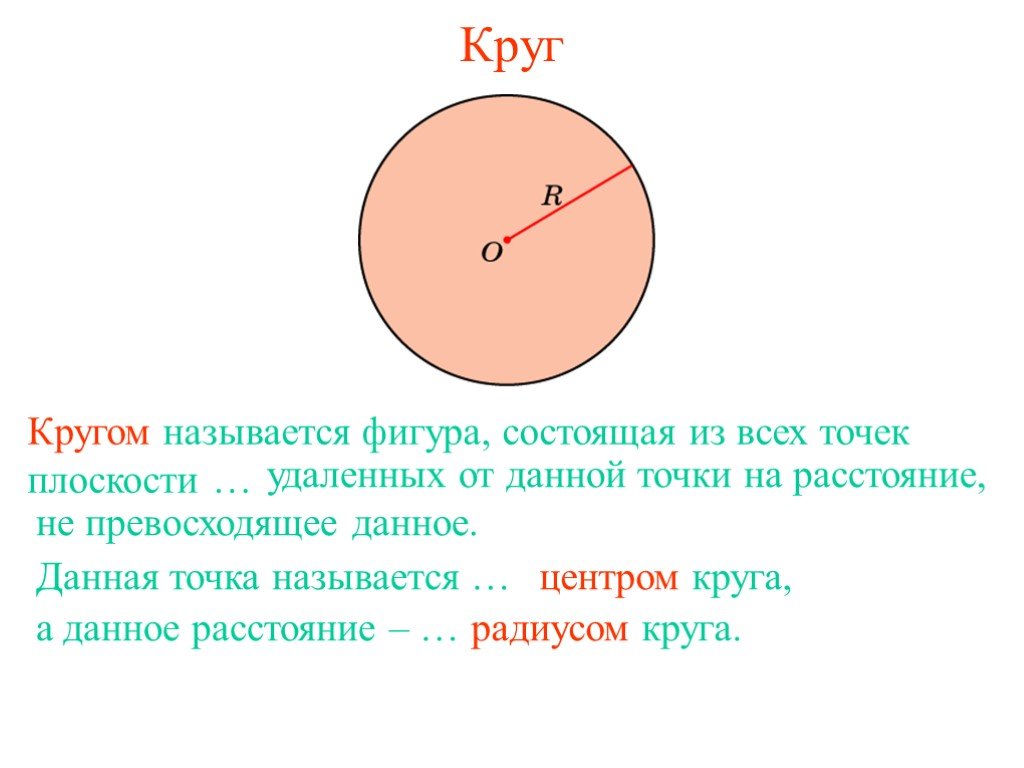
Определение. Окружность - геометрическая фигура, состоящая из всех точек, расположенных на одинаковом расстоянии от заданной точки (центра). Круг ...Окружность, длина окружности
диаметр Окружность центр R D O радиус. Окружность. Длина окружности. А В С D = 2R R = D : 2. Заполните таблицу:. 2,7 5,6 18 11 1 5 8 1 2 5,4 2,8 9 ...Окружность
Чем больше я знаю, Тем больше умею. У круга есть одна подруга, Знакома всем её наружность. Она идёт по краю круга И называется……. ОКРУЖНОСТЬ. Рисунок ...Итоговое повторение по темам "Окружность", "Многоугольники"
8 9 10 11 14 15 16 17 18 30 1 3 4 5 6 13 19 7. Дано: К А М О С N В Найти:. 2. ? C B. D. E 24. P K M. . 1260 A O. . . R1 R2. 1200. 12. 1500. . O2 O1. ...Страна геометрия
Правительство. Отдел планирования. Отдел проектирования. Район археологических раскопок. Юбилей Первые поселения. Силурийский период. Средневековье ...Простая геометрия в архитектуре различных эпох и культур
Архитектура. Уже в XII в. архитектура понимается уже как наука, как знание, как геометрия, имеющая практическое приложение, как деятельность, требующая ...Конспекты
Окружность, её центр и радиус
Проект урока математики. Наталья Михайловна Моисеенко,. учитель начальных классов. Муниципальное бюджетное общеобразовательное учреждение «Средняя ...Окружность, круг
Конспекта урока по математике по теме: « Окружность, круг». Терентьева Наталья Александровна, учитель начальных классов. Цели и задачи урока. :. ...Окружность и круг
Кузьмина Людмила Николаевна – учитель математики МБОУ «Туора-Кюельская СОШ с углубленным изучением отдельных предметов им.П.П.Кочнева». Предмет:. ...Окружность и круг
Тема урока «Окружность и круг». Цели урока. :. 1. Образовательная: формировать у учащихся понятие об окружности и круге, как о. . геометрических ...Окружность и круг
План-конспект урока по учебнику «Математика. 5 класс». . . Авторы: Виленкин. Тема:. «Окружность и круг». Тема. Окружность и круг. . ...Окружность и круг
Урок математики в 5 классе по теме «Окружность и круг». Технологическая карта урока. Учитель. Сергеева Надежда Ильинична, учитель математики ...Окружность
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №66 г.Пензы. Урок по математике на тему: «Окружность». ...Окружность
ПЛАН-КОНСПЕКТ УРОКА Касательная к окружности. (Тема урока). . . ФИО (полностью). . Идрисова Раиля Гайзулловна. . . . . ...Окружность
Конспект урока. . Учитель:. . Доброумова Ольга Викторовна. Класс:. 7. Предмет:. геометрия. Тема:. . Окружность. УМК. :. Л.С.Атанасян и др. ...Окружность
Муниципальное БЮДЖЕТНОЕ образовательное учреждение. средняя общеобразовательная школа №14 «Зелёный ШУМ». города волжского волгоградской области. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:8 января 2019
Категория:Математика
Содержит:29 слайд(ов)
Поделись с друзьями:
Скачать презентацию