Презентация "Моделирование сюжетных задач" по информатике – проект, доклад
Презентацию на тему "Моделирование сюжетных задач" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 52 слайд(ов).
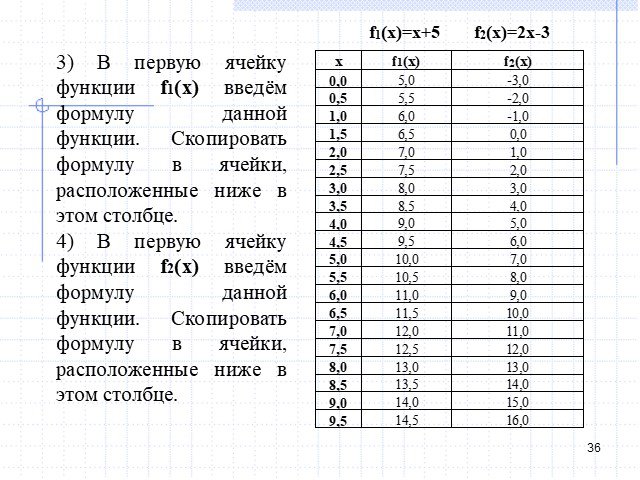
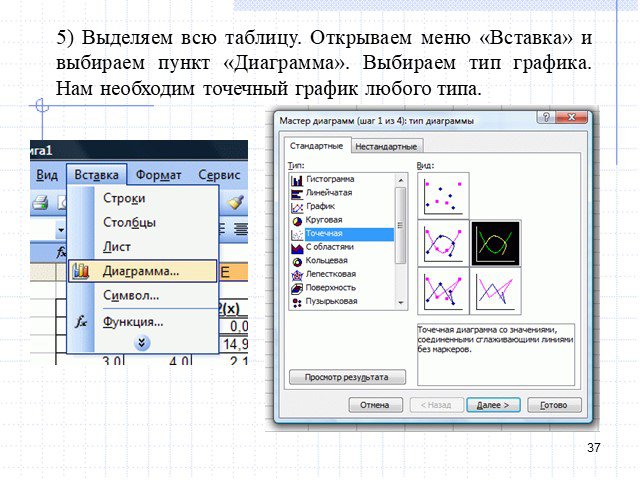
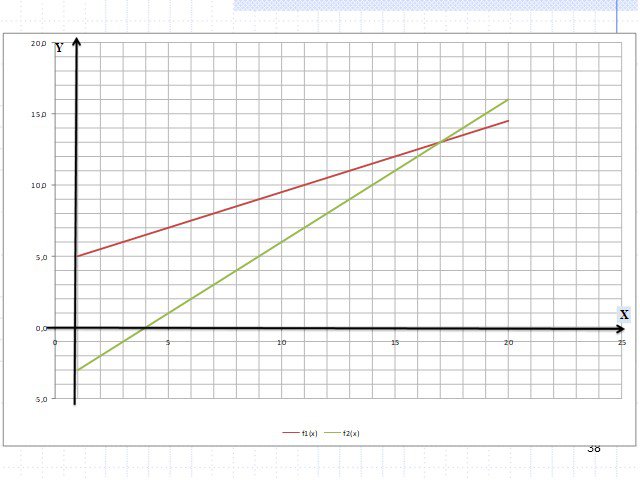
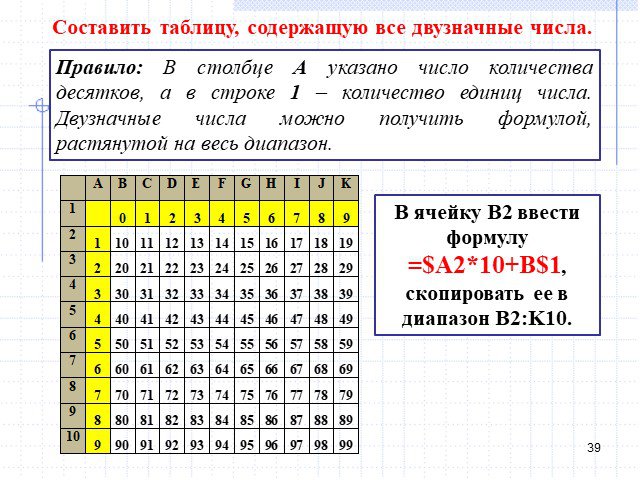
Слайды презентации
Список похожих презентаций
Математическое моделирование. Численные методы и использование ЭВМ в решении прикладных задач
Процесс мат. моделирования. Систематизация. Реальная ситуация. Сбор данных. Постановка задачи. Физическая модель. Декомпозиция. Математическая модель. ...Моделирование. Решение популяционных задач
Популяция и популяционная динамика. В биологии: популяция - совокупность особей вида, входящая в состав биогеоценоза. Популяционная динамика, - исследует ...Решение текстовых логических задач
Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распростра-нение получили следующие три способа решения ...Решение логических задач с помощью таблиц
РТ задача № 127 стр.111. Ответ: Лена любит блины с вареньем, Аня – пироги с вареньем, Ваня- пироги с капустой и Света любит оладьи со сметаной. РТ ...Решение логических задач
Проверка домашней работы:. § 1.3.4 РТ. № 84(б) № 88 (а). Кутепова Н.В, МОАУ «СОШ №4 г.Соль- Илецка Оренбургской обл.»2016 г. По 1 баллу. Что такое ...Решение задач с помощью графов
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице: Определите ...Решение задач на тему: «Определение количества информации»
Содержательный подход к измерению информации. Пример 1. При приеме некоторого сообщения получили 7 бит информации. Сколько вариантов исхода было до ...Решение задач линейного программирования в MS Excel
Общая задача линейного программирования решается симплексным методом Симплекс (лат. simplex - простой) – простейший выпуклый многогранник в n-мерном ...Построение семантических моделей для решения задач
Определение. Семантическая модель - это модель знаний в форме графа, в основе которой лежит идея о том, что любые знания можно представить в виде ...Моделирование
Моделирование – это деятельность человека по созданию моделей. Модели. Модель – это упрощенное подобие реального объекта, отражающее существенные ...Моделирование
это … атома. это … самолета. Это - … Земли. Это – фото…. МОДЕЛЬ. Моделирование как метод познания. Автор: Данилова Ю.А. учитель информатики МОУ СОШ ...Моделирование
Модель - это такой материальный или мысленно представляемый объект, который в процессе изучения замещает объект-оригинал, сохраняя некоторые важные ...Моделирование
Модель. Модель- это объект- заменитель, который в определенных условиях может заменять объект- оригинал. Модель воспроизводит некоторые интересующие ...Моделирование
Разгадайте ребус. В своей деятельности человек очень часто использует модели, то есть создает образ того объекта, явления или процесса, с которым ...Знаковые модели. Моделирование и формализация
Ключевые слова. словесные модели математические модели компьютерные модели. Словесные модели. Словесные модели - это описания предметов, явлений, ...Этапы решения задач на компьютере
Определение. Алгоритм – это предписание исполнителю выполнить последовательность команд, приводящую от исходных данных к искомому результату. Повторение. ...Паскаль. Циклы. Решение задач с помощью циклов
ЦИКЛЫ. В Паскале три вида циклов: Цикл For (со счетчиком); Цикл While (с предусловием); Цикл Repeat (с постусловием). Цикл FOR. For позволяет выполнить ...Моделирование бизнес-процессов с помощью ALLFusion Process Modeler
Фазы разработки Информационных Систем. Анализ. Определение, как работает система (будет работать) Планирование. Описание подсистем и их интерфейса ...Реализация воспитательных задач урока в процессе познавательной деятельности учащихся
Главной целью урока является развитие каждой личности, в процессе обучения и воспитания. Реализация воспитательных целей, воспитательных требований ...Моделирование в среде графического редактора PAINT
МОДЕЛИРОВАНИЕ В СРЕДЕ ГРАФИЧЕСКОГО РЕДАКТОРА. Модель – это аналог (заместитель) оригинала, отражающий некоторые его характеристики. Моделирование ...Конспекты
Этапы решения задач
. Информатика 9 «В» -29.09.2014 Проверила. . 9 «А»- 30.09.2014 заместитель директора. 9 «Б»-1.10.2014 по УВР Купенова К.К. ________29.09.2014. ...Разнообразие задач обработки информации
Урок 22. Разнообразие задач обработки информации. Планируемые образовательные результаты:. . предметные. – представление об информационных задачах ...Решение транспортных задач на уроках информатики (пример решения задачи)
Автор: Нестеренко Олеся Викторовна. Место работы: г. Калининград МАОУ СОШ №45. Должность: учитель математики и информатики. Тема: Решение ...Табличное решение логических задач
. Тема «Табличное решение логических задач». 7 класс (второй урок). Цели урока:. систематизировать и обобщить сведения, полученные учащимися ...Решение задач с помощью электронных таблиц
Решение задач с помощью электронных. . По звонку учащиеся заходят в класс. В это время первый слайд презентации на экране, учитель объявляет тему ...Решение логических задач
Конспект урока по информатике и ИКТ. Тема: Представление информации в табличной форме. «Решение логических задач». 5 класс. ...Моделирование в электронных таблицах
Конспект урока по информатике в 11 классе. «Моделирование в электронных таблицах». Цель урока:. развитие умений и навыков учащихся при создании ...Решение задач оптимизации в MS Excel
Нестеренко Олеся Викторовна. Учитель математики и информатики. МАОУ СОШ №45 г. Калининграда. Решение задач оптимизации в MS. Excel. . . ...Моделирование в графическом редакторе Paint. Всё, что мы видим, имеет конструкцию
Интегрированный урок информатики и труда по теме: "Моделирование в графическом редакторе Paint. Всё, что мы видим, имеет конструкцию". Симонова Татьяна ...Моделирование в электронных таблицах
муниципальное бюджетное общеобразовательное учреждение. Ремонтненская гимназия №1. Открытый урок. Зёрна разума. Моделирование в электронных ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Информатика
Автор презентации:учитель информатики Нигматуллин Радий Радиевич
Содержит:52 слайд(ов)
Поделись с друзьями:
Скачать презентацию






















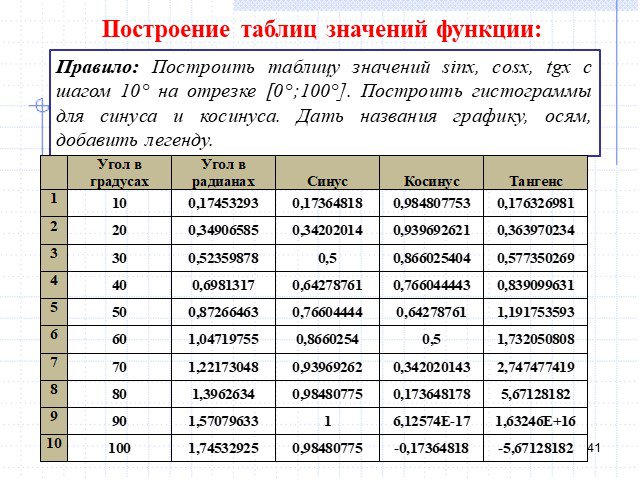




































![Построение таблиц значений функции: Правило: Построить таблицу значений sinx, cosx, tgx c шагом 10° на отрезке [0°;100°]. Построить гистограммы для синуса и косинуса. Дать названия графику, осям, добавить легенду. Построение таблиц значений функции: Правило: Построить таблицу значений sinx, cosx, tgx c шагом 10° на отрезке [0°;100°]. Построить гистограммы для синуса и косинуса. Дать названия графику, осям, добавить легенду.](https://prezentacii.org/upload/cloud/14/09/3755/images/thumbs/screen41.jpg)