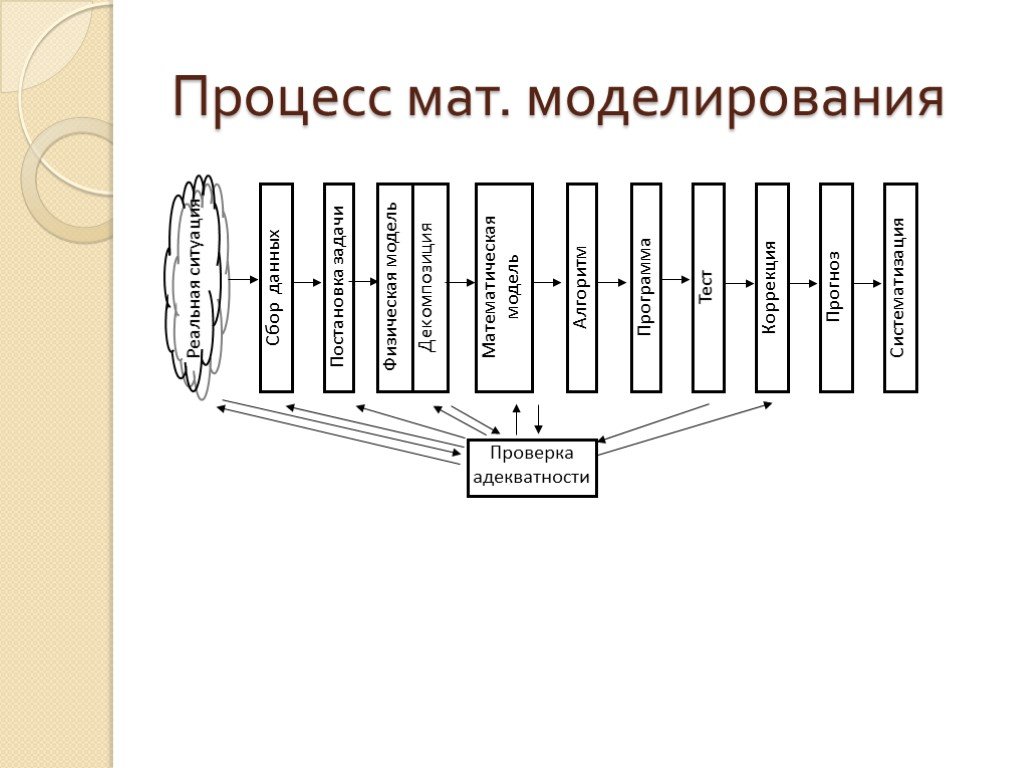
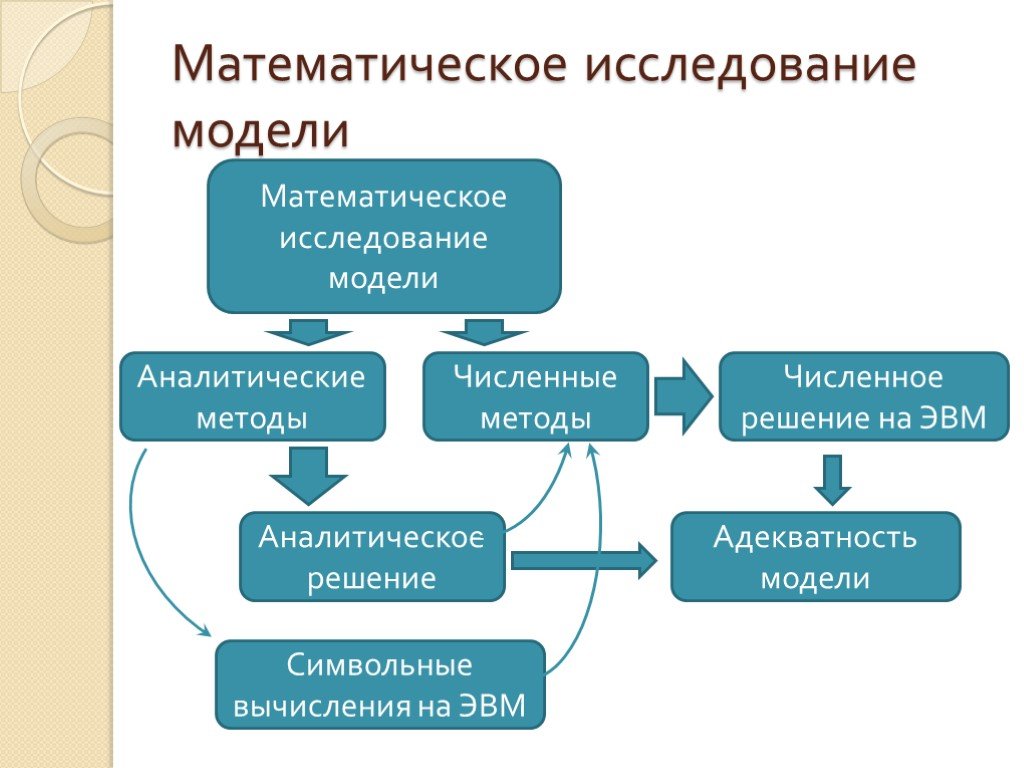
Презентация "Математическое моделирование. Численные методы и использование ЭВМ в решении прикладных задач" (7 класс) по информатике – проект, доклад

Математическое моделирование. Численные методы и использование ЭВМ в решении прикладных задач

Процесс мат. моделирования

Систематизация

Реальная ситуация

Сбор данных

Постановка задачи

Физическая модель

Декомпозиция

Математическая модель

Алгоритм Программа Тест Коррекция Прогноз

Проверка адекватности

Формулировка математической модели явления

Математическая модель любого изучаемого явления, по причине его чрезвычайной сложности, должна охватывать важнейшие для рассматриваемой задачи стороны процесса, его существенные характеристики и формализованные связи, подлежащие учёту. Как правило, математическая модель изучаемого физического явления формулируется в виде уравнений математической физики. Чаще всего это нелинейные, многомерные системы уравнений, содержащие большое число неизвестных и параметров. Если математическая модель выбрана недостаточно тщательно, то какие бы мы не применяли методы для дальнейших расчётов, полученные результаты будут ненадежны, а в отдельных случаях и совершенно неверны.

Проведение математического исследования

На этом этапе моделирования, в зависимости от сложности рассматриваемой модели, применяют различные подходы к её исследованию и различный смысл вкладывается в понятие решения задачи. Для наиболее грубых и несложных (относительно) моделей удаётся получить их аналитическое – общее – решение. Для более точных и сложных моделей основными методами решения являются численные методы решения с необходимостью требующие проведения большого объёма вычислений на ЭВМ. Эти методы позволяют добиться хорошего количественного и даже качественного результата в описании модели. Но, правда, у них есть и принципиальные недостатки – как правило, речь идёт о рассмотрении некоторого частного решения.

Математическое исследование модели

Аналитические методы

Численные методы

Численное решение на ЭВМ

Аналитическое решение

Символьные вычисления на ЭВМ

Адекватность модели

Использование ЭВМ в процессе математического исследования модели требует специфических, численных методов, т.е. такой "интерпретации" математической модели, которая может быть реализована на ЭВМ - назовём её дискретной (или вычислительной) моделью. Поскольку ЭВМ выполняет только арифметические и логические операции, то для реализации вычислительной модели требуется разработка соответствующего вычислительного алгоритма, собственно программирование, расчет на ЭВМ, обработка результатов расчета.

Источники погрешности решения

Математическая модель Исходные данные Приближенный метод Погрешности вычислений

1. Погрешность мат. модели

Математические формулировки редко точно отражают реальные явления, обычно они дают лишь более или менее идеализированные модели. Как правило, при изучении тех или иных явлений мы вынуждены допустить некоторые упрощения, что и вызывает появление погрешностей решения

2. Погрешности исходных данных

Вызваны наличием в математических формулах числовых параметров, значения которых могут быть определены лишь приближенно. Это, например, все физические константы или экспериментальные результаты, используемые в модели

3. Погрешности метода

Поскольку аналитически решить задачу невозможно, ее приходится заменять некоторой приближенной задачей, дающей близкие результаты. Например, интеграл заменяют суммой, производную – разностью, функцию – многочленом и т.д. Еще один источник – применение бесконечных итерационных процессов, принудительно прерываемых (например, sin x = x – x3/3!+x5/5! – …)

4. Погрешности вычислений

При вычислениях на ЭВМ неизбежны погрешности, связанные с ограниченностью разрядной сетки машины – погрешности округлений (dmax = 0.5a1-k, a − основание системы счисления) и с переводом чисел из одной системы счисления в другую

Числа с плавающей точкой

Современные компьютеры позволяют обрабатывать целые числа и числа с плавающей точкой. Множество целых чисел бесконечно, но из-за ограниченной разрядной сетки мы можем оперировать только с конечным подмножеством. При 4-х байтах на число диапазон доступных чисел составляет ~ от −2.109 до 2.109

При решении научно-технических задач в основном используются вещественные числа. Пример: 273.9 2739.10-1 2.739.102 0.2739.103 Последняя запись – нормализованная форма числа с плавающей точкой. Общий вид: D = ±m . 10n, m=0.d1d2… dk, d1≠0 m – мантисса, n – порядок числа

Понятие погрешности

Абсолютная погрешность – разность между истинным значением числа и приближенным. Если а – приближенное значение х: Dx = |a – x| Относительная погрешность – отношение абсолютной погрешности к приближенному значению dx = Dx/a

Предельная погрешность

Очень часто истинное значение х неизвестно и приведенные выражения невозможно использовать. В этом случае используют верхнюю оценку модуля абсолютной погрешности, называемую предельной погрешностью Dа: Dx ≤ Dа В дальнейшем Dа принимается в качестве абсолютной погрешности

Правила округления

Округление до n значащих цифр – отбрасывание всех цифр справа от n-й Если первая из отброшенных цифр меньше 5, то оставшиеся цифры остаются без изменения (8,3 ≈ 8) Если первая из отброшенных цифр больше 5, то к последней оставшейся цифре добавляется 1 (8,6 ≈ 9)

Если первая из отброшенных цифр равна 5 и среди остальных отброшенных имеются ненулевые, то к последней оставшейся цифре добавляется 1 (8,501 ≈ 9) Если первая из отброшенных цифр равна 5 и все остальные – нули, то последняя оставшаяся остается неизменной, если она четная, и увеличивается, если нечетная (6,5 ≈ 6, но 7,5 ≈ 8)

При применении правил округления погрешность не превосходит половины десятичного разряда последней оставленной цифры

Действия над приближенными числами

При сложении и вычитании чисел их абсолютные погрешности складываются: D(a ± b) = Da + Db При умножении и делении чисел их относительные погрешности складываются: d(a . b) = da + db d(a / b) = da + db При возведении числа в степень его относительная погрешность умножается на показатель степени d(ak) = kda

Пример

a = 2520, b = 2518, a – b = 2 Da = Db = 0.5 da = 0.5/2520 ≈ 0.0002 (0.02%) db = 0.5/2518 ≈ 0.0002 (0.02%) Относительная погрешность разности d(a − b) = (0.5 + 0.5)/2 = 0.5 (50%)

Уменьшение погрешностей

Избегать вычитания близких по значению чисел Применять правильный порядок вычислений Правильно использовать ряды для вычисления функций

Порядок вычислений

S = 0.2764+0.3944+1.475+26.46+1364=1393 Компьютер округляет после каждого сложения, поэтому законы коммутативности выполняются не всегда. При обратном порядке сложения получим S = 1364+26.46+1.475+0.3944+0.2764= 1391

Использование рядов

sin x= x – x3/3!+x5/5! – … sin p/6 (30º) = 0.5236-0.2392 10-1+0.3279 10-3 = 0.5 sin 13p/6 (360º+30º) = sin 6.807 ≈ 0.5167 sin 49p/6 (4x360º+30º) = sin 25.6563 ≈ 129