Конспект урока «Решение задач оптимизации в MS Excel» по информатике
Нестеренко Олеся Викторовна
Учитель математики и информатики
МАОУ СОШ №45 г. Калининграда
Решение задач оптимизации в MS Excel
Задача 2.4. Решить симплексным методом задачу о составлении рациона питания животных, условия которой приведены в задаче 1.2.
Задача 1.2. Рацион для питания животных на ферме состоит из двух видов кормов I и II. Один килограмм корма I стоит 80 ден. ед. и содержит: 1 ед. жиров, 3 ед. белков, 1 ед. углеводов, 2 ед. нитратов. Один килограмм корма II стоит 10 ден. ед. и содержит 3 ед. жиров, 1 ед. белков, 8 ед. углеводов, 4 ед. нитратов.
Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 ед., белков не менее 9 ед., углеводов не менее 8 ед., нитратов не более 16 ед.
Решение:
Представим данные, содержащиеся в условии задачи, в табличном виде.
| Число единиц питательных веществ на 1 кг корма | Необходимый минимум питательных веществ | ||
| I | II | ||
| Белки | 3 | 1 | 9 |
| Жиры | 1 | 3 | 6 |
| Углеводы | 1 | 8 | 8 |
| Нитраты | 2 | 4 | 16 (max) |
| Цена 1 кг корма, р | 80 | 10 | |
Составим экономико-математическую модель задачи. Обозначим x1, x2 − количество кормов видов I и II, входящих в рацион питания. Тогда общая стоимость рациона (целевая функция) запишется в виде Z = 80 x1 + 10 x2 .
C учетом того, что количество единиц питательных веществ, входящих в
рацион кормления, не должно быть меньше (больше) указанного минимума
(максимума), ограничения запишутся в виде следующих неравенств:
3 x1 +x 2 ≥ 9 − для белков,
x1 + 3 x 2 ≥ 6 − для жиров,
x1 + 8 x 2 ≥ 8 − для углеводов,
2 x1 + 4 x 2 ≤ 16 − для нитратов.
Кроме того, по смыслу задачи должно выполняться условие
x1 ≥ 0, x2 ≥ 0.
Таким образом, экономико-математическая модель задачи примет следующий вид: составить рацион питания, при котором достигается минимум
целевой функции:
Z ( X ) = 80 x1 + 10 x2 → min
при ограничениях:
 (1.1)
(1.1)
Приводим систему линейных неравенств (1.1) к каноническому виду, вводя в каждое неравенство дополнительную неотрицательную переменную. Получим систему линейных уравнений:
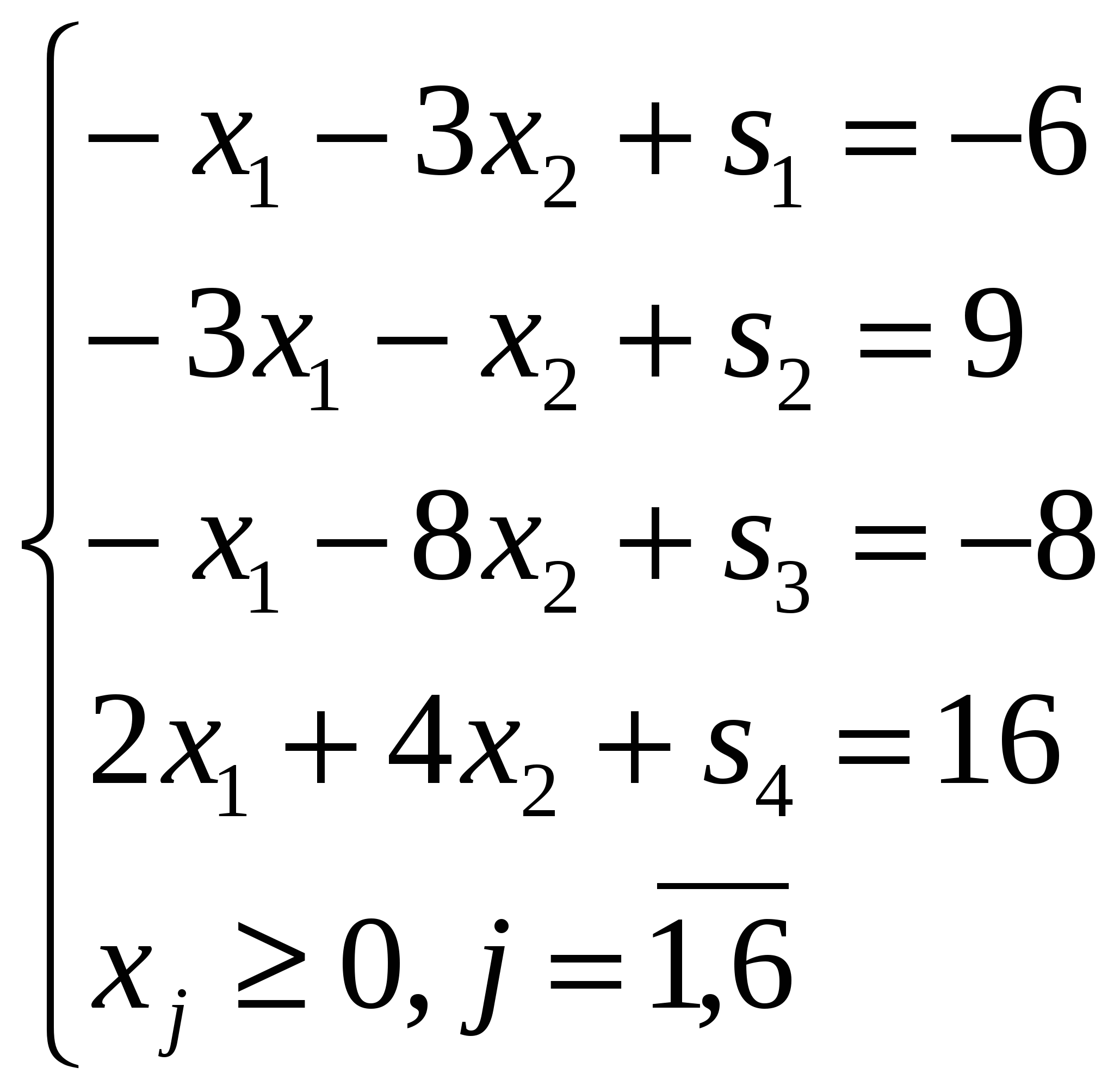 (1.2)
(1.2)
Целевая функция будет иметь вид
![]()
Векторный анализ системы ограничений:
Расширенная целевая функция:
![]()
Вектора:
| P1(x1) | P2(x2) | P3(x3) | P4(x4) | P5(x5) | P6(x6) | |
| -6 | -1 | -3 | 1 | 0 | 0 | 0 |
| -9 | -3 | -1 | 0 | 1 | 0 | 0 |
| -8 | -1 | -8 | 0 | 0 | 1 | 0 |
| 16 | 2 | 4 | 0 | 0 | 0 | 1 |
Базис:
Базисный вектор №1: x3
Базисный вектор №2: x4
Базисный вектор №3: x5
Базисный вектор №4: x6
Расширенная целевая функция:![]()
При заполнении таблицы воспользуемся следующим алгоритмом:
Алгоритм симплекс-метода
-
Задача должна быть приведена к каноническому виду. Система ограничений приведена к единичному базису, т.е. разрешена относительно некоторых базисных переменных (не умоляя общности, будем считать, что относительно первых m переменных) с помощью метода Жордана – Гаусса. Получено соответствующее исходное опорное решение
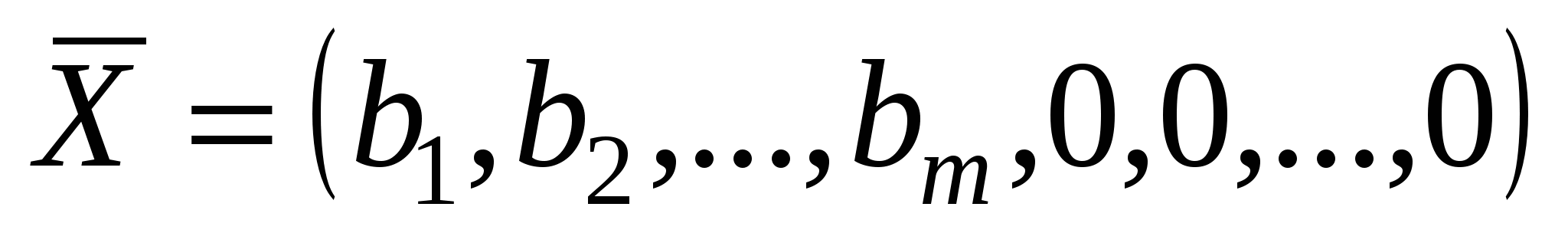 .
. -
Для удобства ведения вычислений записываем все в симплекс-таблицу (табл.). Столбец «Базис» содержит список базисных переменных; следующий столбец «cj базиса» содержит коэффициенты целевой функции при базисных переменных; следующие столбцы содержат коэффициенты системы ограничений при соответствующих переменных; столбец «bi» - столбец свободных членов системы ограничений. Последняя строка содержит симплекс – разности, рассчитанные по формуле и последняя ячейка содержит значение целевой функции
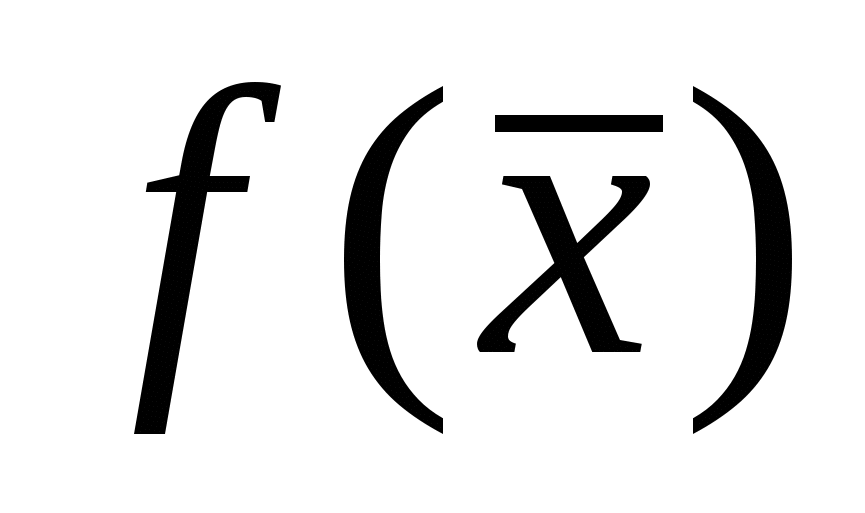 =
=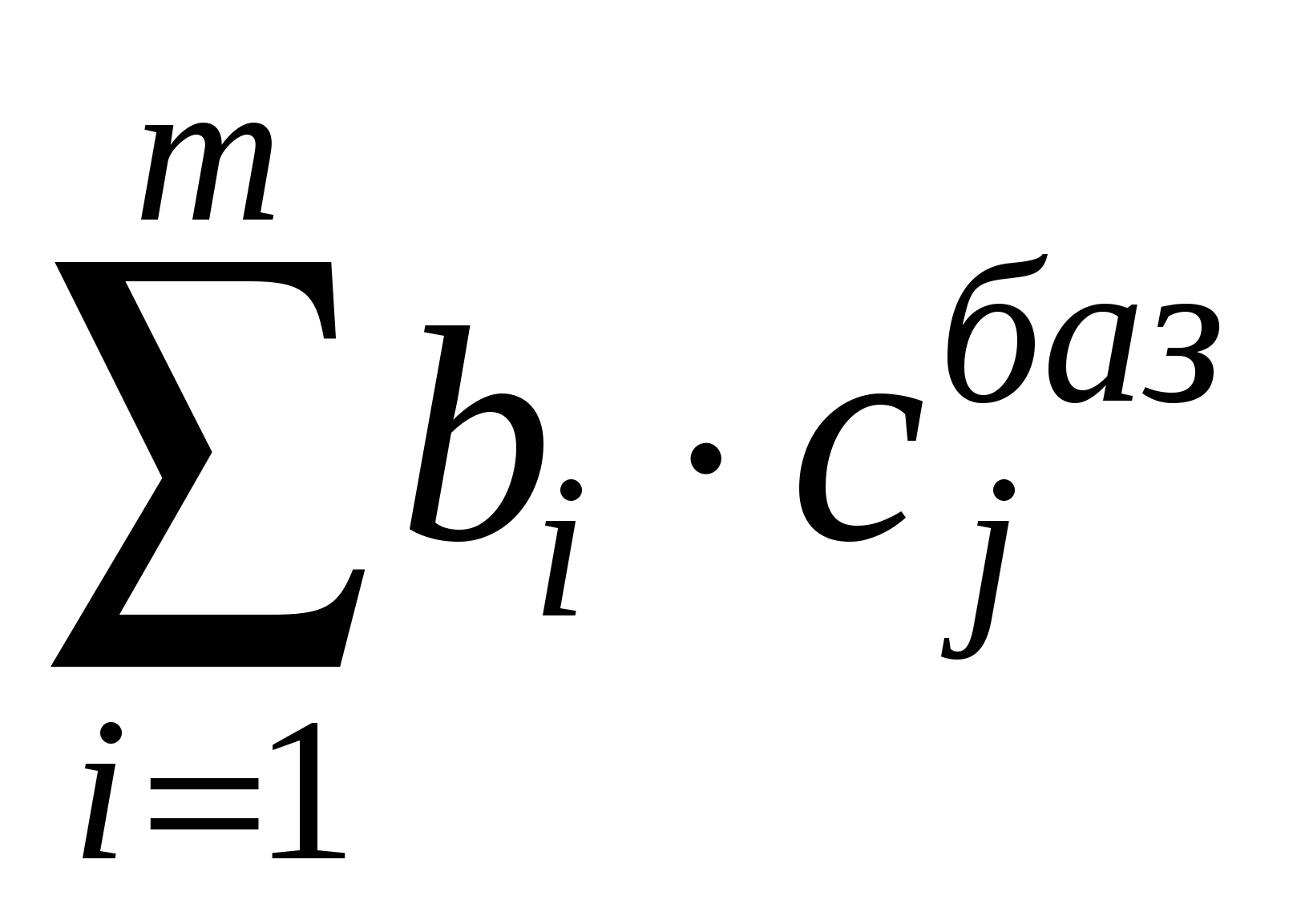 . Отметим, что симплекс – разности базисных переменных всегда равны нулю.
. Отметим, что симплекс – разности базисных переменных всегда равны нулю.
Таблица
| Базис | cj базиса | с1 | с2 | … | сm | cm+1 | … | cn | bi |
| |
| x1 | x2 | ... | xm | xm+1 | … | xn | |||||
| 1 | x1 | с1 | 1 | 0 | | 0 |
| |
|
| |
| 2 | x2 | с2 | 0 | 1 | | 0 |
| |
|
| |
| … | … | … | … | … | … | … | … | … | … | … | … |
| m | xm | сm | 0 | 0 | | 1 |
| |
|
| |
| |
|
|
| … |
|
| … |
|
| | |
-
Если все симплекс – разности неотрицательны, т.е.
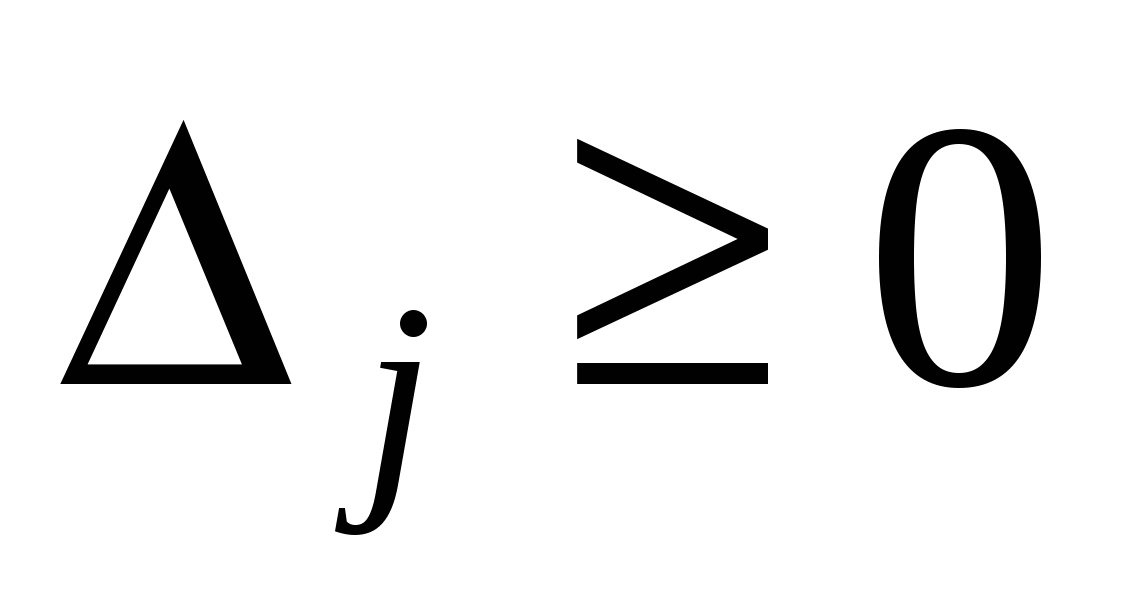 , то опорный план оптимален.
, то опорный план оптимален. -
Если хотя бы одна симплекс – разность отрицательна,
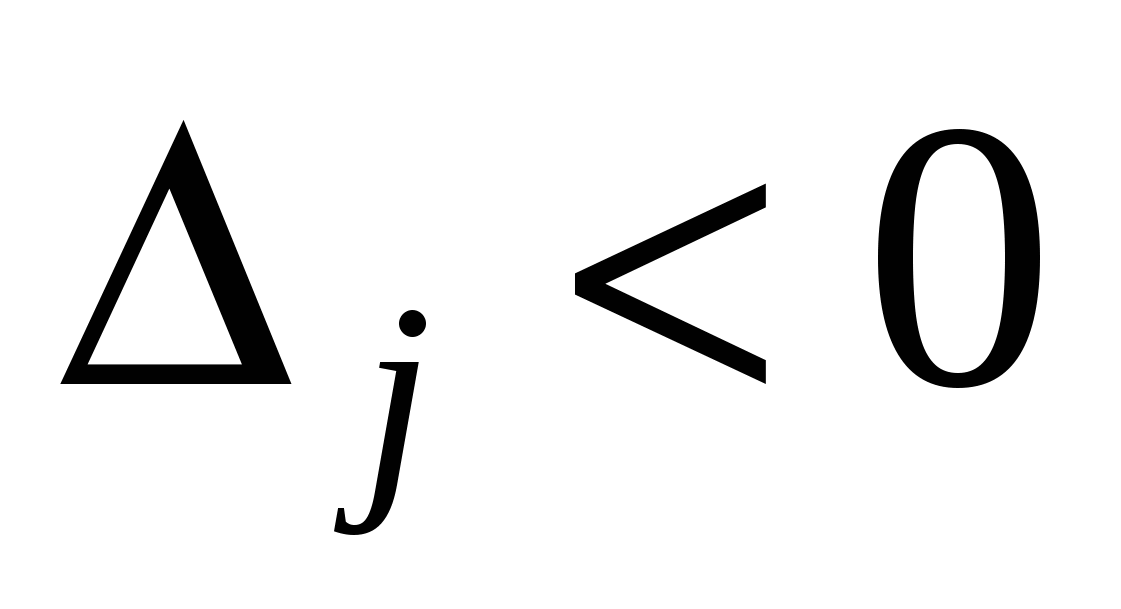 , и в соответствующем столбце нет положительных элементов, то задача не имеет оптимального решения, т.е.
, и в соответствующем столбце нет положительных элементов, то задача не имеет оптимального решения, т.е. 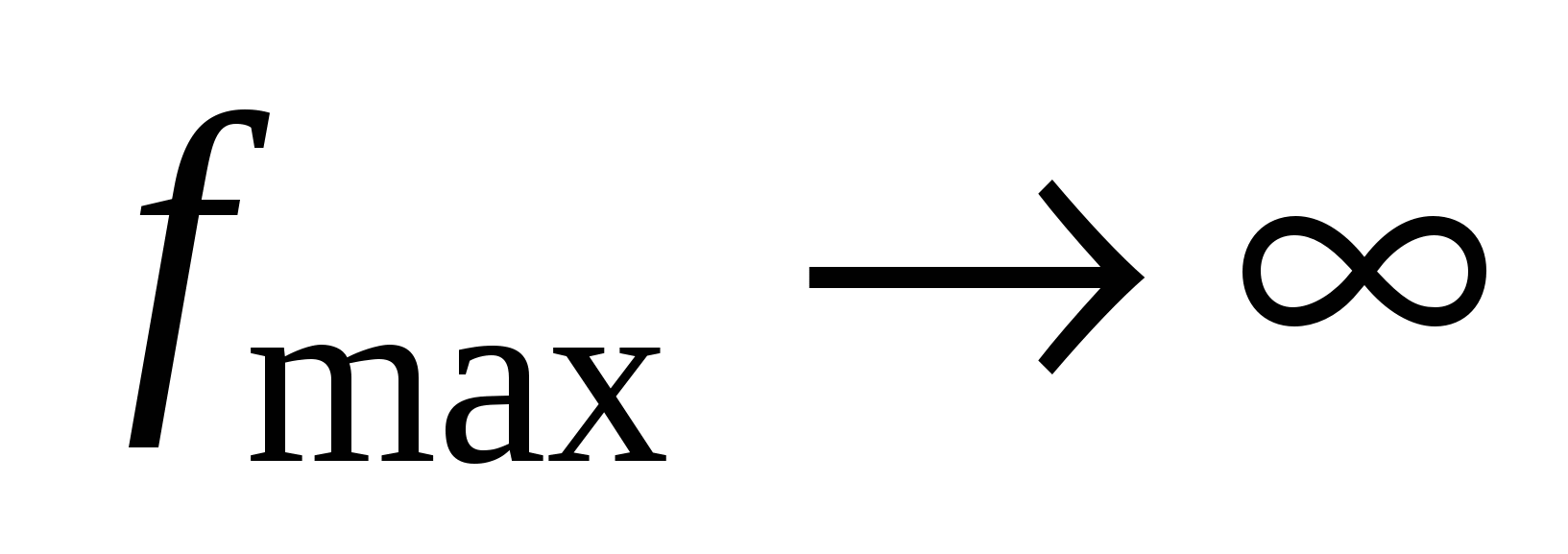 .
. -
Если хотя бы одна симплекс – разность отрицательна,
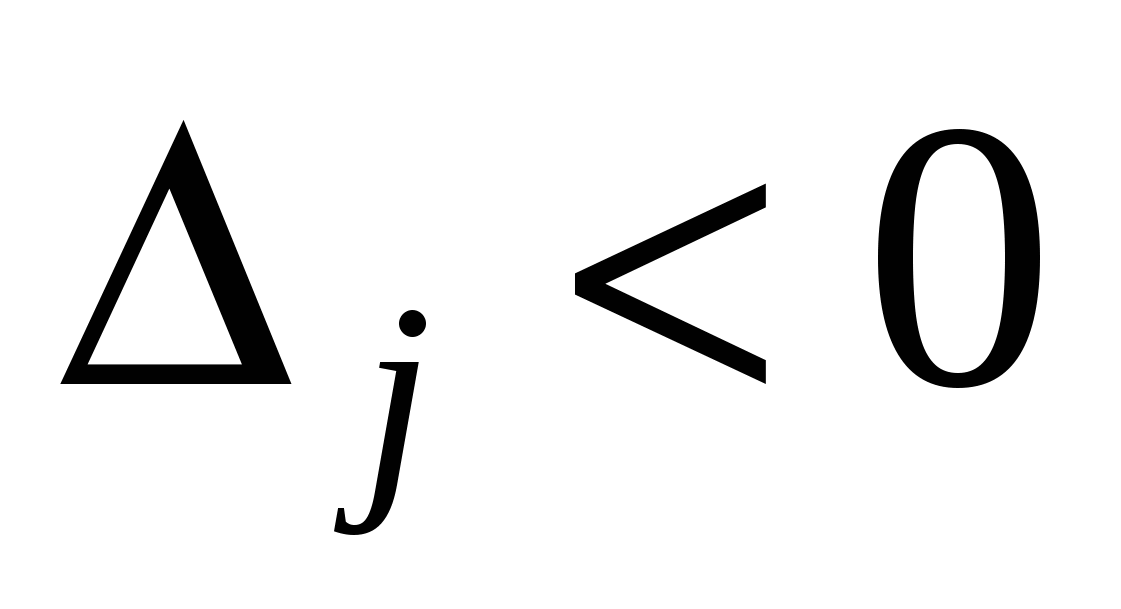 , и в каждом столбце, имеющем отрицательную оценку, есть хотя бы один положительный элемент, то полученный опорный план можно улучшить.
, и в каждом столбце, имеющем отрицательную оценку, есть хотя бы один положительный элемент, то полученный опорный план можно улучшить. -
Выбираем разрешающий столбец «р», которому соответствует наименьшая отрицательная оценка.
-
Выбираем разрешающую строку «к», которой соответствует наименьшее из отношений правых частей к соответствующим положительным элементам разрешающего столбца
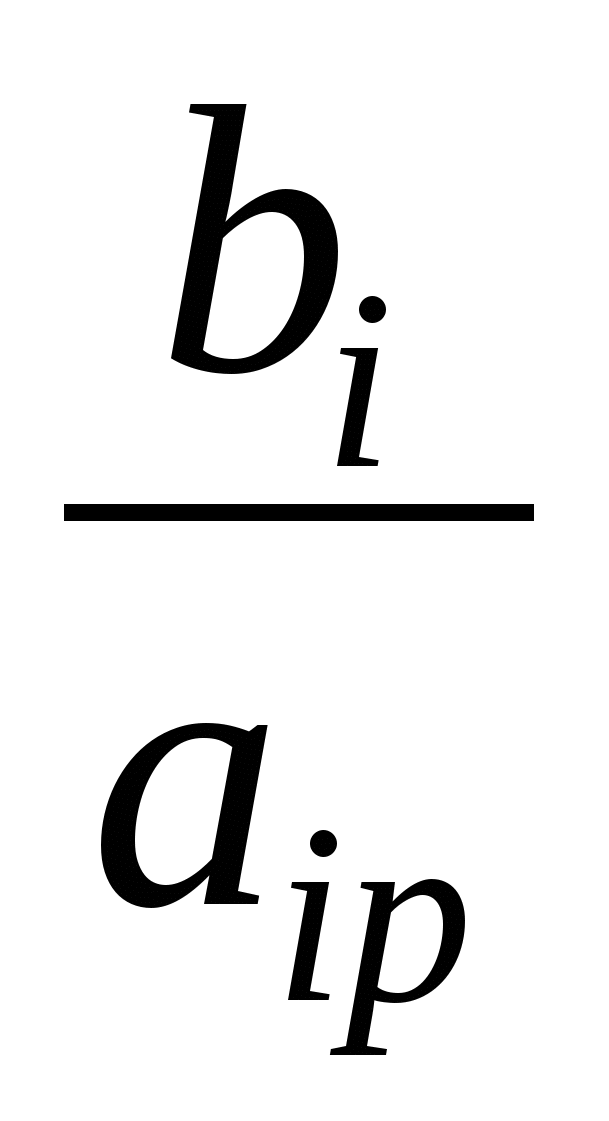 . Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки
. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки 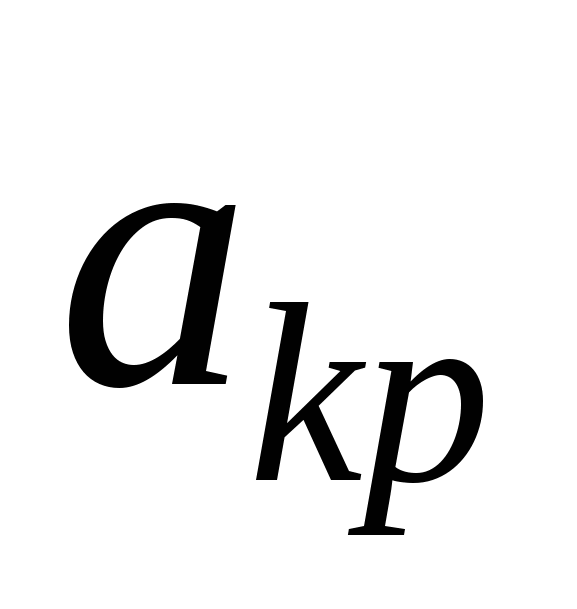 называется разрешающим элементом.
называется разрешающим элементом. -
Переходим к новой симплекс – таблице, в которой будет новый базис: базисная переменная на «к» - ом месте в старом базисе меняется на новую переменную
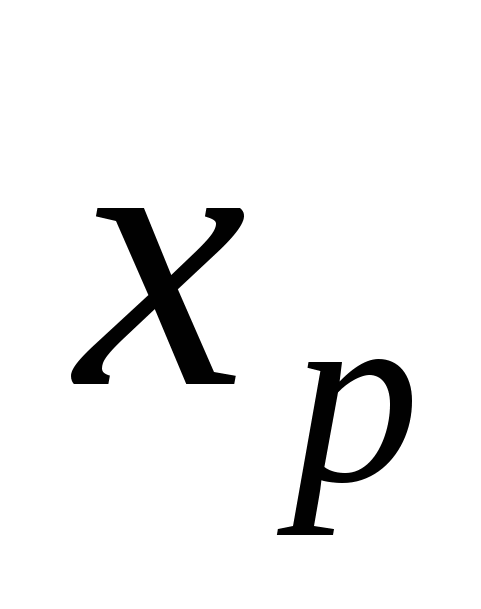 . Соответствующий вектор новой базисной переменной нужно превратить в единичный. Для этого разрешающую строку делим на
. Соответствующий вектор новой базисной переменной нужно превратить в единичный. Для этого разрешающую строку делим на 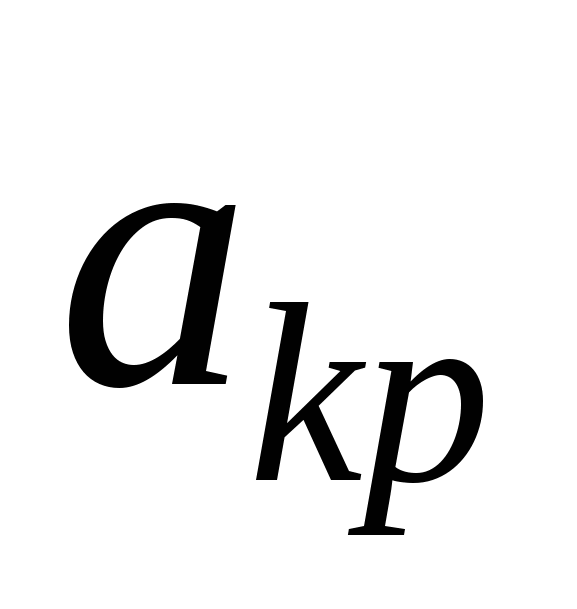 , чтобы на месте разрешающего элемента появилась единица. Умножая разрешающую строку на подходящие числа и складывая её с остальными строками получаем нули в разрешающем столбце. После этого выписываем новый опорный план и пересчитываем строчку оценок. Переходим к пункту 3.
, чтобы на месте разрешающего элемента появилась единица. Умножая разрешающую строку на подходящие числа и складывая её с остальными строками получаем нули в разрешающем столбце. После этого выписываем новый опорный план и пересчитываем строчку оценок. Переходим к пункту 3.
![]()
называется симплекс – разностью или оценкой.
Составляем симплекс – таблицу:
Таблица №1
| Базис | cj базиса | с1=80 | с2=10 | c3=0 | с4=0 | c5=0 | c6=0 | P0(bi) |
| |
| P1 | P2 | P3 | P4 | P5 | P6 | |||||
| 1 | P3 | 0 | -1 | -3 | 1 | 0 | 0 | 0 | -6 | 6 |
| 2 | P4 | 0 | - | -1 | 0 | 1 | 0 | 0 | -9 | 3 |
| 3 | P5 | 0 | -1 | 8 | 0 | 0 | 1 | 0 | -8 | 8 |
| 4 | P6 | 0 | 2 | 4 | 0 | 0 | 0 | 1 | 16 | 8 |
| |
| -80 | -10 | 0 | 0 | 0 | 0 | S min=0 | | |
Невозможно выбрать столбец замещения, так как нет положительных dj!
Выберем столбец таким образом. Чтобы избавиться от недопустимого решения, т.е. от отрицательных значений в столбце свободных членов (Р0).
Замещаемый базисный вектор: P3 (1-я строка)
Новый базисный вектор: P1 (1-й столбец)
Заменяем базисный вектор P3 на P1.
Таблица №2
| Базис | cj базиса | P0 | 80 | 10 | 0 | 0 | 0 | 0 | |
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| 1 | P1 | 80 | 6 | 1 | 3 | -1 | 0 | 0 | 0 |
| 2 | P4 | 0 | 9 | 0 | 8 | -3 | 1 | 0 | 0 |
| 3 | P5 | 0 | -2 | 0 | -5 | -1 | 0 | 1 | 0 |
| 4 | P6 | 0 | 4 | 0 | -2 | 2 | 0 | 0 | 1 |
| S min = | 480 | 0 | 230 | -80 | 0 | 0 | 0 | ||
| | | | | | | | |||
Замещаемый базисный вектор: P5 (3-я строка)
Новый базисный вектор: P2 (2-й столбец)
Заменяем базисный вектор P5 на P2.
Таблица №3
| Базис | cj базиса | P0 | 80 | 10 | 0 | 0 | 0 | 0 | |
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| 1 | P1 | 80 | 4,8 | 1 | 0 | -1,6 | 0 | 0,6 | 0 |
| 2 | P4 | 0 | 5,8 | 0 | 0 | -4,6 | 1 | 1,6 | 0 |
| 3 | P2 | 10 | 0,4 | 0 | 1 | 0,2 | 0 | -0,2 | 0 |
| 4 | P6 | 0 | 4,8 | 0 | 0 | 2,4 | 0 | -0,4 | 1 |
| S min = | 388 | 0 | 0 | -126 | 0 | 46 | 0 | ||
| | | | | | | | |||
Замещаемый базисный вектор: P4 (2-я строка)
Новый базисный вектор: P5 (5-й столбец)
Заменяем базисный вектор P4 на P5.
Таблица №4
| Базис | cj базиса | P0 | 80 | 10 | 0 | 0 | 0 | 0 | |
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| 1 | P1 | 80 | 2,625 | 1 | 0 | 0,125 | -0,375 | 0 | 0 |
| 2 | P5 | 0 | 3,625 | 0 | 0 | -2,875 | 0,625 | 1 | 0 |
| 3 | P2 | 10 | 1,125 | 0 | 1 | -0,375 | 0,125 | 0 | 0 |
| 4 | P6 | 0 | 6,25 | 0 | 0 | 1,25 | 0,25 | 0 | 1 |
| S min = | 221,25 | 0 | 0 | 6,25 | -28,75 | 0 | 0 | ||
| | | | | | | | |||
Замещаемый базисный вектор: P6 (4-я строка)
Новый базисный вектор: P3 (3-й столбец)
Заменяем базисный вектор P6 на P3.
Таблица №5
| Базис | cj базиса | P0 | 80 | 10 | 0 | 0 | 0 | 0 | |
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| 1 | P1 | 80 | 2 | 1 | 0 | 0 | -0,4 | 0 | -0,1 |
| 2 | P5 | 0 | 18 | 0 | 0 | 0 | 1,2 | 1 | 2,3 |
| 3 | P2 | 10 | 3 | 0 | 1 | 0 | 0,2 | 0 | 0,3 |
| 4 | P3 | 0 | 5 | 0 | 0 | 1 | 0,2 | 0 | 0,8 |
| S min = | 190 | 0 | 0 | 0 | -30 | 0 | -5 | ||
| | | | | | | | |||
Невозможно выбрать столбец замещения, так как нет положительных dj!
Получено оптимальное решение.
| x2 | x3 | x4 | x5 | x6 | |
| 2 | 3 | 5 | 0 | 18 | 0 |
Целевая функция:
S min = 80·2+10·3
И в результате:
S min = 190;
Ответ: x1=2; х2=3- количество кормов I, II, входящих в рацион питания. Общая стоимость рациона (целевая функция) при котором достигается минимум целевой функции равен 190.
Решение задачи с помощью MS EXCEL
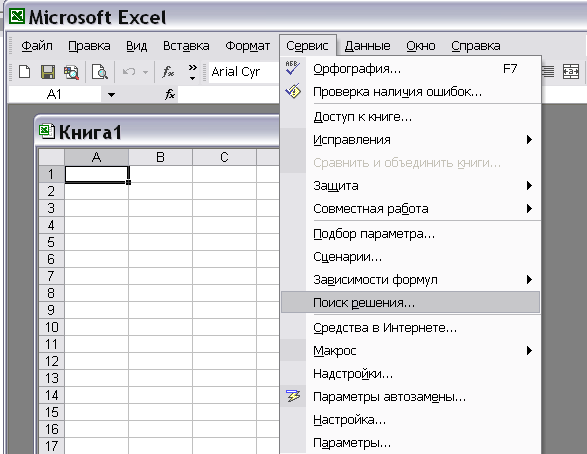
Для решения задач оптимизации в MS Excel используют надстройку Поиск решения, которая вызывается из пункта главного меню «Сервис» (рис. 1).
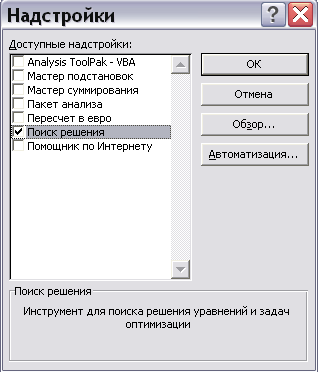
Если в версии Excel, установленной на Вашем компьютере, отсутствует данный подпункт меню «Сервис», необходимо вызвать пункт меню «Надстройки» и в предложенном списке дополнительных модулей выбрать «Поиск решения» (рис. 2).
| Рис. 2 |
Рассмотрим использование данной надстройки на примере. Решим с её помощью задачу, математическая модель которой строилась. Математическая модель задачи имеет вид:
целевой функции:
Z ( X ) = 80 x1 + 10 x2 → min
при ограничениях:
 Составим шаблон в редакторе Excel, как показано на рис. 3
Составим шаблон в редакторе Excel, как показано на рис. 3
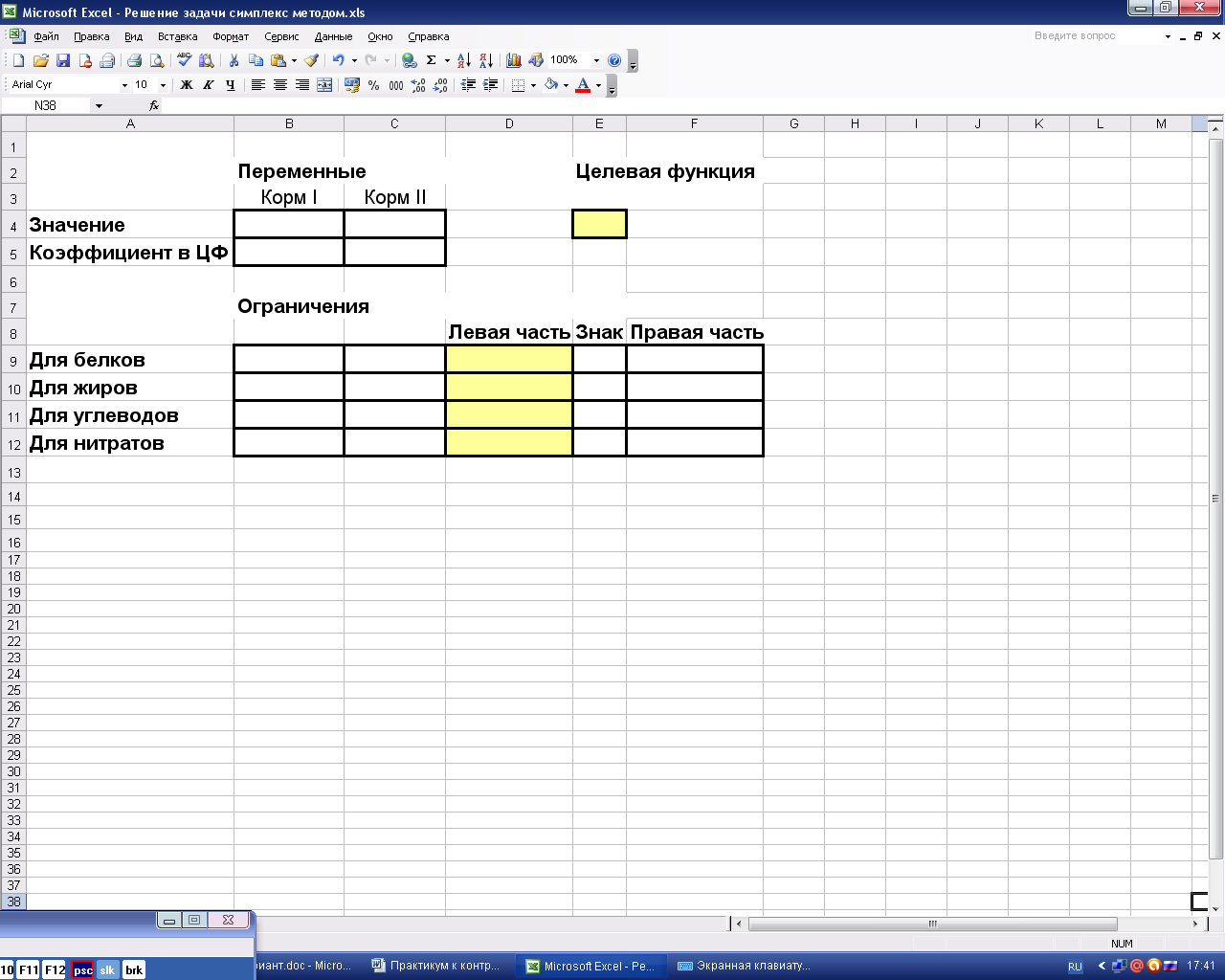
Рис.3. Шаблон оформления задачи
Теперь занесём данную в задаче числовую информацию (рис. 4).
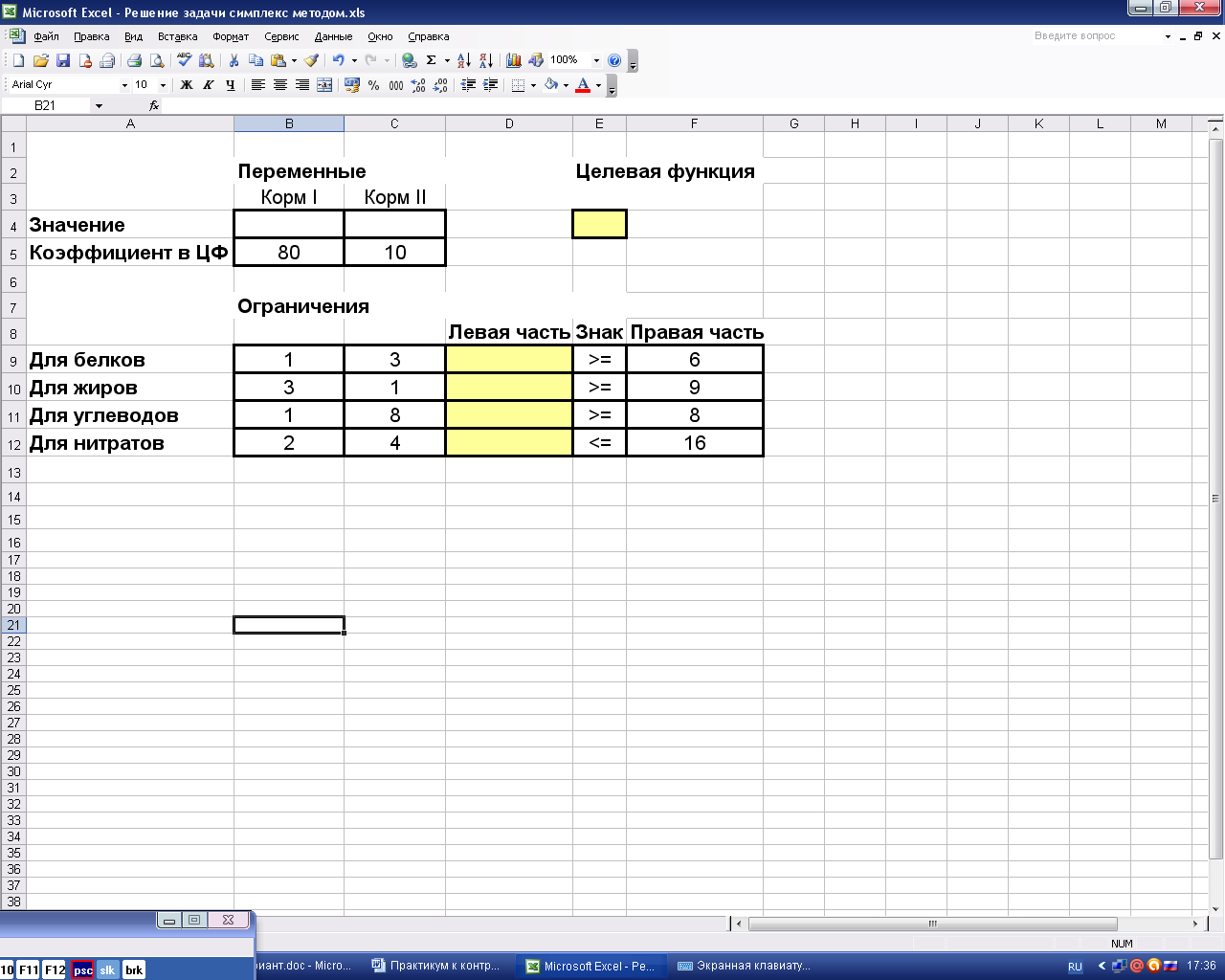
Рис.4. Исходные данные задачи
В выделенные пустые ячейки (значения целевой функции и левых частей неравенств) необходимо занести формулы, отображающие связи и отношения между числами на рабочем листе.
Ячейки B4 – С4 называются в Excel изменяемыми (в нашей модели это неизвестные переменные), т.е., изменяя их Поиск решения будет находить оптимальное значение целевой функции. Значения, которые первоначально вводят в эти ячейки, обычно нули (незаполненные клетки трактуются по умолчанию как содержащие нулевые значения).
Теперь необходимо ввести формулы. В нашей математической модели, целевая функция представляет собой произведение вектора коэффициентов на вектор неизвестных. Действительно, выражение ![]() можно рассматривать как произведение вектора (80,10) на вектор (Х1,Х2).
можно рассматривать как произведение вектора (80,10) на вектор (Х1,Х2).
В Excel существует функция СУММПРОИЗВ, которая позволяет найти скалярное произведение векторов. В ячейку Е4 необходимо вызвать данную функцию, а в качестве перемножаемых векторов задать адреса ячеек, содержащих коэффициенты уравнений (в данном случае, это В5:С5) и ячеек, в которые в результате решения будут помещены значения Х1 и Х2 (ячейки В4:С4) (рис. 5).
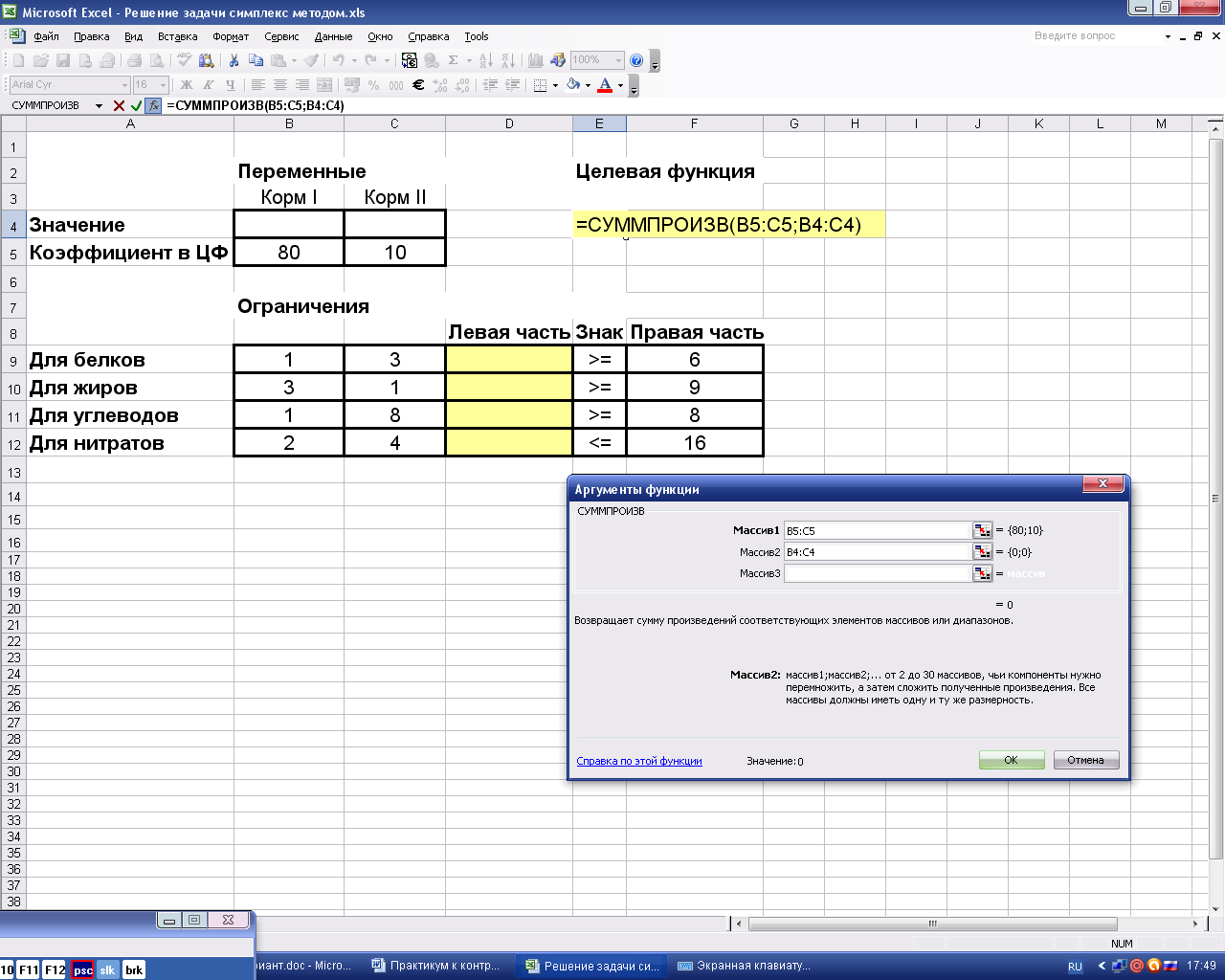
Рис.5. Вызов функции СУММПРОИЗВ.
Каждая левая часть ограничения тоже представляет собой произведение двух векторов: соответствующей строки матрицы затрат и вектора неизвестных. То есть, выражение Х1+3Х2 (для первого ограничения Х1 + 3Х2 ![]() 6) будем рассматривать как произведение вектора коэффициентов (1,3) и вектора переменных (Х1,Х2).
6) будем рассматривать как произведение вектора коэффициентов (1,3) и вектора переменных (Х1,Х2).
В ячейке, отведенной для формулы левой части первого ограничения (D9), вызовем функцию СУММПРОИЗВ. В качестве адресов перемножаемых векторов занесем адрес строки коэффициентов В9:С9 и адрес значений переменных В4:С4 (рис. 6).
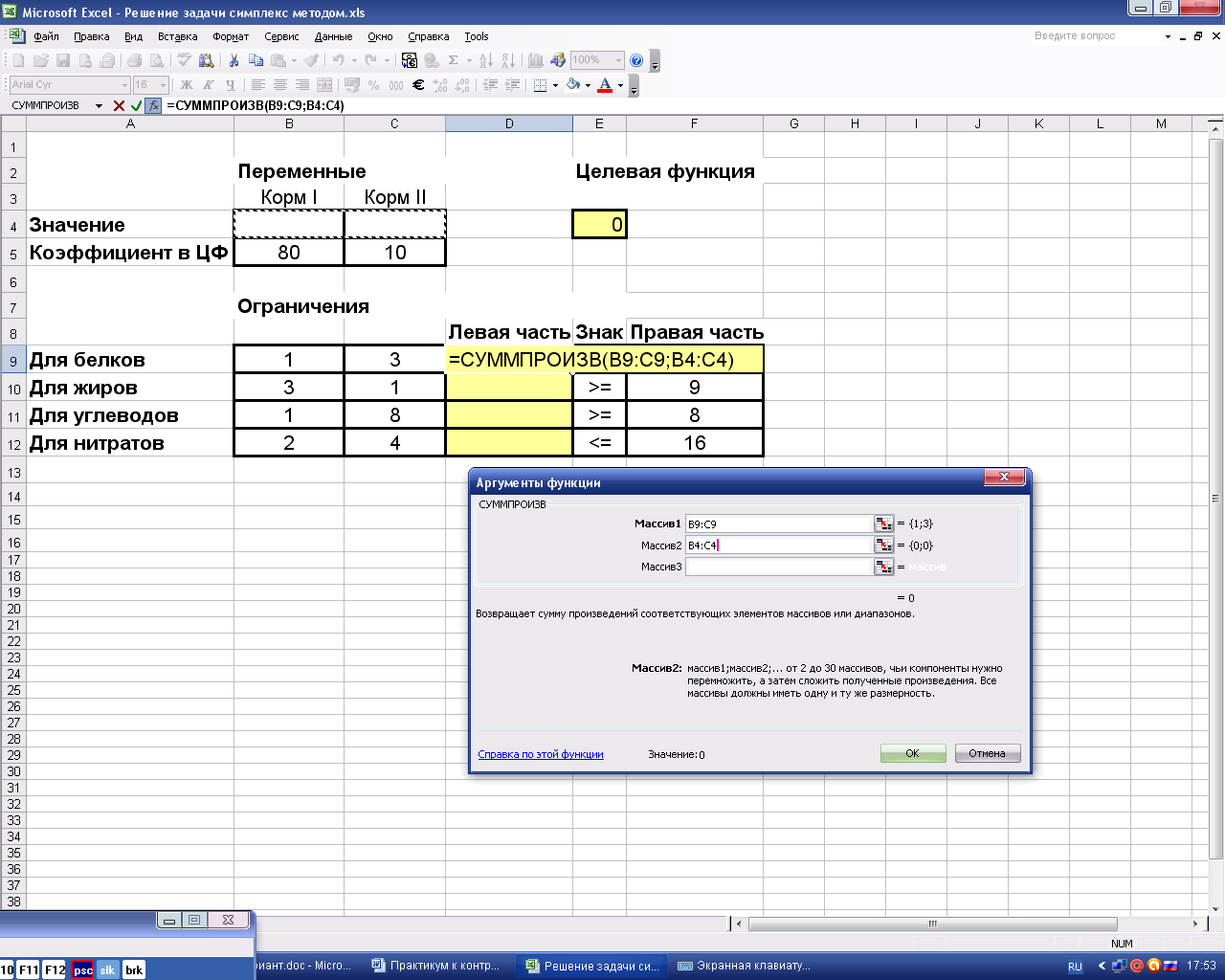
Рис.6
В четыре оставшиеся ячейки графы «Левая часть» вводим аналогичные формулы, используя соответствующую строку матрицы затрат. Фрагмент экрана с введёнными формулами показан на рис.7.
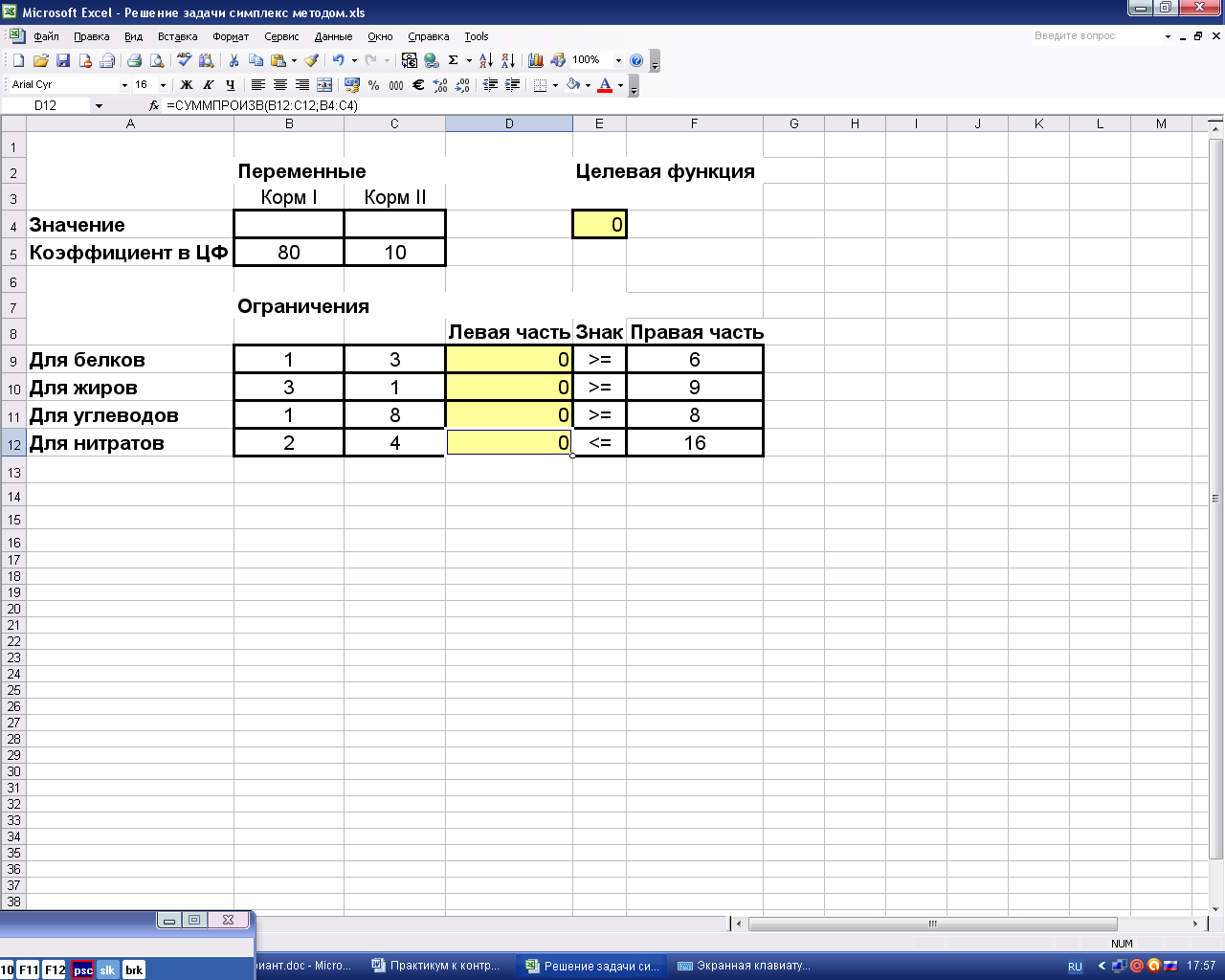
Рис.7
Важно, чтоб к моменту вызова сервиса «Поиск решения» на рабочем листе с задачей должны быть занесены формулы для левых частей ограничений и формула для значения целевой функции.
В меню Сервис выбираем Поиск решения. В появившемся окне задаём следующую информацию:
-
в качестве целевой ячейки устанавливаем адрес ячейки для значения целевой функции Е4;
-
«флажок» устанавливаем на вариант «максимальному значению», т.к. в данном случае, целевая функция дохода подлежит максимизации;
-
в качестве изменяемых ячеек заносится адрес строки значений переменных В4:С4;
-
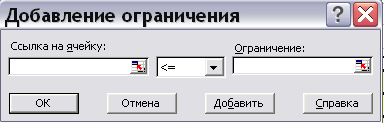
справа от окна, предназначенного для занесения ограничений, нажимаем кнопку «Добавить», появится форма для занесения ограничения (рис. 8)
|
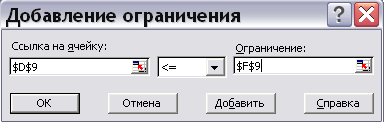
Рис.9 Занесение первого ограничения задачи |
-
в левой части формы «Ссылка на ячейку» заносится адрес формулы для левой части первого ограничения D9, выбирается требуемый знак неравенства (в нашем случае, F9 (рис. 9).
-
аналогично заносятся все ограничения задачи, после чего нажимается кнопка «ОК».
Таким образом, окно «Поиск решения» с занесенной информацией выглядит следующим образом (рис.10):

Рис.10.
Далее необходимо нажать кнопку Параметры, установить «флажки» «Линейная модель» и «Неотрицательные значения», поскольку в данном случае задача является ЗЛП, а ограничение 6) требует неотрицательности значений (рис.11).
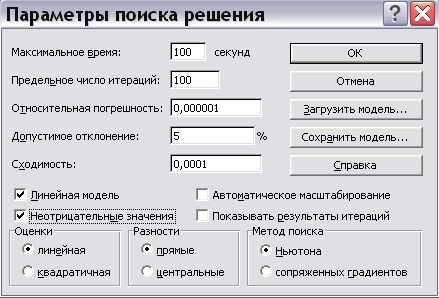
Рис.11 Установка параметров
Затем следует нажать «ОК», «Выполнить», после чего появляется окно результата решения (рис.12).

Рис.12. Окно результата решения
Если в результате всех действий получено окно с сообщением «Решение найдено», то Вам предоставляется возможность получения трех типов отчета, которые полезны при анализе модели на чувствительность. В данном примере достаточно сохранить найденное решение, нажав «ОК». В результате получено решение задачи из примера 1. (рис.13).

Рис.13 Результат применения «Поиска решения»
Если в результате решения задачи выдано окно с сообщением о невозможности нахождения решения (рис.14), это означает, что при оформлении задачи была допущена ошибка (не заполнены формулы для ограничений, неправильно установлен «флажок» максимизации/минимизации и т.д.).

Рис.14. Сообщение об ошибке
В данном разделе рассмотрен общий формат решения задач оптимизации в Excel. В зависимости от экономических моделей, выполняют его соответствующие модификации.
Ответ: x1=2; х2=3- количество кормов I, II, входящих в рацион питания. Общая стоимость рациона (целевая функция) при котором достигается минимум целевой функции равен 190.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
-
Высшая математика для экономистов / Под ред. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.
-
Горчаков А.А., Орлова И.В. Компьютерные экономико - математические модели. – М.: Компьютер, ЮНИТИ, 1995.
-
Ерохин Н.М., Орехов Н.А., Сидоренко А.В. Статистические модели и планирование экспериментов в экономике: Методическое пособие. – Калуга: КФ МГТУ, 1994.
-
Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М., 1997.
-
Исследование операций / Под ред. М.А. Войтенко и Н.Ш. Кремера. – М.: Экономическое образование, 1992.
-
Исследование операций в экономике: Учебное пособие для вузов / Н.Ш. Кремер, Б.А. Путко, И.М., И.М. Тришин, М.Н. Фридман; под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2004.
-
Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. – Минск: Вышэйшая школа, 1994.
-
Математическое программирование / Под ред. Н.Ш. Кремера. – М.: Финстатинформ, 1995.
-
Орехов Н.А., Левин А.Г., Горбунов Е.А. Математические методы и модели в экономике: Учебное пособие для вузов / Под ред. проф. Н.А. Орехова. – М.: ЮНИТИ-ДАНА, 2004.
-
Орехов Н.А., Сахаров Г.В., Карпушин А.А. Введение в моделирование экономических процессов и явлений. – Калуга: КФ МГЭИ, 1997.
-
Сборник задач и упражнений по высшей математике: математическое программирование / Под ред. А.В. Кузнецова. – Минск: Высшая школа, 1995.
-
Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.
Здесь представлен конспект к уроку на тему «Решение задач оптимизации в MS Excel», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Информатика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

 3
3