Презентация "Применение систем счисления" по информатике – проект, доклад
Презентацию на тему "Применение систем счисления" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).
Слайды презентации
Список похожих презентаций
Компьютерные системы счисления
Проверка домашней работы:. РТ. № 41 (визуально) № 55(3), 56(3)( у доски) №46(устно). По 1 баллу. Где применяется двоичная система счисления? Каков ...Представление числовой информации в различных системах счисления
Числа не управляют миром, но показывают, как управляется мир. Иоганн Гёте. Системы счисления. Это совокупность примеров и правил для обозначения и ...Представление числовой информации с помощью систем счисления
Управление презентацией. Переход по слайдам осуществляется с помощью управляющих кнопок и гиперссылок Возврат в содержание осуществляет кнопка Окончание ...Представление числовой информации с помощью систем счисления
Задачи урока. Сформировать у учащихся понятие системы счисления, позиционной и не позиционной системы счисления. Сформировать у учащихся понятие основание ...Представление целого числа в позиционных системах счисления
Задачи: показать теоретические знания основных понятий, научиться переводить числа в различные системы счисления. Вопросы викторины: Что такое система ...Представление чисел в различных системах счисления
Система счисления – определенные правила записи чисел и связанные с ними способы выполнения вычислений. Алгоритм записи развернутой формы числа десятичной ...Перевод числа из десятичной системы счисления в другую позиционную систему
Перевести числа из недесятичной системы счисления в десятичную. Тема урока: «Перевод числа из десятичной системы счисления в другую позиционную систему». ...Двоичная система счисления
Жил-был Ежик. Он был очень хорошим. У него было 10000000 друзей по всему лесу. Но особенно он дружил с 10 белочками. Ежик любил гулять по лесу. Особенно ...Двоичная система счисления
Вспомните степени числа. Запишите ответы в тетрадях. 5 2 0 7 10 4 8. Перевод десятичных чисел в двоичную систему счисления. 29 2 14 28 1 7 0 6 2910=111012. ...Девять предметов в системе счисления
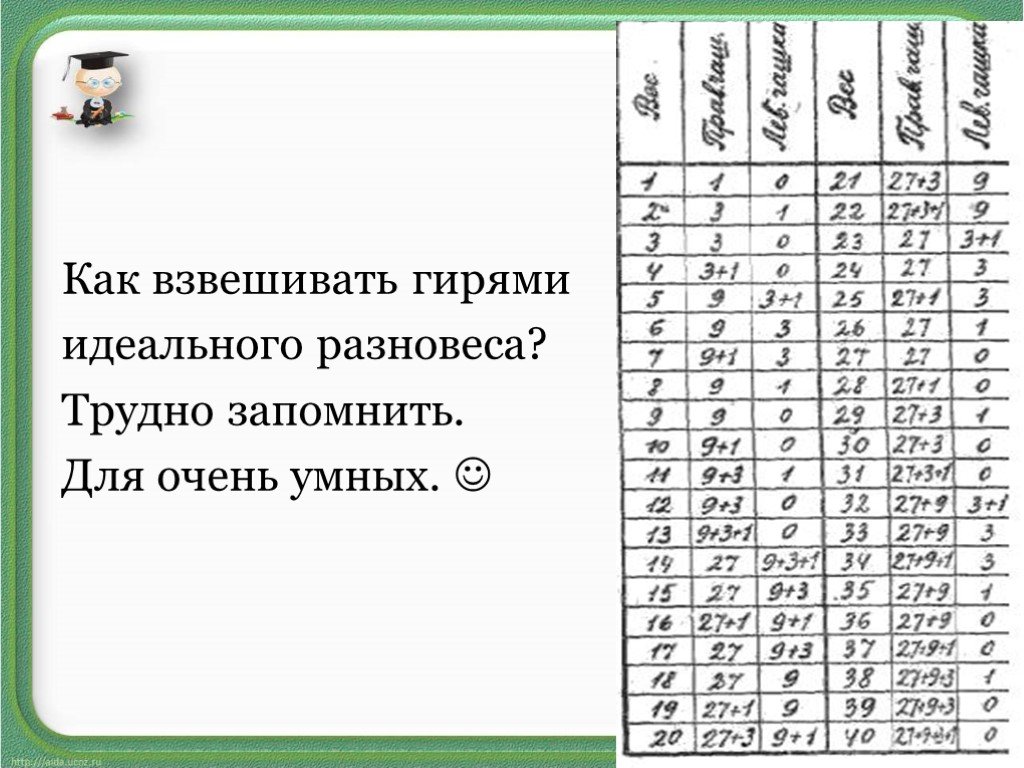
"Все есть число". Говорили древнегреческие философы, ученики Пифагора, подчеркивая важную роль чисел в практической деятельности. Эпиграф. Девять ...Двоичная система счисления
Цитаты. Всё наше достоинство заключено в мысли… Будем же учиться хорошо мыслить. Б. Паскаль Учение без размышления бесполезно, но и размышление без ...Переход от двоичной системы счисления к восьмеричной
Цели урока: ознакомить учащихся с правилом перевода чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную; ознакомить учащихся с ...Перевод чисел из одной системы счисления в другую
При записи чисел указывают основание системы счисления:. 10 1100 645 16. Двести тридцать четыре. Один – один – ноль - ноль по основании два. Шесть ...Перевод из 10-ной системы счисления в N-ую
Перевод целой части числа. Делим исходное число на основание новой системы счисления: получаем целую часть от деления и остаток. 67 : 2 = 33 (остаток ...Перевод целых чисел в двоичную систему счисления
Цель урока:. Перевод десятичных чисел в двоичную систему счисления и обратно. Узнать и освоить способы перевода целых чисел из десятичной системы ...Информация и информационные процессы. Измерение информации. Системы счисления
Задание № 1. Что из ниже перечисленного не является для вас информацией? а) LIRO CAS. в) Лед – твердое вещество. г) 25 · 15 = 360. б) Сегодня на улице ...Перевод из десятичной системы счисления в произвольную
1. Перевод из 10-ной сс в произвольную. Правило: Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно ...Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную
Таблица цифр. Правило Данное двоичное число разбить справа налево на группы по 3 цифры в каждой Если в последней левой группе окажется меньше 3 цифр, ...Перевод десятичных чисел в другие системы счисления
Цели:. познакомить с алгоритмами перевода десятичных чисел в двоичную, восьмеричную, шестнадцатеричную и др. системы счисления; способствовать закреплению ...Конспекты
Арифметические операции в позиционных системах счисления
Арифметические операции в позиционных системах счисления. Цель урока:. формирование умения выполнять Арифметические операции в позиционных системах ...Арифметические операции в позиционных системах счисления
ПЛАН-КОНСПЕКТ УРОКА. Источник и приемник информации. ФИО (полностью): Усольцева Юлия Владимировна. . . Место работы:. Владимирская обл., ...Арифметические операции в позиционных системах счисления
5. . Тема:. . «Арифметические операции в позиционных системах счисления». Цели урока:. содействовать ознакомлению учащихся с правилами ...Перевод чисел в позиционных системах счисления
Разработка урока информатики в 10 классе учитель Шевченко О.В. Тема урока:. ". . Перевод чисел в позиционных системах счисления. ". . Цели:. ...Шестнадцатеричная система счисления. Операции над числами в двоичной системе счисления
ИНФОРМАТИКА 1 курсы 1 семестр. Раздел «Информация» Системы счисления. ______________________________________________________________________________________________________. ...Перевод чисел из десятичной системы счисления в любую другую
ПЛАН-КОНСПЕКТ УРОКА. «Перевод чисел из десятичной системы счисления в любую другую». . ФИО (полностью). . Помыкалова Елена Викторовна. ...Арифметические действия в двоичной системе счисления
Урок «Арифметические действия в двоичной системе счисления». Это 4-й урок в блоке уроков «Табличные вычисления на компьютере», урок №2 в теме ...Системы счисления
. МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БАШКОРТОСТАН. ОТДЕЛ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ ГОРОДА СТЕРЛИТАМАК. МАОУ «СОШ № 24». ...Перевод чисел из любой системы счисления в десятичную
Конспект урока по информатике на тему: «Перевод чисел из любой системы счисления в десятичную». Цели:. дидактическая:. дать понятие разряда, разобрать ...Двоичная система счисления
ОГБОУ СО СПО «Ульяновский техникум железнодорожного транспорта». Методическая разработка. . открытого урока по дисциплине. «Информатика». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 мая 2019
Категория:Информатика
Содержит:25 слайд(ов)
Поделись с друзьями:
Скачать презентацию