Конспект урока «Квадратный корень из произведения и дроби» по математике для 8 класса
Козлова Лидия Николаевна
учитель математики
Тенистовская общеобразовательная школа I-III ступеней
Бахчисарайского района
Республика Крым
ПЛАН-КОНСПЕКТ УРОКА
Квадратный корень из произведения и дроби
(Тема урока)
Аннотация к уроку: Урок в 8 классе по теме «Квадратный корень из произведения и дроби» соответствует программе, учебник Макарычева Ю.Н.. Это комбинированный урок. На уроке используются различные методы: актуализация знаний, проблемное обучение, тестовая работа, групповая работа, самостоятельная работа.
| ФИО (полностью) | Козлова Лидия Николаевна | |
| | Место работы | Тенистовская СОШ |
| | Должность | Учитель математики |
| | Предмет | Алгебра |
| | Класс | 8 |
| | Тема и номер урока | Квадратные корни. |
| | Базовый учебник | Алгебра 8 : учебник для 8 кл. образоват. учреждений/ Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова – М.: Просвещение, 2010. |
Цели урока:
Образовательные:
- изучить основные свойства квадратных корней,
- сформировать умение применять их для преобразования выражений, содержащих квадратные корни,
- научить вычислять значения квадратных корней.
Воспитательные:
- воспитывать внимательность, аккуратность, настойчивость.
- воспитывать интерес к математике.
Развивающие:
- развивать память,
- развивать умений преодолевать трудности,
- развивать логическое мышление
- развивать навыки работы с учебником, справочными материалами.
Задачи:
в направлении личностного развития:
- уметь ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи;
- воспитание способности принимать самостоятельные решения;
- уметь осознавать и понимать личную ответственность за будущий результат;
в метапредметном направлении:
-уметь использовать математическую терминологию;
- уметь использовать эталон для самопроверки;
- уметь воспринимать устную речь;
в предметном направлении:
- владеть математическими знаниями и умениями, необходимыми для продолжения образования;
- уметь использовать математическую терминологию;
-уметь применять теоремы о квадратных корнях из произведения и дроби для вычисления значений выражений, содержащих квадратные корни.
Оборудование:
таблица квадратов натуральных чисел, материалы для самостоятельных работ.
Тип урока:
комбинированный.
ХОД УРОКА.
I . Организационный момент. Проверка домашнего задания.
Квадратные корни широко используются во многих областях: в геометрии, в физике и т. д. Приведите примеры.
II. Актуализация опорных знаний
-
Сформулируйте определение квадратного корня
-
Сформулируйте определение арифметического квадратного корня
-
Верно ли равенство:
а). ![]() = – 10 (нет)
= – 10 (нет)
б). ![]() = 2.4 (нет)
= 2.4 (нет)
в). – ![]() = – 0,5 (да)
= – 0,5 (да)
г). ![]() = – 4 (нет)
= – 4 (нет)
д). ![]() = 660 (да)
= 660 (да)
4. «Расшифруй слово»
Вычисли правильно и узнай, что необходимо на уроке.
-
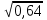 г) 0,4; з) 0,8.
г) 0,4; з) 0,8. -
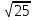 и) 12; о) 0,2.
и) 12; о) 0,2. -
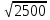 с) 3500; а) 50.
с) 3500; а) 50. -
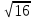 +1 н) 5; п) 9.
+1 н) 5; п) 9. -
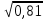 и) 0,9; у) 1
и) 0,9; у) 1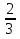 .
. -
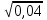 к) 0,4; я) 4.
к) 0,4; я) 4.
(знания)
Работая устно обучающиеся формируют умения:
Л. - понимать смысл поставленной задачи;
Л. - самостоятельно контролировать своё время и управлять им;
М. - воспринимать устную речь.
5. Вычислите
. 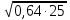
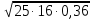
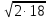 .
.
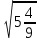
При решении сталкиваются с проблемой: Как вычислить корень из произведения и дроби?
Оказывается, в ответе должно получится натуральное число, но чтобы его получить, нам необходимы новые знания. Как вы думаете, какие же именно?
Формируют умения:
М. - прилагать волевые усилия и преодолевать трудности и препятствия на пути достижения целей.
III. Изучение новой темы.
1. Чему же равен квадратный корень из произведения?
– Корень из произведения неотрицательных множителей равен произведению корней из этих множителей:
а > 0, b > 0, ![]() =
= ![]() ·
· ![]()
2. Чему равно произведение квадратных корней?
– Произведение квадратных корней равно квадратному корню из произведения:
![]() ·
· ![]() =
= ![]()
3. Чему равен квадратный корень из дроби?
– Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя:
а > 0, b > 0, ![]()
![]() =
= ![]()
4. Чему равно частное квадратных корней?
– Частное квадратных корней равно квадратному корню из дроби:
![]() =
= ![]()
II. Восприятие и осознание нового материала
Работа с учебником.
№369, 370 – устно
С записью на доске и в тетрадях:
№373 (а,в);
№374 (вторая строка)
Как бы вы стали вычислять значение следующего выражения?
![]() – ?
– ?
Учащиеся предлагают два способа:
I способ: ![]()
![]() =
= ![]() =
= ![]() =7
=7
II способ: ![]() =
= ![]() =
= ![]() = 7
= 7
Какое решение более рациональное?
№ 377 (2 строка)
Формируют умения:
Л. - ясно, точно, грамотно излагать свои мысли в устной и письменной речи;
М. - работать по самостоятельному плану;
М. - использовать эталон для самопроверки;
П. - использовать математическую терминологию;
П. – применять теоремы о свойствах квадратных корней из произведения и дроби;
П. – применять формулы сокращенного умножения.
IV. Самостоятельная работа (работа в группах)
Поиграем «Вычисли и вставь слово вместо знака вопроса»
(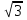 )²
)²
ПОДВАЛ ВАЛ
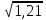 - 1,1
- 1,1
12 - 4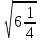
ПОЗВОНИТЬ ЗВОН
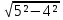
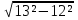
ПОСТУЛАТЫ ?
2,5 – 0,1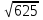
Формируют умения:
М. – организовать учебное взаимодействие в группе;
П. - использовать математическую терминологию;
П. – применять теоремы о свойствах квадратных корней из произведения и дроби
Резервное задание для обеспечения занятости и развития наиболее подготовленных учащихся.
![]()
Задание на смекалку: Используя 6 раз число ![]() и знаки действия, получить число 6.
и знаки действия, получить число 6.
Решение:
(![]() = 6
= 6
(3+![]() =6
=6
9 – 3 = 6
6 = 6
V. Домашнее задание
Выучить теоремы по теме «Квадратный корень из произведения и дроби»
Решить № 376(б,г,е); №372(б,г)
Творческое задание по карточкам:
Вычислив выражения и расставив их в порядке убывания значений, вы узнаете фамилию русского математика, основателя Петербургской математической школы.
Используя материалы Википедии, подготовить краткое сообщение о данном математике.
-
В
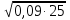
Е
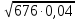
Б
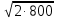
Е
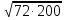
Ч
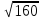 ∙
∙ 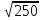
Ы
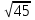 ∙
∙ 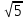
Ш
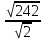
Формируют умения:
Л. – личную ответственность за будущий результат;
М. - умение слушать и слышать
М. - использовать эталон для самопроверки;
П. – применять теоремы о свойствах квадратных корней из произведения и дроби.
П. – применять формулы сокращенного умножения.
Рефлексия
Согласно словам Дистервега: «Не в количестве знаний заключается образование, но в полном понимании и искусном применении всего того, что знаешь», проведите самоанализ, ответив на вопросы на бланке. Как я знаю и применяю материал по теме: «Квадратный корень из произведения и дроби»:
а) на отлично;
б) хорошо;
в) удовлетворительно;
г) совсем не знаю и не могу применять.
Сегодня на уроке я поставил себе оценку …
| О себе | Об уроке | |
| Удовлетворен | ||
| Неудовлетворен |
Формируют умения:
Л. – понимать свои сильные и слабые стороны;
М. - оценивать степень своей индивидуальной деятельности.
Использованная литература:
-
Алгебра 8 : учебник для 8 кл. образоват. учреждений/ Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова – М.: Просвещение, 2013.
-
Журнал «Математика в школе»: - М. «Школьная пресса», 2001, №3 (стр. 36-39)
Здесь представлен конспект к уроку на тему «Квадратный корень из произведения и дроби», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

