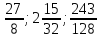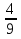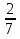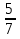Конспект урока «Прогрессии» по математике для 9 класса
Урок - зачет по теме: «Прогрессии» 9 класс.
Составила: Шемарова Татьяна Анатольевна, учитель математики МОУ «Средняя школа №16», г.Кимры.
Цель урока: повторить, обобщить, систематизировать изученный по главе материал; контроль приобретенных знаний.
Задачи урока:
Образовательные - повторить и обобщить изученный материал; закрепить формулы нахождения n -го члена арифметической и геометрической прогрессии; формулы нахождения суммы первых n членов арифметической и геометрической прогрессии; контроль и оценка знаний полученных в ходе изучения темы.
Развивающие - развитие логического и пространственного мышления учащихся; память; анализ.
Воспитательные - эстетическое воспитание; воспитание ответственности за конечный результат, самостоятельности.
Ход урока:
I. Устная работа:
1. дана арифметическая прогрессия 6,8,10,… найти следующие четыре члена прогрессии.
2. Дано 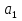 =2, d=3. Найти:
=2, d=3. Найти: 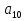 .
.
3. Найти разность арифметической прогрессии, если 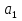 =7 и
=7 и 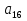 =67.
=67.
4. Найти сумму 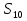 , если
, если 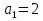 и
и 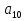 =20.
=20.
5. Арифметическая прогрессия задана формулой 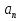 =3+4n. Найти
=3+4n. Найти 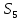 .
.
6. Зная первые два члена геометрической прогрессии 1,2,… найти следующие четыре.
7. В геометрической прогрессии 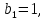 q=-2, найти
q=-2, найти 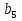 .
.
8) Найти сумму первых четырех членов геометрической прогрессии, в которой 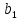 =3, q=2.
=3, q=2.
9) Геометрическая прогрессия задана формулой n члена 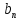 =2∙
=2∙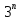 . Найти
. Найти 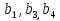 .
.
II. Зачет
Учащимся предлагаются 25 заданий в 2 вариантах. Ученики самостоятельно выбирают задания, которые могут решить. Перевод заработанных баллов в оценку дается перед началом урока.
На «3» - 5-8 баллов
«4» - 9-12 баллов
«5» - более 12 баллов.
Вопросы зачета:
1 вариант.
1. В арифметической прогрессии известно 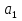 = -0,8 и d=4. Найти
= -0,8 и d=4. Найти 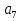 . (1 б.)
. (1 б.)
2. Зная первые два члена арифметической прогрессии 3; -2;… найти следующие за ними четыре её члена. (1б.)
3. Зная первые два члена геометрической прогрессии 3;12;…, найти следующие за ними четыре члена.(1б.)
4. Дана геометрическая прогрессия. Найти 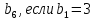 q=2. (1б.)
q=2. (1б.)
5. Последовательность -16; -13; … является арифметической прогрессией. Найдите сумму n первых её членов, если n=6. (2б.)
6. Найти сумму первых двенадцати членов арифметической прогрессии, в которой 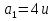 d =2. (2б.)
d =2. (2б.)
7. Найти сумму первых пяти членов последовательности, заданной формулой 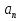 =3n+2. (2б.)
=3n+2. (2б.)
8. В геометрической прогрессии известно 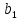 =1,6 и q=2. Найти
=1,6 и q=2. Найти 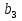 . (3б.)
. (3б.)
9. Найдите сумму пяти первых членов геометрической прогрессии, в которой 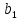 =32 и q=
=32 и q=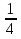 . (3б.)
. (3б.)
10. Найти сумму шести первых членов геометрической прогрессии 3,6, … (3б.)
11. Дана геометрическая прогрессия. Найти 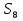
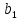 =10 и q=
=10 и q=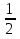 . (3б.)
. (3б.)
12. Найти разность арифметической прогрессии, если 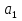 =4,
=4, 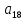 = -11. (3б.)
= -11. (3б.)
13. В арифметической прогрессии известно 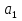 =14 и d=0,5. Найти номер члена прогрессии равного 19. (3б.)
=14 и d=0,5. Найти номер члена прогрессии равного 19. (3б.)
14. Мастерская изготовила в январе 106 изделий, а в каждый следующий месяц изготовляла на 12 изделий больше, чем в предыдущий. Сколько изделий изготовила мастерская в июне? (3б.)
15. Найдите первый член геометрической прогрессии, в которой 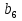 =
=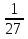 и q=
и q=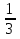 . (3б.)
. (3б.)
16. Найти сумму всех двухзначных чисел. (3б.)
17. Тело в первую секунду прошло 15 м, а в каждую следующую проходило на 2 м больше, чем в предыдущую. Какой путь прошло тело, за 26 сек.? (4б.)
18. Найдите знаменатель геометрической прогрессии, если известно, что 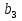 =12,
=12, 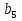 =48. (5б.)
=48. (5б.)
19. Найти сумму четырех первых членов геометрической прогрессии, в которой 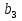 =
=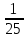 ,
, 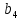 =
=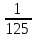 . (4б.)
. (4б.)
20. Является ли геометрической прогрессией последовательность (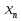 ), если
), если 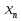 =2∙
=2∙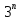 . (3б.)
. (3б.)
21. Найдите первый член геометрической прогрессии, в которой q=2, 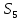 =93. (4б.)
=93. (4б.)
22. Найдите сумму первых восьми членов геометрической прогрессии, второй член которой равен 6, а четвертый равен 24. (4б.)
23. Найдите первый член и разность арифметической прогрессии, в которой 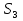 =48,
=48, 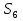 = -141. (5б.)
= -141. (5б.)
24. Докажите, что если последовательность (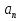 ) является арифметической прогрессией, то
) является арифметической прогрессией, то 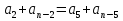 . (5б.)
. (5б.)
2 вариант.
1. В арифметической прогрессии известно 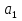 = -1,2 и d=3. Найти
= -1,2 и d=3. Найти 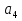 . (1б.)
. (1б.)
2. Зная первые два члена арифметической прогрессии 8; 4;… найти следующие за ними четыре её члена. (1б.)
3. Последовательность 4;-6;…, является арифметической прогрессией. Найдите сумму n первых её членов, если n =8. (1б.)
4. Зная первые два члена геометрической прогрессии 8; 6;…, найдите следующие за ним четыре члена прогрессии. (1б.)
5. Дана геометрическая прогрессия. Найти 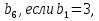 q=2. (2б.)
q=2. (2б.)
6. Найти сумму первых десяти членов арифметической прогрессии, в которой 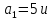 d =3. (2б.)
d =3. (2б.)
7. Найти сумму первых пяти членов последовательности, заданной формулой 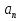 =4n+5. (2б.)
=4n+5. (2б.)
8. В геометрической прогрессии известно 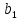 =3,2 и q=
=3,2 и q=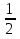 . Найти
. Найти 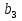 . (3б.)
. (3б.)
9. Найдите сумму шести первых членов геометрической прогрессии, в которой 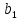 =27 и q=
=27 и q=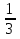 . (3б.)
. (3б.)
10. Найти сумму пяти первых членов геометрической прогрессии 8, 4, … (3б.)
11. Последовательность 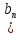 ) геометрическая прогрессия. Найти
) геометрическая прогрессия. Найти 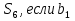 =2, q=3. (3б.)
=2, q=3. (3б.)
12. Найти разность арифметической прогрессии, если 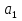 =5,
=5, 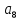 = 19. (3б.)
= 19. (3б.)
13. В арифметической прогрессии известно 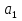 =-12 и d=3. Найти номер члена прогрессии равного 9. (3б.)
=-12 и d=3. Найти номер члена прогрессии равного 9. (3б.)
14. Бригада стеклодувов изготовила в январе 80 изделий, а в каждый следующий месяц изготовляла на 17 изделий больше, чем в предыдущий. Сколько изделий изготовила бригада в августе? (3б.)
15. Найдите первый член геометрической прогрессии, в которой 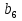 =
=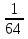 и q=
и q=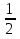 . (3б.)
. (3б.)
16. Найти сумму всех натуральных чисел, не превосходящих 50. (3б.)
17. Тело в первую секунду прошло 12 м, а в каждую следующую проходило на 3 м больше, чем в предыдущую. Какой путь прошло тело, за полчаса? (4б.)
18. Найдите знаменатель геометрической прогрессии, если известно, что 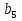 =11,
=11, 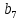 =99. (5б.)
=99. (5б.)
19. Найти сумму пяти первых членов геометрической прогрессии, в которой 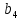 =
=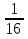 ,
, 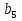 =
=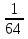 . (4б.)
. (4б.)
20. Является ли геометрической прогрессией последовательность (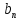 ), если
), если 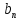 =
=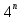 . (3б.)
. (3б.)
21. Найдите первый член геометрической прогрессии, в которой q=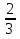 ,
, 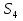 =65. (4б.)
=65. (4б.)
22. Найдите сумму первых шести членов геометрической прогрессии, третий член которой равен 54, а пятый равен 6. (4б.)
23. Найдите первый член и разность арифметической прогрессии, в которой 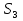 =60,
=60, 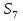 =59. (5б.)
=59. (5б.)
24. Докажите, что если последовательность (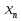 ) является арифметической прогрессией, то
) является арифметической прогрессией, то 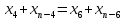 . (5б.)
. (5б.)
Ответы
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||||||||
| Ответ | 19,2 | -7; -12; -17; -22 | 48; 192; 768; 3072 | 96 | -51 | 180 | 55 | 6,4 | 42,625 | 189 | 16 | -1 | ||||||||||
| 1 вариант | ||||||||||||||||||||||
| № | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | |||||||||||
| Ответ | 11 | 166 | 9 | 4725 | 80 | 24 | 1 | Да | 3 | 765 |
d= -26 | | ||||||||||
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||||||||
| Ответ | 7,8 | 0; -4; -8; -12 | -240 |
| 96 | 162 | 85 | 0,5 | 121 | 15,5 | 728 | 2 | |||||||||
| 2 вариант | |||||||||||||||||||||
| № | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | | |||||||||
| Ответ | 8 | 199 | 0,5 | 1275 | 5409 | 55 | 5,3125 | Да | 27 | 728 |
d= 7 | | |||||||||
III. Домашнее задание: 16.55(в), 16.63, 17.47 (в), 17.52.
Литература
Дидактические материалы по алгебре для 9 кл/ Ю.Н. Макарычев, Н.Г. Миндюк и др.-М.: Просвещение, 2003.-160с., ил.
Алгебра. 9 класс. В 2 ч. Ч.2. Задачник для общеобразовательных учреждений/ А.Г. Мордкович, Л.А.Александрова и др. 12-е изд., исп. М. :Мнемозина, 2010 – 223с.: ил.
Здесь представлен конспект к уроку на тему «Прогрессии», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

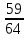
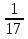
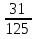
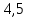 ;
;