Конспект урока «Лабораторная работа №3 Симплекс – метод решения задач. ПК №3» по информатике
Колледж АО «Финансовая академия»
Разработка открытого урока
Тема: «Лабораторная работа №3 Симплекс – метод решения задач. ПК №3»
Рассмотрен и одобрен на заседании
ЦК «Вычислительной техники и информационных систем»
Протокол № ___ от «__» _____ 201_г.
Председатель ЦК______ Стасишина Т.Г.
Преподаватель_______ Стасишина Т.Г.
Астана 2013г.
Тема: Лабораторная работа №3 Симплекс – метод решения задач. ПК №3
Дата: 27.02.2013г.
Группа 3ВТ-11-111
Цель:
Образовательная: Актуализация знаний о симплекс - методе и принципе его решения с помощью программы Microsoft Excel, умение применять полученные знания на практике, при выполнении заданий
Развивающая: Развивать наблюдательность, самостоятельность в решении учебных проблем, умения пользоваться приемами сравнения, обобщения, делать выводы, навыки работы с компьютерными программами, Развивать межпредметные связи
Воспитательная: Воспитывать у обучающихся последовательность и поэтапность действия, логику мышлений, деловой и творческий подход к работе, требовательность и самокритичность к себе, компьютерную грамотность, бережное отношение к оборудованию
Тип урока: комбинированный
Вид урока: закрепление и контроль знаний, умений, навыков
Средства обучения: программа Microsoft Excel, интерактивная доска
Технология обучения: интегрированный урок с применением интерактивных методов обучения.
Планируемые результаты:
В процессе освоения темы предлагается формирование следующих компетентностей у обучающихся:
-
получение и обработка информации;
-
использование различных критериев принятия решений (работа с итерациями);
-
принимать на себя ответственность за получаемое решение;
-
закреплять и применять межпредметные знания;
-
пользоваться приемами сравнения, обобщения, делать выводы;
-
самостоятельно пополнять и систематизировать свои знания.
Ход занятия
1. Орг. момент – приветствие, проверка присутствующих, указание темы, целей и задач занятия, ознакомить с ходом проведения занятия (3 минуты)
2. Опрос ранее пройденного материала (фронтальный опрос с использованием интерактивной доски) (10 минут)
Вопросы:
1. Дайте определение линейному программированию?
Линейное программирование (планирование) – метод отыскания максимума или минимума линейной функции при наличии ограничений в виде линейных неравенств или уравнений.
2. Что такое целевая функция?
Максимизируемая (минимизируемая) функции представляют собой принятый критерий эффективности решения задачи, соответствующей поставленной цели.
3. Дана задача. Составить к ней целевую функцию.
Для изготовления трёх видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цена каждого продукта приведены в таблице.
| Нормы расхода сырья на одно изделие | Запасы сырья | |||
| А | Б | В | | |
| I | 4 | 2 | 1 | 180 |
| II | 3 | 1 | 2 | 210 |
| III | 1 | 2 | 5 | 224 |
| Цена изделия | 10 | 14 | 12 | |
F(x)=10х1+14х2+12х3→мах
4. Что такое симплекс метод?
Симплекс – метод является алгебраической формой решения задачи линейного программирования.
5. Сколько этапов в решении задач симплекс – методом? Перечислите их.
Симплекс-метод реализуется в три этапа:
1 этап – запись задачи в таблицу;
2 этап – определение допустимого решения;
3 этап – определение оптимального решения.
6. Недостатки симплекс – метода.
Решение задач математического программирования при помощи симплекс-метода традиционными способами требует затрат большого количества времени.
7. Расскажите алгоритм решения задач симплекс – методом.
-
Поставленная описательная задача переводится в математическую форму (целевая функция и ограничения).
-
Полученное математическое описание приводят к канонической форме.
-
Каноническую форму приводят к матричному виду.
-
Ищут первое допустимое решение. Для этого матрица должна быть правильной. Матрица в ЗЛП называется правильной, если она содержит минимум m правильных (базисных) столбцов, где m – число строк в матрице. Столбец в канонической ЗЛП называется правильным (базисным), если все его элементы равны нулю, кроме единственного равного единице.
-
Если матрица не является правильной, то ее нужно сделать таковой с помощью искусственного базиса. Для этого в матрицу нужно дописать столько базисных столбцов, чтобы их общее количество вместе с уже имеющимися базисными столбцами составляло m. После этого переходят к пункту 6. Если искусственный столбец выходит из базиса, то его удаляют из матрицы. Если удалены все искусственные столбцы, то получено первое допустимое решение. Если искусственные элементы не удается вывести из базиса, то система не имеет решений.
-
Строят последовательность матриц. Нужно определить ведущий столбец, ведущую строку и ведущий элемент. Элемент, соответствующий ведущей строке, удаляется из базиса, а на его место ставят элемент, соответствующий ведущему столбцу. Составляют уравнение пересчета матрицы, выполняют пересчет, а затем проверяют его результаты на оптимальность. Если решение не оптимально, то заново ограничивают ведущий элемент, ведущую строку и ведущий столбец.
8. Что такое разрешающий столбец, разрешающая строка, разрешающий элемент, итерация?
Разрешающим столбцом является тот в котором находится наибольший положительный элемент индексной строки при отыскании Fmin или наименьший отрицательный элемент при отыскании Fmax.
Разрешающей строкой называется та, в которой содержится наименьшее положительное частное от деления элементов столбца на соответствующие элементы ключевого столбца.
На пересечении строки и столбца находится разрешающий элемент.
9. Дана итерация. Укажите разрешающей столбец, разрешающую строку, разрешающую ячейку
Итерация О
| B | x1 | x2 | x3 | x4 | x5 | x6 | |
| x4 | 10 | 0 | 2 | 3 | 1 | 0 | 0 |
| x5 | 4 | 1 | -2 | 1 | 0 | 1 | 0 |
| x6 | 11 | 3 | 2 | 1 | 0 | 0 | 1 |
| F(X0) | 0 | 0 | -2 | -3 | 0 | 0 | 0 |
Как будет записана итерация 1?
Итерация 1
| B | x1 | x2 | x3 | x4 | x5 | x6 | |
| x3 | 31/3 | 0 | 2/3 | 1 | 1/3 | 0 | 0 |
| x5 | 2/3 | 1 | -22/3 | 0 | -1/3 | 1 | 0 |
| x6 | 72/3 | 3 | 11/3 | 0 | -1/3 | 0 | 1 |
| F(X1) | 10 | 0 | 0 | 0 | 1 | 0 | 0 |
3. Выполнение задания лабораторной работы – контроль и оказание помощи (35 минут)
3.1 Решение задач
Лабораторная работа №3
Цель: расчет задач линейного программирования с помощью симплекс метода
Содержание работы
-
Ознакомиться с решенным примером задачи линейного программирования с помощью симплекс метода.
-
Воспроизвести задачу в электронном виде, используя программу Microsoft Excel.
-
Работа с тестирующей программой MyTest.
-
Составить отчет по работе.
Задача об использовании ресурсов (задача планирования производства).
Для изготовления двух видов продукции Р1 и Р2 используют четыре вида ресурсов S1,S2,S3 и S4.Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1.
| запас ресурсов | Число единиц ресурсов, затрачиваемых на изготовление единицы продукции | ||
| P1 | P2 | ||
| S1 | 18 | 1 | 3 |
| S2 | 16 | 2 | 1 |
| S3 | 5 | - | 1 |
| S4 | 21 | 3 | - |
Прибыль, получаемая от единицы продукции P1 и P2 – соответственно 2 и 3 тенге.
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
РЕШЕНИЕ: Составим экономико–математическую модель задачи.
Обозначим х1 и х2 – число единиц продукции соответственно P1 и P2, запланированных к производству. Для их изготовления (1*Х1 + 3*Х2) единиц ресурса S1, (2*Х1+1*Х2) единиц ресурса S2, (1*Х2) единиц ресурса S3 и 3Х1 единиц ресурса S4. Так как потребление ресурсов S1, S2, S3, S4 не должны превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потребителями ресурсов и их запасами выразится системой неравенств:
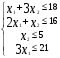
По смыслу задачи переменные
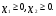
Суммарная прибыль составит 2Х1 тенге от реализации продукции P1 и 3Х2 тенге – от реализации продукции P2 , т.е.
F= 2Х1 +3Х2
Приведем к каноническому виду, добавив дополнительные переменные к левым частям ограничений. Получим
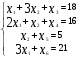
F- 2Х1 -3Х2=0
Заполняем первую симплекс-таблицу в которой переменные Х3, Х4, Х5, Х6 основные. Последняя строка заполняется коэффициентами линейной функции с противоположным знаком.
| решение | Переменные | Оценочные отношения | ||||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | | ||
| Х3 | 18 | 1 | 3 | 1 | 0 | 0 | 0 | 18/3 |
| Х4 | 16 | 2 | 1 | 0 | 1 | 0 | 0 | 16 |
| Х5 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5 |
| Х6 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | |
| F | 0 | -2 | -3 | 0 | 0 | 0 | 0 | |
Проверим критерий оптимальности, в строке имеются отрицательные элементы. Выбираем из них наибольший по модулю (-3). Второй столбец разрешающий, переменная Х2 в основные. Затем находим оценочные отношения и Х2=min {18/3;16;5; бесконечность}=5 Третья строка является разрешающих строки и столбца стоит разрешающий элемент а33= 1.Строим новую таблицу по правилам симплекс метода:
а) в новом базисе основные переменные:х3,х4,х5,х6;
б) расставляем нули и единицы; В последней строке против всех переменных ставим 0.Третья строка получается делением на разрешающий элемент а33= 1. Остальные клетки заполняются по правилу прямоугольника
| решение | Переменные | Оценочные отношения | ||||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | | ||
| Х3 | 3 | 1 | 0 | 1 | 0 | -3 | 0 | 3 |
| Х4 | 11 | 2 | 0 | 0 | 1 | -1 | 0 | 11/2 |
| Х5 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | |
| Х6 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | 7 |
| F | 15 | -2 | 0 | 0 | 0 | 3 | 0 | |
Критерий оптимальности вновь не выполнен . Теперь первый столбец разрешающий; Х1 – переходит в основные, min {3/1;11/2;,;7 }=3; первая строка разрешающая, а11 – разрешающий элемент.
Новая симплекс таблица примет вид:
| решения | Переменные | Оценочные отношения | ||||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | | ||
| Х3 | 3 | 1 | 0 | 1 | 0 | -3 | 0 | бесконечность |
| Х4 | 5 | 0 | 0 | -2 | 1 | 5 | 0 | 5/5 |
| Х5 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5/1 |
| Х6 | 12 | 0 | 0 | -3 | 0 | 9 | 1 | 12/9 |
| F | 21 | 0 | 0 | 2 | 0 | -3 | 0 | |
И на этот раз критерий оптимальности не выполнен. Теперь пятый столбец и пятая строка разрешающие, а 25 = 5 – разрешающий элемент.
Переходим к следующей таблице.
| Решения | Переменные | Оценочные отношения | ||||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | | ||
| Х3 | 6 | 1 | 0 | 1/5 | /5 | 0 | 0 | |
| Х4 | 1 | 0 | 0 | 2/5 | 1/5 | 1 | 0 | |
| Х5 | 4 | 0 | 1 | 2/5 | -1/5 | 0 | 0 | |
| Х6 | 3 | 0 | 0 | /5 | -9/5 | 0 | 1 | |
| F | 24 | 0 | 0 | 4/5 | 3/5 | 0 | 0 | |
Критерий оптимальности выполнен, значит F max = 24 Оптимальное базисное решение (6;4;0;0;1;3)
Дополнительное задание.
Кожгалантерейное предприятие в планируемом периоде располагает тремя видами сырья (кожа, замша и кожезаменители) соответственно в количествах 60 кв.м, 75 кв.м, 50 кв.м, из которого производится продукция трех видов костюмы, куртки, плащи. Расход сырья на единицу продукции каждого вида приведен в таблице:
Таблица 1.
| Ограничения на сырье | Нормы расхода сырья на единицу продукции | |||
| Костюмы | Куртки | Плащи | ||
| Кожа | 60 | 4 | 2 | 2 |
| Замша | 75 | 3 | 1 | 2 |
| Кожезаменители | 50 | 1 | 3 | 3 |
| Прибыль за тыс.тенге/ед.. | -- | 24 | 16 | 10 |
Найти такой план выпуска изделий, при котором предприятие получит максимальную прибыль, если известно, что прибыль от реализации единицы продукции костюмов составит 24 тыс. тенге/ед., курток - 16 тыс. тенге/ ед., а от продажи плащей - 10 тыс. тенге/ед.
Содержание отчета.
-
Сохранить решение задачи в своей папке.
-
Объясните технологию записи критерия оптимальности.
-
Указать формулы, по которым производится расчет.
-
Как определяется количество итераций для задачи?
-
По каким параметрам устанавливаются базисные переменные?
Задание 3.2. Работа с тестирующей программой MyTest
Вопросы.
-
В каком году впервые был разработан и применен симплекс-метод
- 1946
+ 1947
- 1948
- 1949
- 1950
2. Кто является разработчиком симплекс-метода?
- Блез Паскаль
- Джон фон Нейман
- Гаспар Монж
- Леонид Канторович
+ Джордж Данциг
3. Что такое итерация?
- Разрешающий элемент
- Разрешающая строка
- Разрешающий столбец
+ Симплекс-таблица
- Канонический вид
4. В основу симплексного метода положена идея
- получения канонического вида
- работы с системами уравнений
+ последовательного улучшения получаемого решения
- использования ограничений
- массового обслуживания
5. Сколько этапов решения задач симплекс методом?
- 2
+ 3
- 4
- 5
-6
6. Перечислите этапы решения задач симплекс – методом
+ запись задачи в таблицу, определение допустимого решения, определение оптимального решения
- запись задачи в таблицу, разработка итераций, определение оптимального решения
- нахождения ограничений, перевод функций к каноническому виду, определение допустимого решения
- установка ограничений к задаче, изменение формы представления данных, определение способов решения
- перевод табличной формы к каноническому виду, разработка итераций, определение способов решения
7. При отыскании Fmin разрешающим столбцом будет являться тот в котором
- находится базовое значение индексной строки
- находится единичная матрица индексной строки
- находится нулевой элемент индексной строки
- находится наименьший отрицательный элемент индексной строки
+ находится наибольший положительный элемент индексной строки
8. При отыскании Fmах разрешающим столбцом будет являться тот в котором
- находится базовое значение индексной строки
- находится единичная матрица индексной строки
- находится нулевой элемент индексной строки
+ находится наименьший отрицательный элемент индексной строки
- находится наибольший положительный элемент индексной строки
9. В приведенной таблице разрешающий столбец
| B | x1 | x2 | x3 | x4 | x5 | x6 | |
| x4 | 10 | 0 | 2 | 3 | 1 | 0 | 0 |
| x5 | 4 | 1 | -2 | 1 | 0 | 1 | 0 |
| x6 | 11 | 3 | 2 | 1 | 0 | 0 | 1 |
| F(X0) | 0 | 0 | -2 | -3 | 0 | 0 | 0 |
- х1
- х2
+ х3
-х4
-х5
10. Выражение, которое необходимо максимизировать называется:
+ целевой функцией
- разрешающим элементом
- канонической формой
- допустимым неравенством
- итерацией
11. Для изготовления 4-ёх видов продукции P1, P2, P3, P4 используют два вида сырья: S1 и S2 . Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а так же величина прибыли, получаемая от реализации единицы продукции, приведены в таблице.
| Запас сырья | Количество единиц сырья, идущих на изготовление единицы продукции | ||||
| P1 | P2 | P3 | P4 | ||
| S1 | 5 | 1 | 6 | 3 | 6 |
| S2 | 4 | 1 | 1 | 1 | 4 |
| Прибыль от единицы продукции | 5 | 10 | 9 | 28 | |
Как запишется целевая функция к задаче?
- 5х1+10х2+9х3+28х→min
+ 5х1+10х2+9х3+28х→max
- х1+6x2+3x4+6x4→min
- x1+x2+x3+4x4→min
- 5x1+4x2→max
12. При перемещении или копировании в электронной таблице относительные ссылки:
- не изменяются
- преобразуются вне зависимости от нового положения формулы
+ преобразуются в зависимости от нового положения формулы
- преобразуются в зависимости от длины формулы
- удаляются автоматически
13. При перемещении или копировании в электронной таблице абсолютные ссылки:
+ не изменяются
- преобразуются вне зависимости от нового положения формулы
- преобразуются в зависимости от нового положения формулы
- преобразуются в зависимости от длины формулы
- удаляются автоматически
14. Надстройка Excel, которая позволяет решать оптимизационные задачи
- Мастер подстановок
+ Поиск Решения
- Пакет анализа
- Мастер суммирования
- Автозаполнение
15. Метод отыскания максимума или минимума линейной функции при наличии ограничений в виде линейных неравенств или уравнений называется:
- Линейное моделирование
- Линейная форма
- Линейная итерация
+ Линейное планирование
- Линейная область
4. Промежуточный контроль №3 (25 минут)
«Удовлетворительно» - решить задачу с помощью надстройки «Поиск решения»
«Хорошо» - решить задачу с помощью симплекс – метода
«Отлично» - решить задачу с помощью симплекс – метода и надстройки «Поиск решения»
Вариант 1
Для изготовления четырёх видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.
| Нормы расхода сырья на одно изделие | Запасы сырья | ||||
| А | Б | В | Г | | |
| I II III | 1 1 1 | 2 1 3 | 1 2 3 | 0 1 2 | 18 30 40 |
| Цена изделия | 12 | 7 | 18 | 10 | |
-
Как изменяется общая стоимость продукции и план её выпуска при увеличении запасов сырья I и II вида на 4 и 3 ед. соответственно и уменьшении на 3 ед. сырья III вида?
-
Целесообразно ли включать в план изделие Д ценой 10 ед., на изготовление которого расходуется по 2 ед. каждого вида сырья?
Вариант 2
Для изготовления четырёх видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цена каждого продукта приведены в таблице.
| Нормы расхода сырья на одно изделие | Запасы сырья | ||||
| А | Б | В | Г | | |
| I II III | 1 0 4 | 0 1 2 | 2 3 0 | 1 2 4 | 180 210 800 |
| Цена изделия | 9 | 6 | 4 | 7 | |
-
Как изменяется общая стоимость продукции и план её выпуска при увеличении запасов сырья I и II вида на 120 и 160 ед. соответственно и одновременном уменьшении на 60 ед. запасов сырья I вида?
-
Целесообразно ли включать в план изделие Д ценой 12 ед., на изготовление которого расходуется по 2 ед. каждого вида сырья?
Вариант 3
Для изготовления трёх видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цена каждого продукта приведены в таблице.
| Нормы расхода сырья на одно изделие | Запасы сырья | |||
| А | Б | В | ||
| I II III | 4 3 1 | 2 1 2 | 1 2 5 | 180 210 244 |
| Цена изделия | 10 | 14 | 12 | |
-
Как изменится общая стоимость продукции и план её выпуска при увеличении запасов сырья I и II вида на 4 ед. каждого?
-
Целесообразно ли включать в план изделие Г ценой 13 ед., на изготовление которого расходуется соответственно 1, 3 и 2 ед. каждого вида сырья, и изделие Д ценой 12 ед., ни изготовление которого расходуется по 2 ед. каждого сырья?
Вариант 4
Для изготовления четырёх видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цена каждого продукта приведены в таблице.
| Нормы расхода сырья на одно изделие | Запасы сырья | ||||
| А | Б | В | Г | | |
| I II III | 2 1 2 | 1 2 4 | 3 4 1 | 2 8 1 | 200 160 170 |
| Цена изделия | 5 | 7 | 3 | 8 | |
-
Как изменяется общая стоимость продукции и план её выпуска при увеличении запасов сырья I и II вида на 8 и 10 ед. соответственно одновременном уменьшении на 5 ед. запасов сырья III вида?
-
Целесообразно ли включать в план изделие Д ценой 10 ед., на изготовление которого расходуется по 2 ед. каждого вида сырья?
5. Подведение итогов занятия (5 минут).
Выставление полученных оценок за урок в журнал.
6. Домашнее задание
Т.Л. Партыка, И.И. Попов «Математические методы», стр. 89-94, М. Форум – Инфра-М, 2009г.
Решить задачу (пункт а, б):
Предприятие выпускает два вида продукции А и В, для производства которых используется сырье трех видов. На изготовление единицы изделия А требуется затратить сырья каждого вида а1 , а2 , а3 кг соответственно, а для единицы изделия В – b1 , b2 , b3 . Производство обеспечено сырьем каждого вида в количестве P1, P2, P3 . Стоимость единицы изделия А составляет α тенге., а единицы изделия В – β тенге. Требуется составить план производства изделий А и В, обеспечивающий максимальную стоимость готовой продукции.
а) Составить экономико-математическую модель задачи,
б) Решите задачу симплекс-методом,
в) Сформулируйте двойственную задачу и найдите ее решение,
г) Решите исходную задачу графически.
| а2 | а3 | b1 | b2 | b3 | P1 | P2 | P3 | α | β | |
| 4 | 2 | 1 | 1 | 3 | 5 | 240 | 180 | 251 | 40 | 30 |
Резервное задание
Предприятие рекламирует свою продукцию с использованием четырех источников массовой информации: телевидения, радио, газет и расклейки объявлений. Анализ рекламной деятельности в прошлом показал, что эти средства массовой информации приводят к увеличению прибыли соответственно на 10,5,7и 4 у.е. в расчете на 1 у.е. затраченную на рекламу. На рекламу выделено 50000 у.е. Администрация предприятия не намерена тратить на телевидение более 40%, а на радио и газеты – более 50% от общей суммы выделенных средств. Как следует предприятию организовать рекламу, чтобы получить максимальную прибыль?
Решение:
Составим математическую модель задачи.
Цель – максимизация прибыли.
Параметрами являются все числа, приведенные в условии задачи.
Управляющие переменные:
Х1 – количество средств, вложенных в рекламу на телевидение;
Х2 – количество средств, вложенных в рекламу на радио;
Х 3- количество средств, вложенных в рекламу в газетах;
Х4 - количество средств, вложенных в рекламу, организованную с помощью расклейки объявлений.
Область допустимых решений имеет вид:
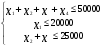
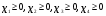
Она содержит ограничения по общей сумме выделенных средств, по количеству средств, предусмотренных на рекламу по телевидению, на радио и газетах, и условия не отрицательности управляющих переменных.
Критерий оптимальности записывается следующим образом:
P= 10х1+5х2+7х3+4х4max
Здесь представлен конспект к уроку на тему «Лабораторная работа №3 Симплекс – метод решения задач. ПК №3», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Информатика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

