Презентация "Система счисления" (6 класс) по математике – проект, доклад
Презентацию на тему "Система счисления" (6 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Система счисления. Происхождение числа ноль
ЦЕЛЬ ИССЛЕДОВАНИЯ. Исследование причин отсутствия числа ноль в системах счисления древних цивилизаций. ЗАДАЧИ ИССЛЕДОВАНИЯ. Узнать ,какие были системы ...Древнеславянская система счисления
Единицы, десятки и сотни. Большинство букв древнерусского алфавита имели числовое соответствие Буква «Аз» означала «один», «,веди» — «два» Некоторые ...Десятичная система счисления
Числа, которые могут быть получены в результате счета предметов-1,2,3,45 и т.д., называют натуральными. Числа 1,2,3,4,5,6,7,8,9, 0 называют арабскими. ...Двоичная система счисления
Вильгельм Готфрид Лейбниц (1646-1716). Медаль, нарисованная В. Лейбницем в 1697 г., поясняющая соотношение между двоичной и десятичной системами исчисления. ...Двоичная система счисления
Системы счисления. Системы счисления – это определенные правила записи чисел и связанные с этими правилами способы выполнения вычислений. Позиционная ...Двоичная система счисления
Повторим тему «Системы счисления». Основные понятия систем счисления. Система счисления. - это способ записи чисел и связанные с ними способы выполнения ...Арифметические операции в позиционных системах счисления
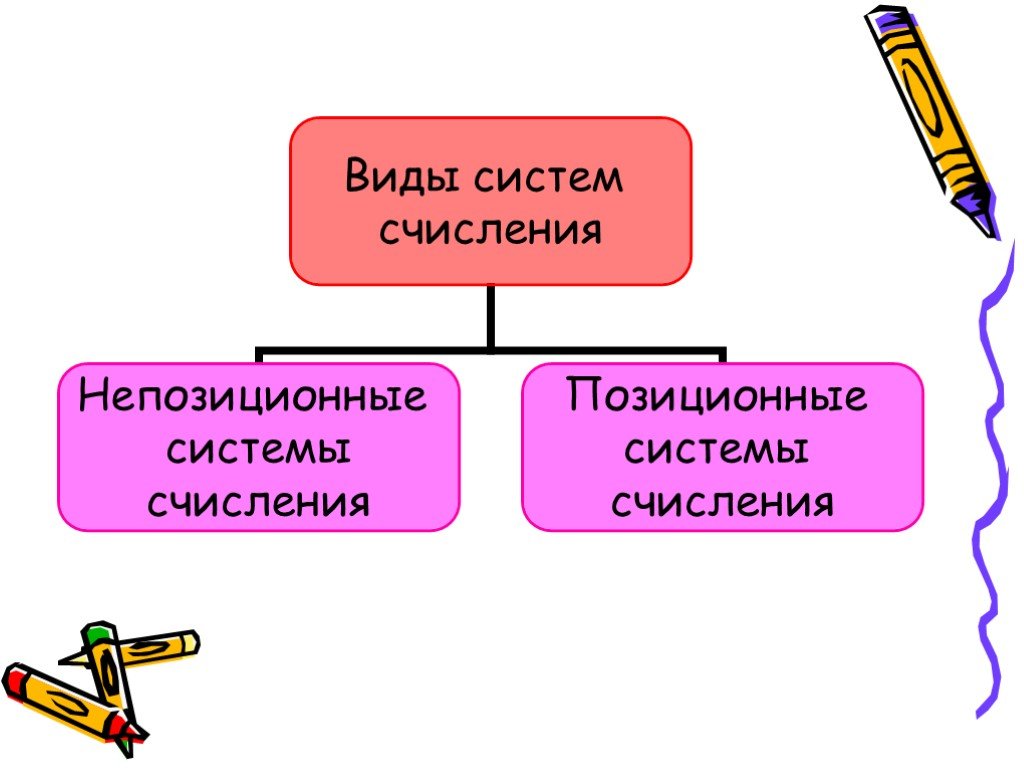
Ответьте на вопросы:. Какие системы называются НЕПОЗИЦИОННЫМИ? Какие системы называются ПОЗИЦИОННЫМИ? Какое число называют – ОСНОВАНИЕ позиционной ...Перевод чисел в позиционных системах счисления
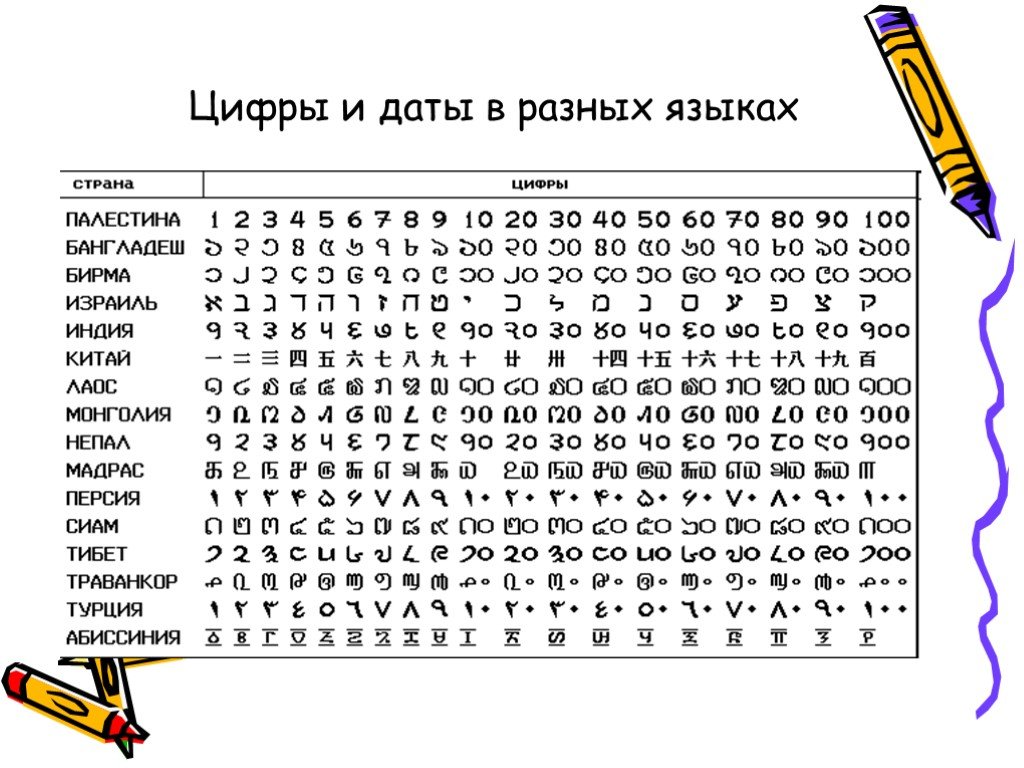
Проверка домашнего задания. 1210=11002 52310=10000010112 7610=10011002 12110=11110012. 85610=15308 11110=1578 9810=1428 12610=1768. 90710=38B16 65910=29316 ...Числа в различных системах счисления
«Нет такой нелепости,которую бы не изрекли философы.» Цицерон. 2 * 2 = 4 ? - Это очевидно ! - Не всегда очевидное является истиной. Я утверждаю, что ...Римская система счисления
Цель работы:. Познакомиться с историей возникновения и развития римской системы счисления Познакомиться с правилами составления чисел римской системы ...Система компьютерной алгебры GAP
Как расшифровать “GAP” ? Groups Algorithms Programming. Что такое GAP ? Компьютерная алгебра – современная область науки, возникшая на стыке математики ...История систем счисления
Десятичная система счисления. Обычная система записи чисел который мы привыкли пользоваться жизни. Десятичная система счисления встречается везде ...Системы счисления
Система исчисления. Система счисления это совокупность цифровых знаков и правил их записи, применяемая для однозначной записи чисел. Непозиционной ...Система старинных мер в современном обществе
Цель работы: рассмотрение практического применения старинных мер измерения на современном этапе развития общества. Задачи: Изучить причины и предпосылки ...Система работы по подготовке учащихся 11 класса к ЕГЭ
ЕГЭ по математике является обязательным и по праву считается одним из самых сложных. Сложность этого экзамена вызвана как распространенной "нелюбовью" ...Система линейных уравнений с двумя переменными
Рассмотрим систему двух линейных уравнений с двумя переменными х – 2у = 1, х - у = - 1. Что называют решением системы уравнений? Является ли пара ...Система координат в пространстве
Вспомним, как определяется координатная(числовая) прямая. Изображаем произвольную прямую;. х 0 1 М а. Тогда любой точке этой координатной прямой соответствует ...Перевод чисел в десятичную систему счисления
Представление чисел в развернутой форме. 34510=5*100+4*101+3*102 10,112=0*20+1*21+1*1/2+1*1/4 67,58=7*80+6*81+5*8-1+8*8-2. Перевод числа из двоичной ...Перевод целых чисел из десятичной системы счисленияв другие системы счисления
Сколько лет каждому из вас в 8-ричной или 16-ричной системах счисления? «10», «11», «100», «101» - такой была бы шкала оценок в школе в двоичной системе ...Перевод целых чисел в 2, 8, 16-ую системы счисления
8 10 16. Возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления ...Конспекты
Понятие о системах счисления
Етова Юлия Вячеславовна. Учитель информатики. ГБОУ Центр Образования №1469, город Москва. Понятие о системах счисления. ...Двоичная система счисления
УРОК. На тему. «Двоичная система счисления». . . в 9 классе. . ШОРИН П.М. Тема урока. : Разработка теста в табличном ...Системы счисления
Описательная часть конспекта урока. Тема:. Системы счисления. . . Учитель:. Лескова С.Г. . Цель занятия:. . . . учащиеся формируют ...Системы счисления
Бородина Татьяна Анатольевна. ,. учитель информатики . ГБОУ СОШ № 3 г. Сызрани. . Тема урока:. . Системы счисления. Цель урока:. . закрепить, ...Системы счисления
Конспект урока:. «Системы счисления». Вид урока:. урок систематизации и обобщения изученного материала, урок-игра. Формы работы. ...Система уравнений с двумя переменными
Тема: «Система уравнений с двумя переменными». Цели урока:. -Систематизировать , обобщить и закрепить знания по теме. -Научиться определять ...Система нелинейных уравнений с двумя переменными
ГУ «Средняя школа №115 отдела образования акимата города Костаная». Конспект урока по алгебре. в 9 классе. «Система ...Система нелинейных неравенств с двумя переменными
Зарипова Гульфира Абдулгаязовна, учитель математики, КГУ «СОШ № 31», г. Семей, ВКО эл. адрес:. zaripova. -. gulfira. @. mail. . ru. . . Разработка ...Система двух уравнений с двумя неизвестными
Конспект урока для 7 класса на тему. «. Система двух уравнений с двумя неизвестными». Разработано: учителем математики. МОУ «СОШ» п. Аджером. ...Название мерок в десятичной системе счисления
Гимназия имени Ф.К. Салманова, город Сургут. Конспект урока по математике. 2 класс. Учитель начальных классов. Мулюкова Рената Илдусовна. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 ноября 2018
Категория:Математика
Классы:
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию