Презентация "Доказательство теоремы Пифагора" по математике – проект, доклад
Презентацию на тему "Доказательство теоремы Пифагора" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
Тайны теоремы Пифагора
Задачи. 1. Собрать материал о истории открытия теоремы. 2. Взять интервью у учителя истории. 3. Узнать кто доказал теорему. 4. Выяснить заслугу древнегреческих ...Cпособы доказательства теоремы Пифагора
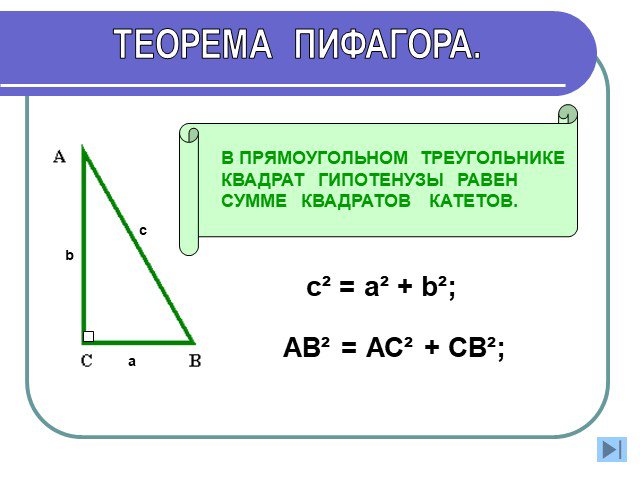
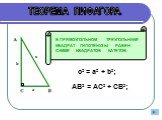
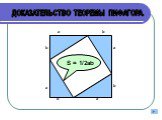
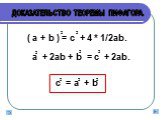
a2+b2=c2 c a b П. Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым ...Решение теоремы Пифагора
Биография Пифагора. Письменных документов о Пифагоре Самосском не осталось, а по более поздним свидетельствам трудно восстановить подлинную картину ...Теорема Пифагора доказательство
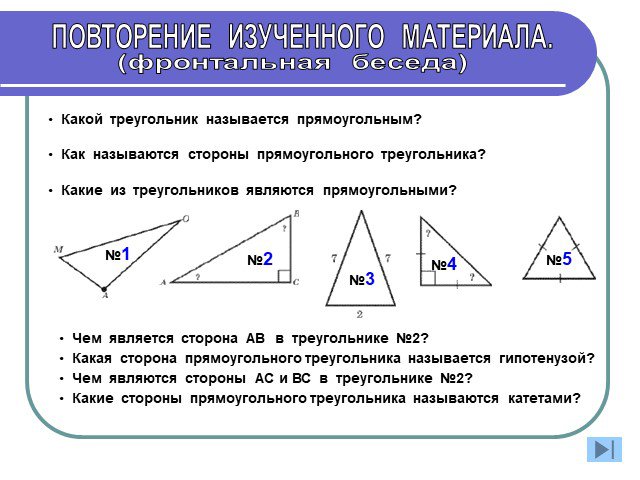
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. Елекова Э.М. Республика Алтай. Смотри и докажи! (∆ АВС- прямоугольный ...Различные доказательства теоремы Пифагора
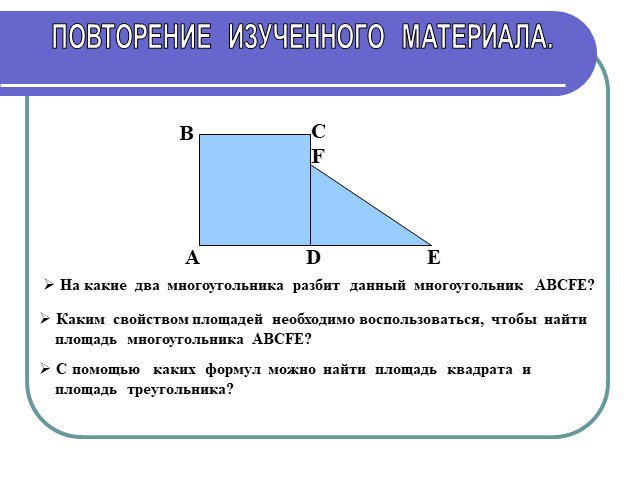
Теорема Пифагора. Структура задачи Дано. Что нужно доказать. Доказательство. CAB–прямоугольный треугольник. A B c Дано:. Доказать: SBAED=SFGAC+SHCBI. ...Различные подходы к доказательству теоремы Пифагора
На протяжении веков были даны многочисленные разные доказательства теоремы Пифагора... Чертеж к теореме Пифагора в средневековой арабской рукописи. ...Применение теоремы Пифагора в строительстве
Актуальность данного исследования. существует около 500 различных доказательств этой теорем (геометрических, алгебраических, механических), которые ...Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач
Объект исследования: Теорема Пифагора и пифагоровы тройки. Предмет исследования: Применение пифагоровых троек для быстрого решения геометрических ...История теоремы Пифагора
Цель нашего исследования. Мы хотим узнать, можно ли доказать теорему Пифагора другими способами (не так, как в учебнике)? Гипотеза Мы считаем, что ...История теоремы Пифагора
История теоремы Пифагора. Хронология развития теоремы до Пифагора:. Исторический обзор начнём с древнего Китая. Здесь особое внимание привлекает математическая ...История теоремы Пифагора
Цели: 1.Расширить свои знания по истории математики. 2.Узнать больше информации, легенд, мифов о Пифагоре и его теореме. 3.Ознакомиться с другими ...История открытия теоремы Пифагора
Введение. Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался ...Некоторые применения теоремы Пифагора
Ниже будем использовать следующие обозначения: катеты и гипотенуза прямоугольного треугольника ABC соответственно a, b и c ; sin A = a / c, sin B ...По следам теоремы Пифагора
« Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, которую можно сравнить с мерой золота…» И. Кеплер. Цель: внимательно ...Многообразие методов доказательства теоремы Пифагора
Теорема Пифагора. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Исторические сведения. Пифагор – древнегреческий ученый ...Док-ва Теоремы Пифагора
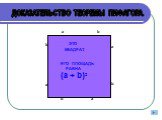
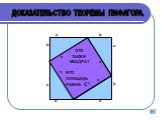
Доказательства. Пусть ABC — данный прямоугольный с треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С (рис. 6). По определению ...Интересные факты о теореме Пифагора
Теорема Пифагора - одна из основопологающих теорем в геометрии,также является одной из известнейших теорем. Формулировка: Формула:. В прямоугольном ...Теорема Пифагора
ОБЛАСТИ ПРИМЕНЕНИЯ. Строительство Астрономия Мобильная связь. Мобильная связь. Какую наибольшую высоту должна иметь антенна мобильного оператора, ...Теорема Пифагора
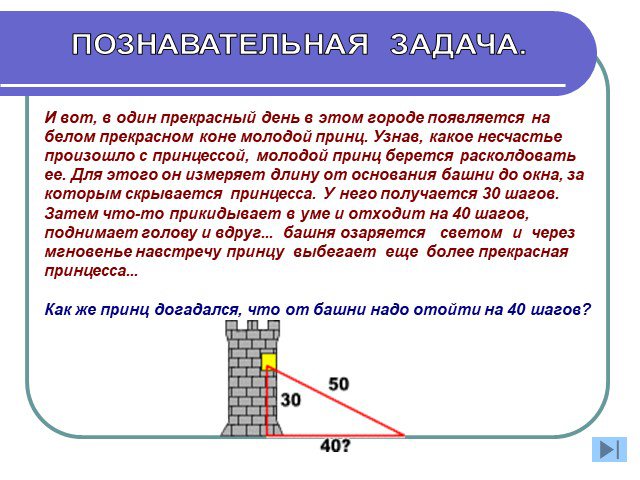
Задача 1. Лестница длиной 12,5 м приставлена к стене так, что расстояние нижнего конца лестницы от стены равно 3,5 м. На какой высоте от земли упирается ...Теорема Пифагора
Биография Пифагора. Великий ученый Пифагор родился около 570г. до н. э. на острове Самос. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. ...Конспекты
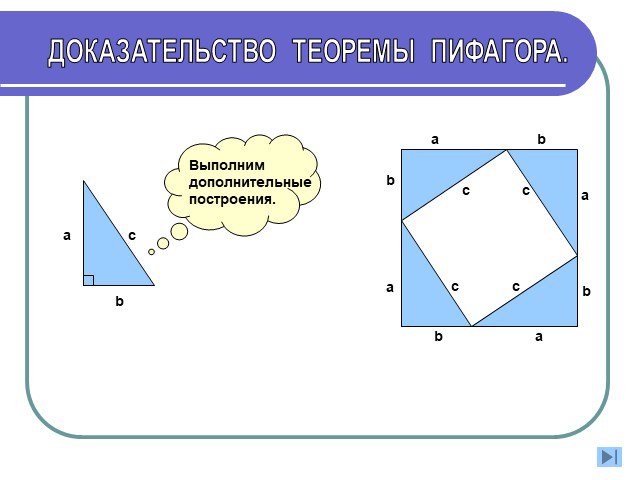
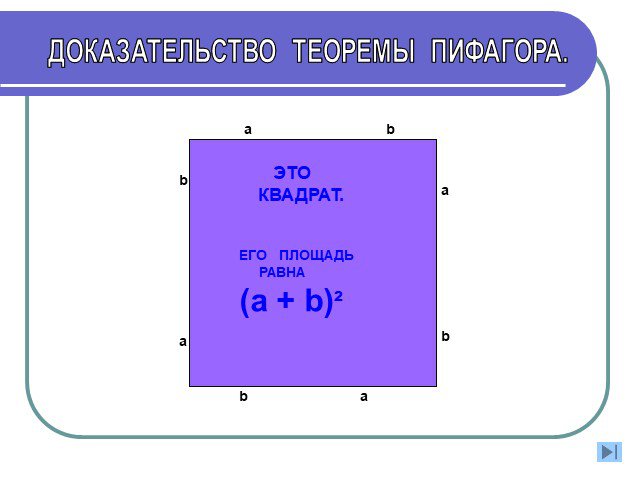
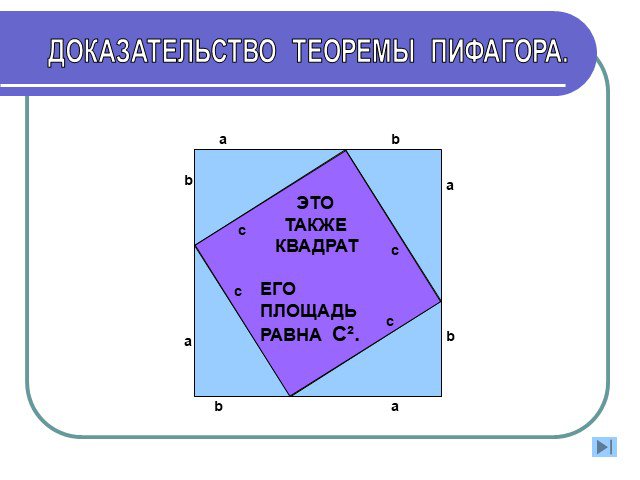
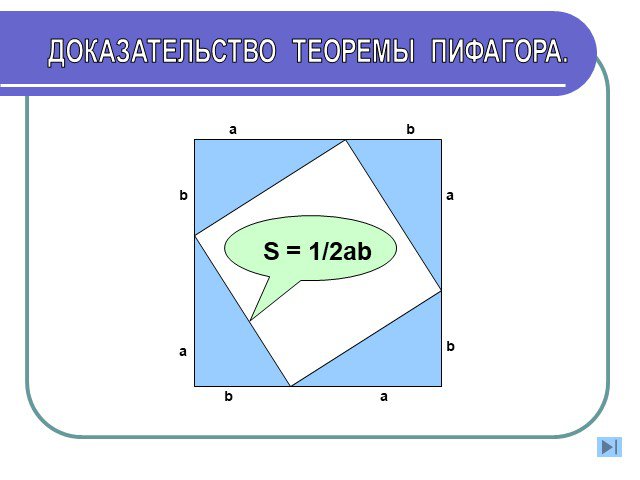
Доказательство теоремы Пифагора
Министерство образования и науки Российской Федерации. Управление образования администрации города Твери. МОУ Тверская гимназия № 10. Региональный ...Решение задач с помощью теоремы Пифагора
Использование кейс - технологий на уроках математики. Урок геометрии в 8 классе. Тема урока: Решение задач с помощью теоремы Пифагора. Цели ...Различные способы доказательства теоремы Пифагора
Ход урока:. . Здравствуйте, садитесь. Меня зовут Людмила Александровна, я рада всех Вас видеть (слайд 1). Пребудет вечной истина, как скоро. ...Теорема Пифагора
План – конспект урока геометрии в 8 классе. по теме «Теорема Пифагора». Учитель: Платонова Валентина Николаевна. Цель урока. : изучить доказательство ...Теорема Пифагора
VII ВСЕРОССИЙСКИЙ КОНКУРС. ПРОФЕССИОНАЛЬНОГО МАСТЕРСТВА ПЕДАГОГОВ. «МОЙ ЛУЧШИЙ УРОК». естественно-научное направление. Муниципальное ...Теорема Пифагора
Тема урока по геометрии в 8-м классе: "Теорема Пифагора». Цели урока:. Образовательная:. обеспечить понимание доказательства теоремы Пифагора ...Теорема Пифагора
Тема урока:. Теорема Пифагора. Цели урока:. Образовательные: сформулировать и доказать теорему Пифагора,. . рассмотреть основные следствия из ...Изучая теорему Пифагора, изучаем её историю
Конференция по геометрии. по теме. «Изучая теорему Пифагора, изучаем её историю». Цели:. · Воспитание устойчивого интереса к изучению предмета ...Теорема Пифагора
Урок по геометрии по теме: «Теорема. Пифагора». Подготовила: Сеитова Лариса Ромазановна, учитель математики муниципального казённого общеобразовательного ...Теорема Пифагора
Тема: Теорема Пифагора. «Кто смолоду делает, думает сам. тот становится потом надежнее. крепче, умнее ». В. Шукшин. Цель обучения :. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Волокова Т.В., учитель математики
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию