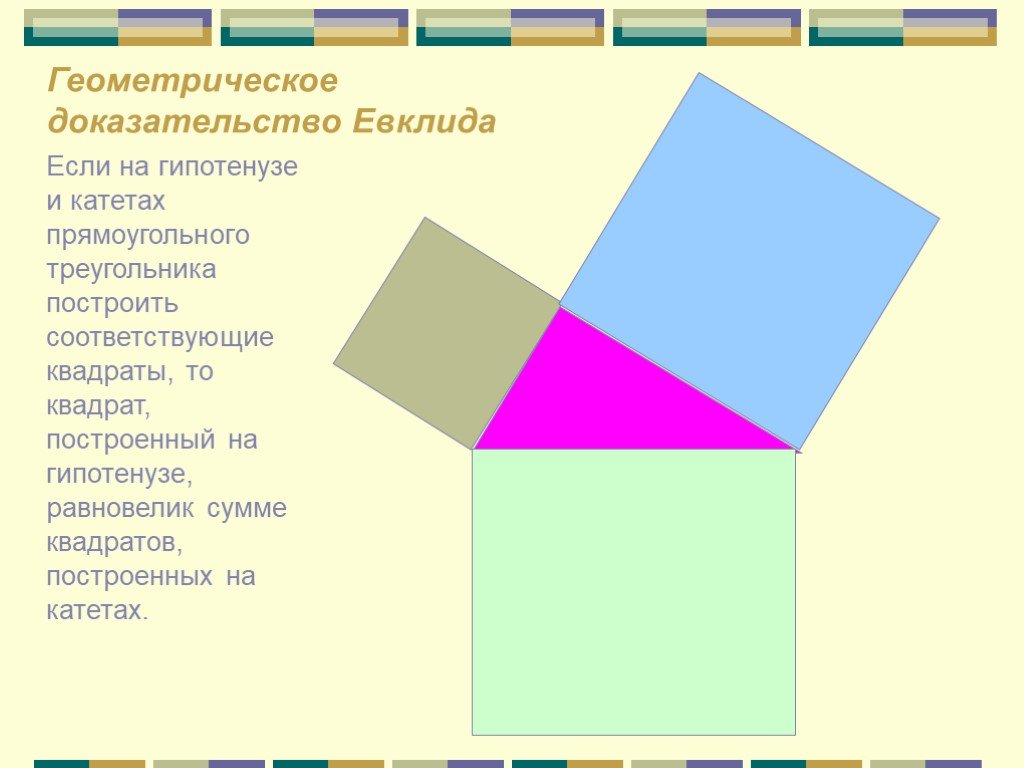
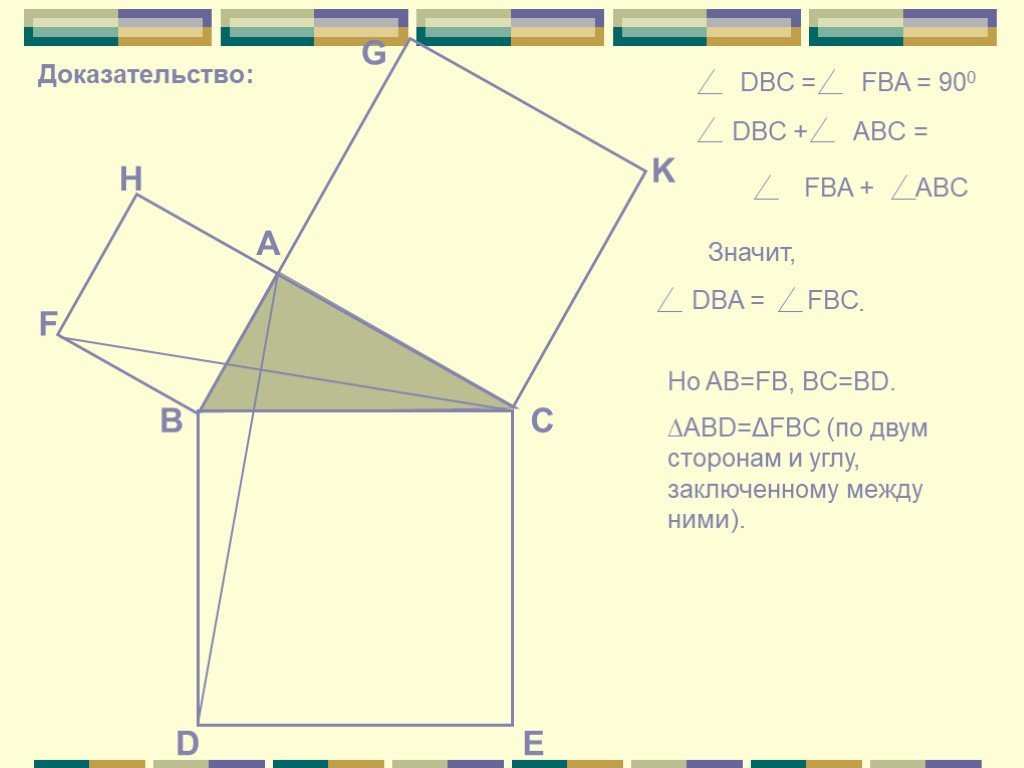
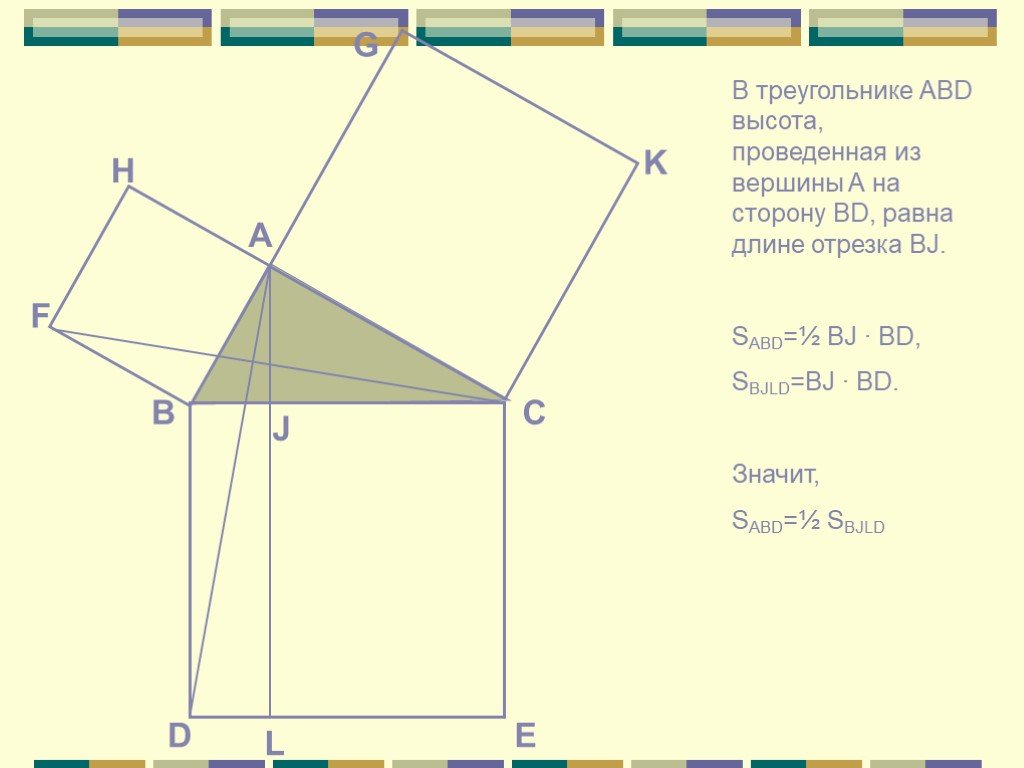
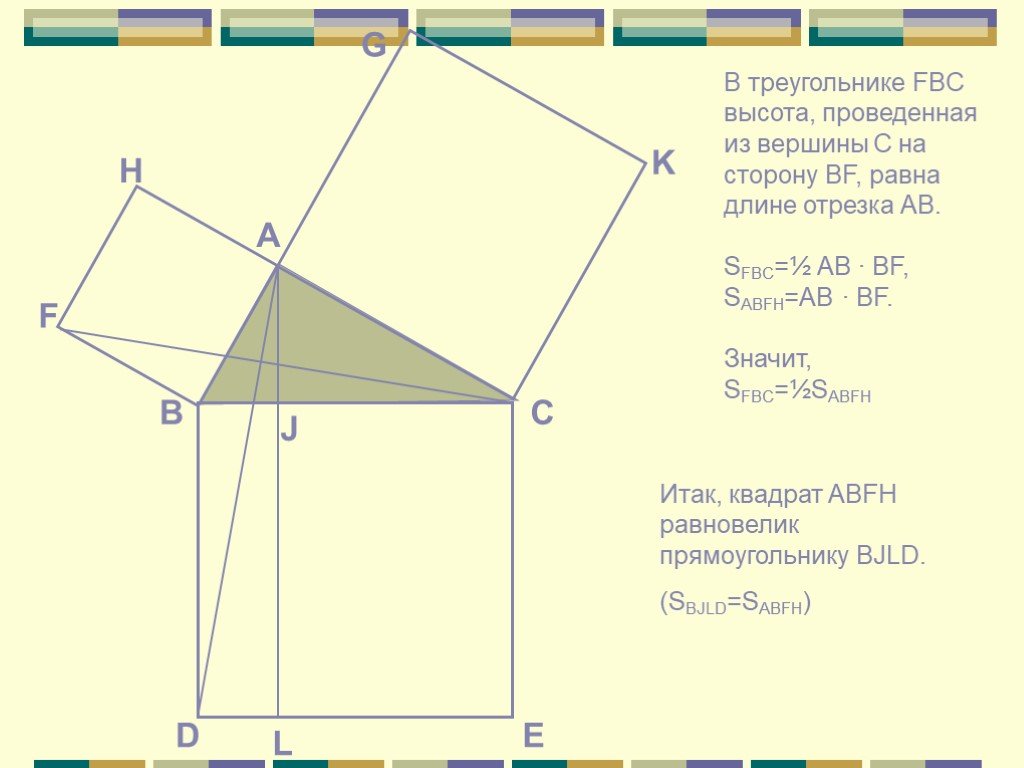
Презентация "Различные подходы к доказательству теоремы Пифагора" по математике – проект, доклад
Презентацию на тему "Различные подходы к доказательству теоремы Пифагора" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
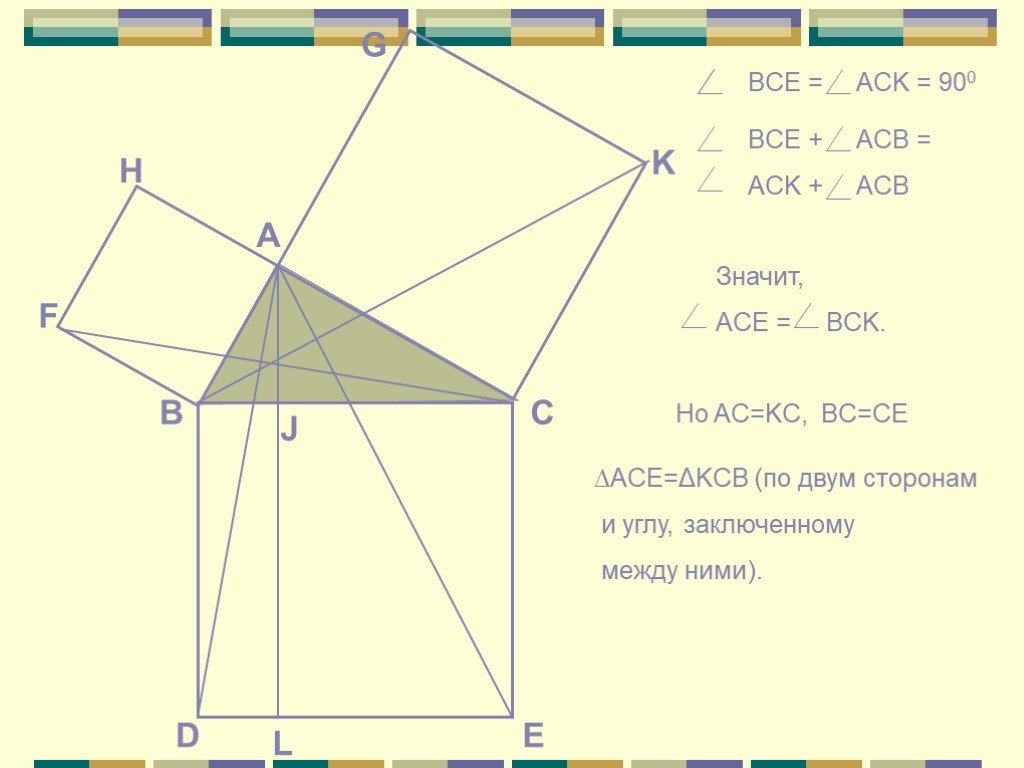
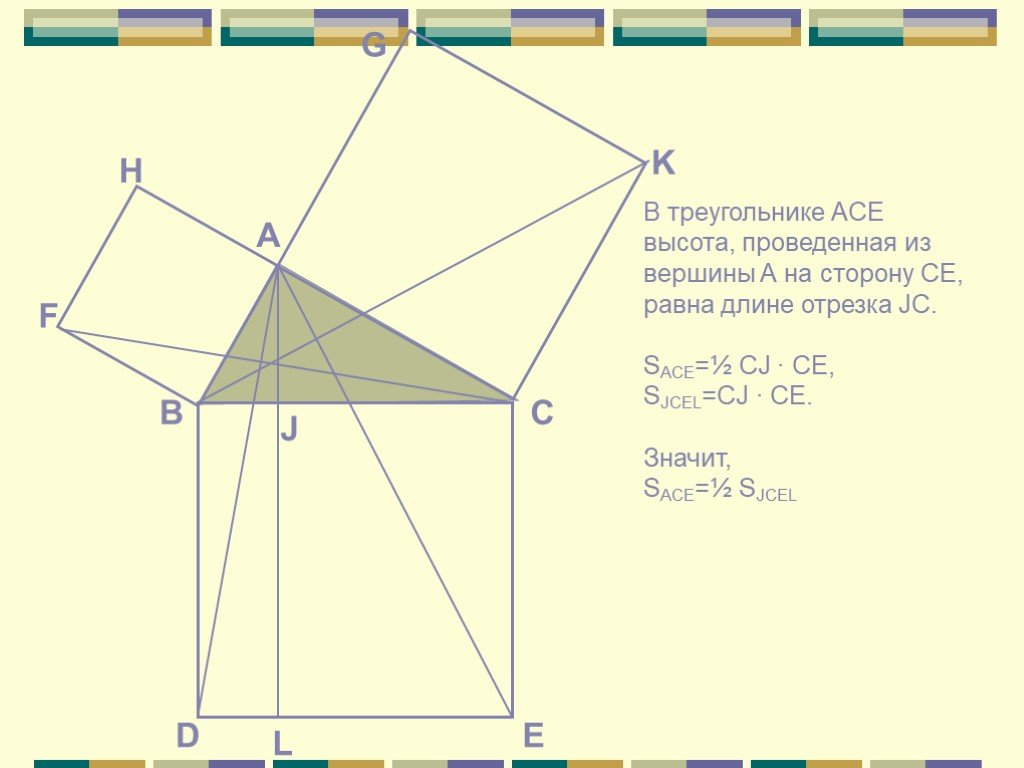
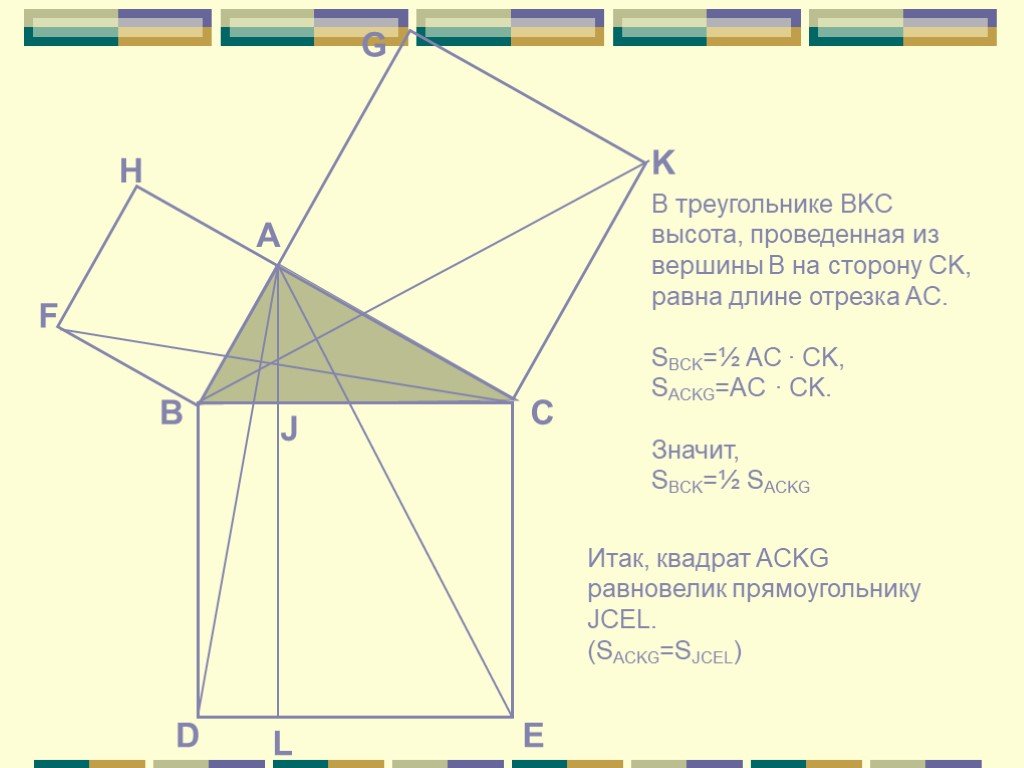
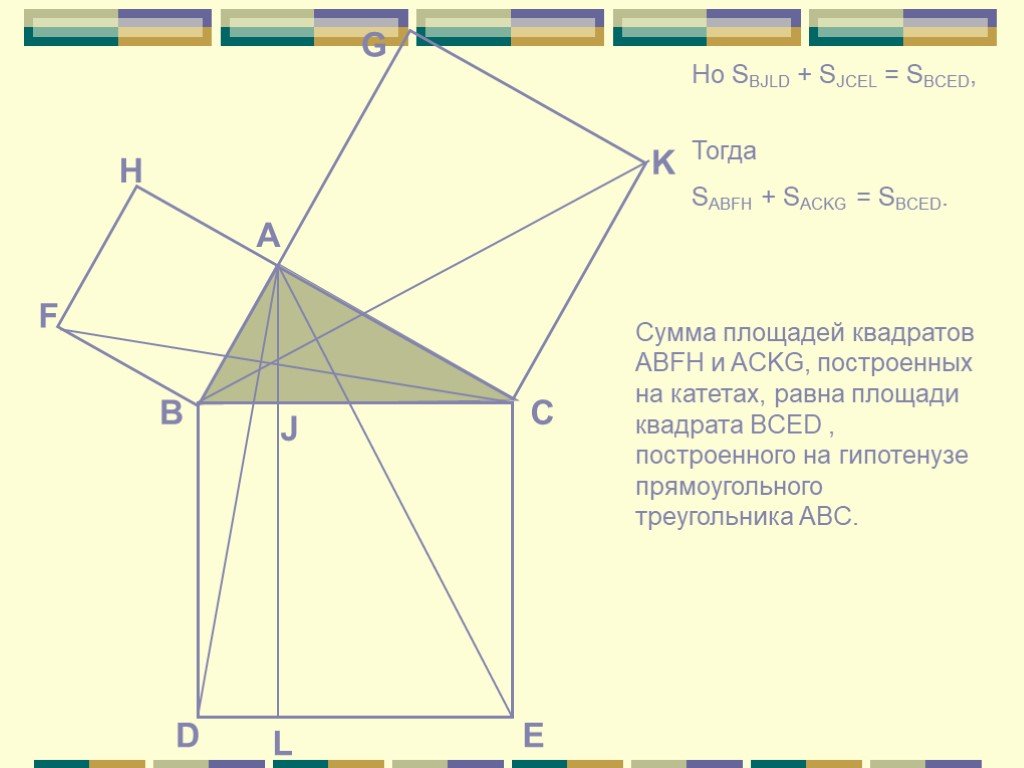
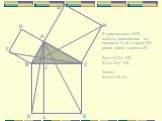
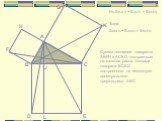
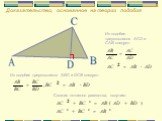
Cпособы доказательства теоремы Пифагора
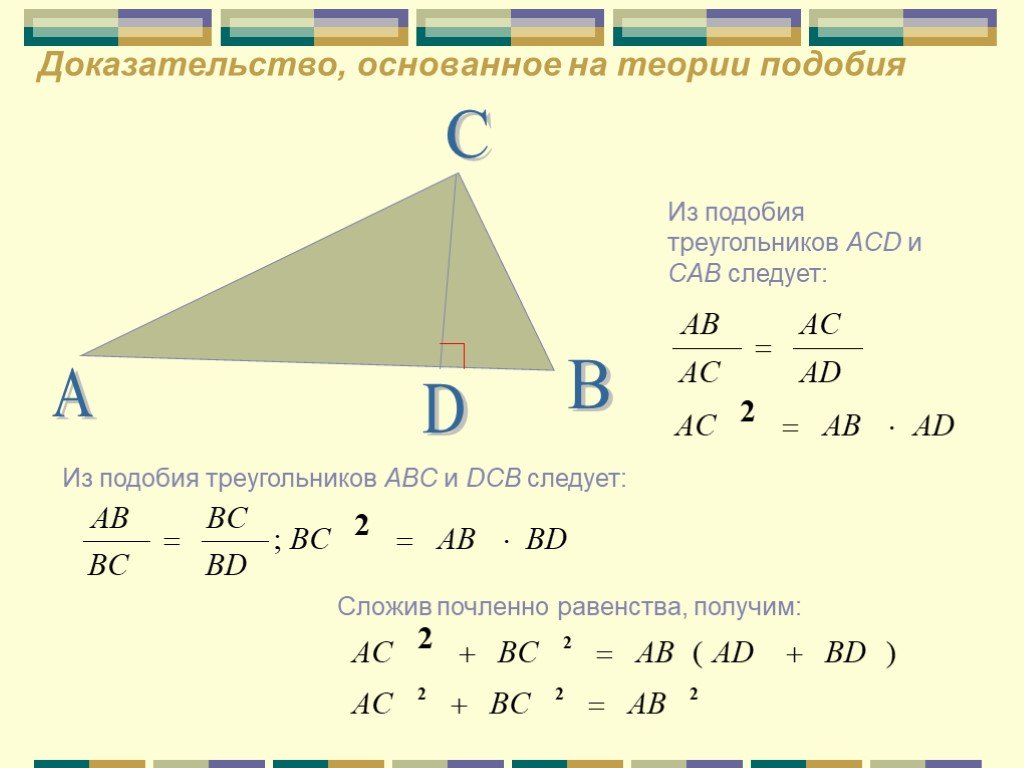
a2+b2=c2 c a b П. Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым ...«Устный счёт» математика
1- 0,4 3 +2,4 3,2 – 2 3,2- 0,2 12,3 + 3,4 2,04 + 3,6 12 – 1,5 6,2- 2,6 ( 12,4 + 3,67)- 2,67 ( 45,06 + 23,5) – 40 ,06. 0,6 5,4 1,2 3 15,7 5,64 10,5 ...«Углы» математика
Цель урока:. познакомить учащихся с геометрической фигурой углом, с видами углов (прямой, тупой, острый), сформировать представления о существенных ...«Своя игра» математика
Математическая игра-викторина «Своя игра». Конец игры Литература. Задачи – шутки 50. Вопрос: Один господин написал о себе: «Пальцев у меня двадцать ...«Своя игра» математика
Условия игры:. Участники сами выбирают темы и вопросы. Вопрос выбирает правильно ответившая команда. 210 – 250 баллов – отметка «5». 110 -200 баллов ...«Координатная плоскость» математика
Цели и задачи урока:. 1. Ввести понятие координатной плоскости, уметь определять координаты точек, строить точки по их координатам. 2. Развивать мышление, ..."Электрики и математика"
Воспитательные Воспитание умения работать в команде, уважения к сопернику, воспитание чувства ответственности; Воспитание чувства ответственности, ...«Математический бой. Через тернии к звездам»
. Разминка. Сколько разных букв в названии нашей страны? 5 букв. ДВЕНАДЦАТЬ. К семи прибавить пять. Как правильно записать: одиннадцать или адиннадцать? ...Конспекты
Алгебраические выражения. Подготовка к экзаменам
Государственное бюджетное специальное (коррекционное) образовательное учреждение для обучающихся, воспитанников с ограниченными возможностями здоровья ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:22 сентября 2019
Категория:Математика
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию