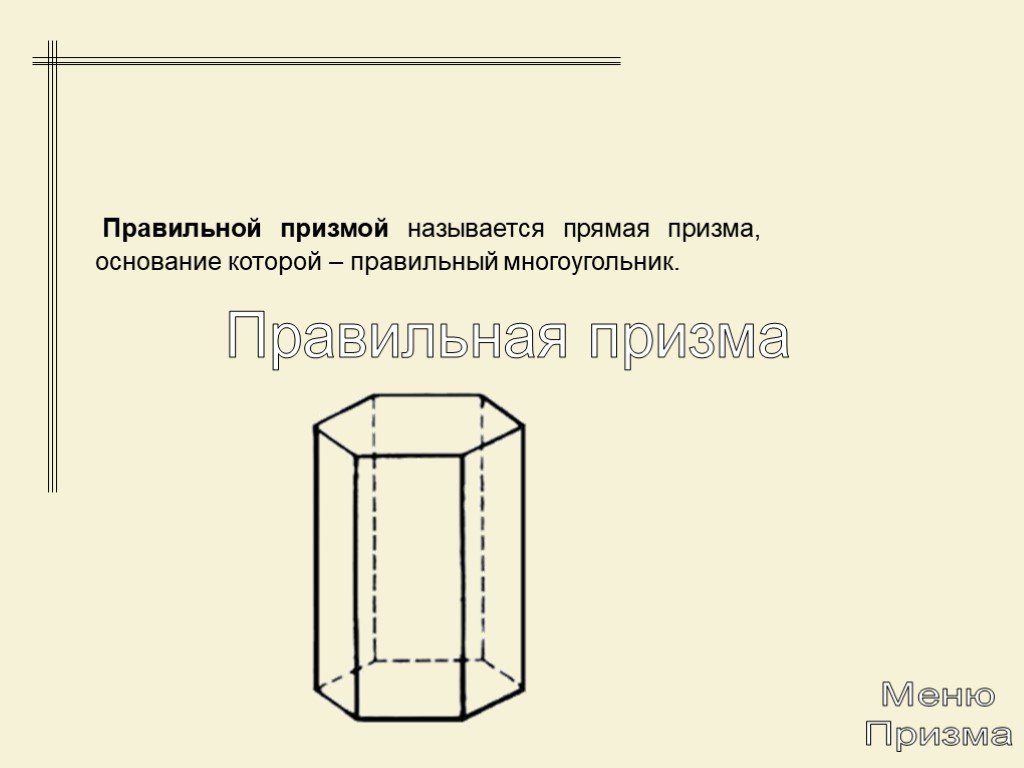
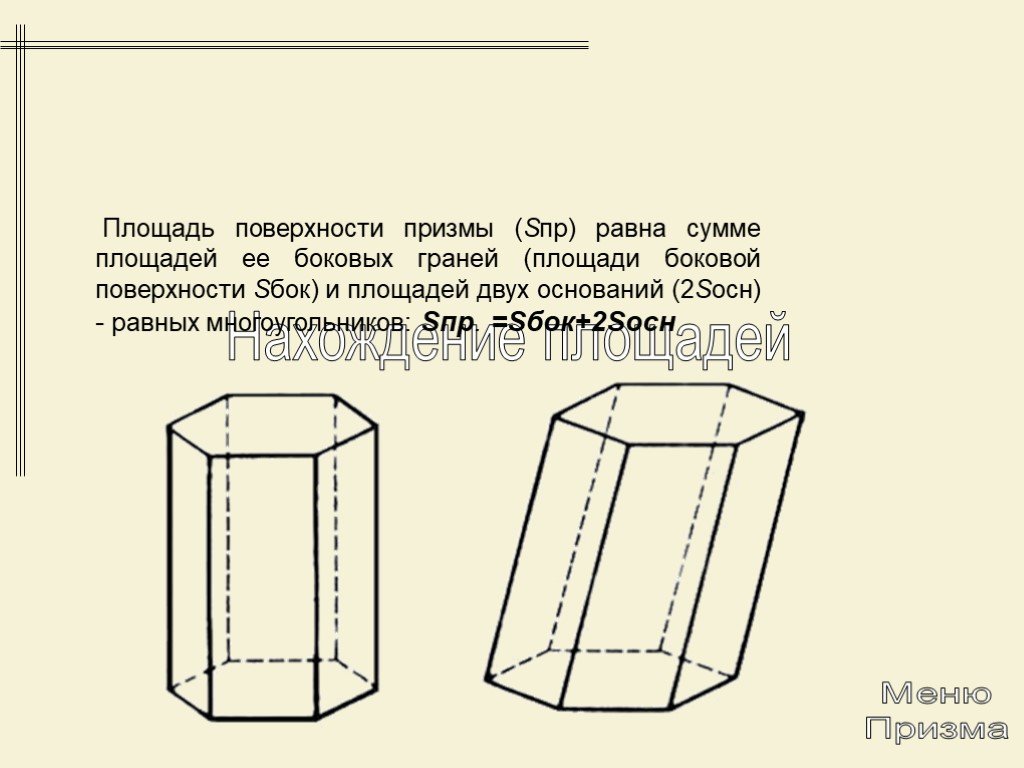
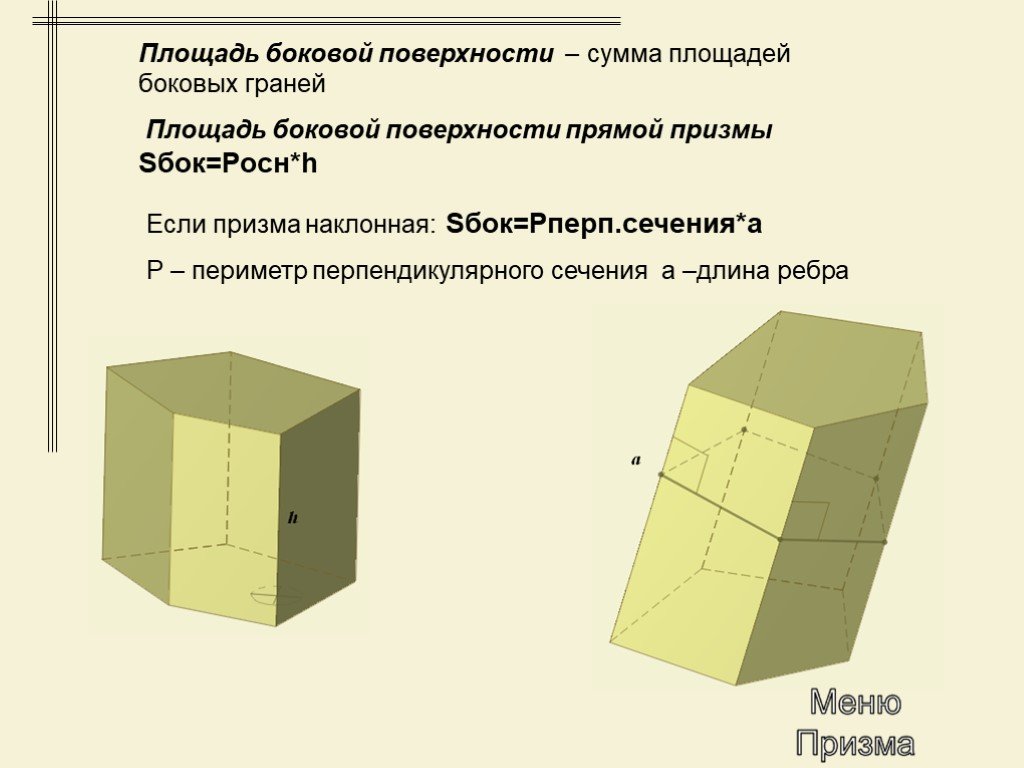
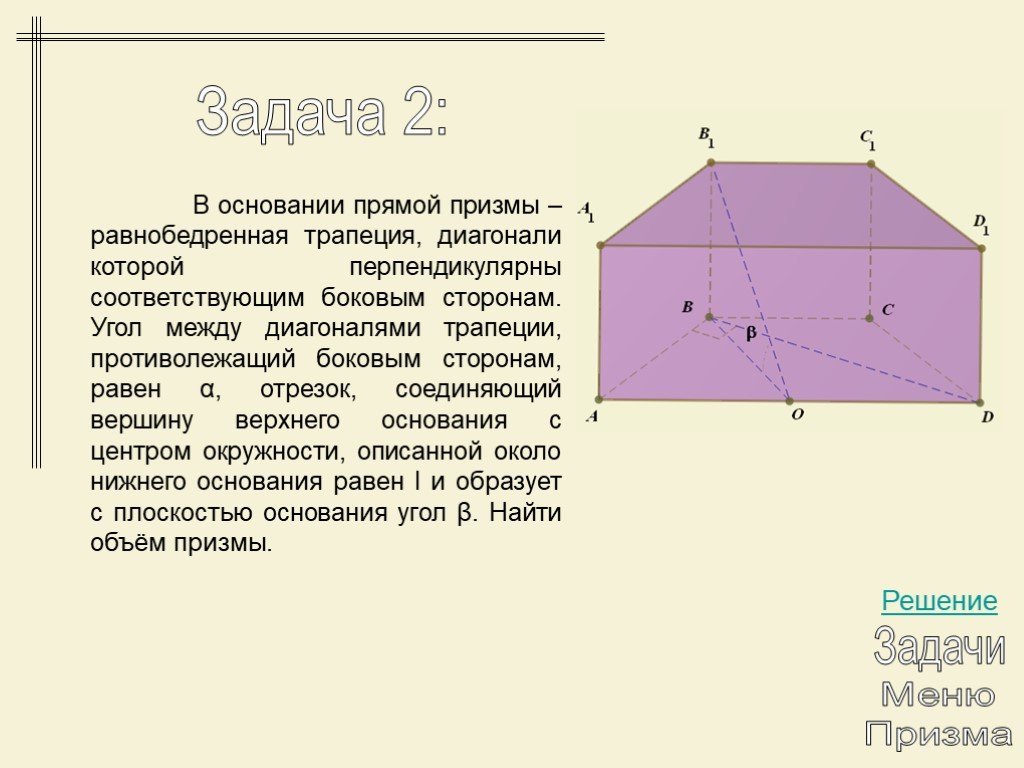
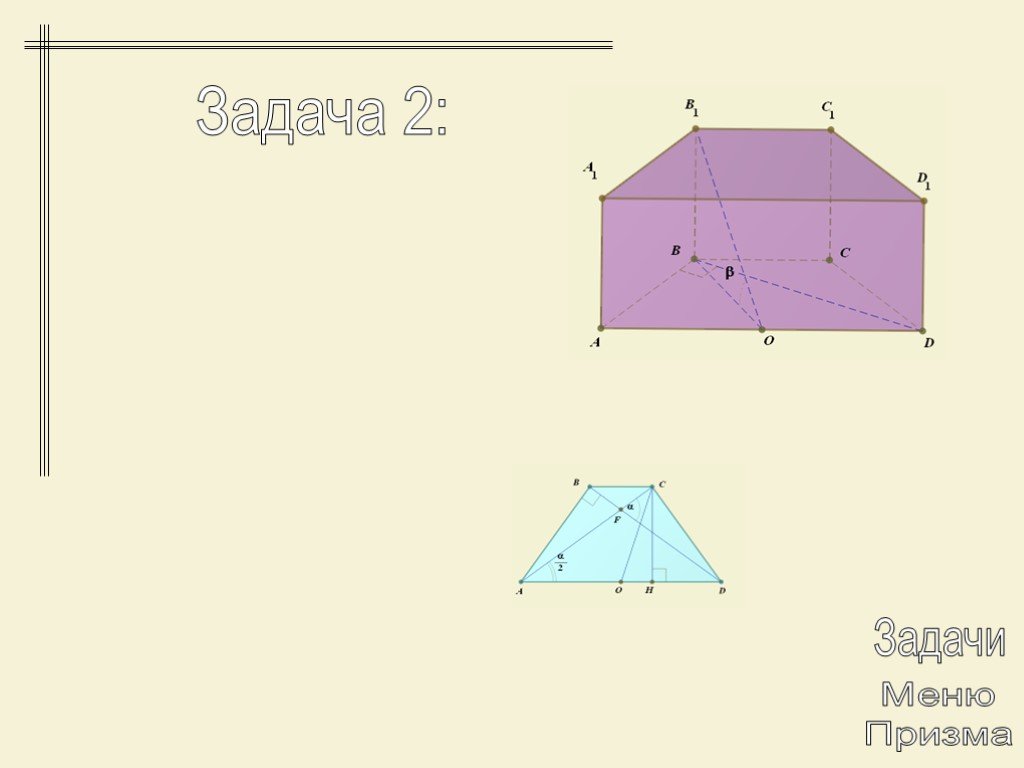
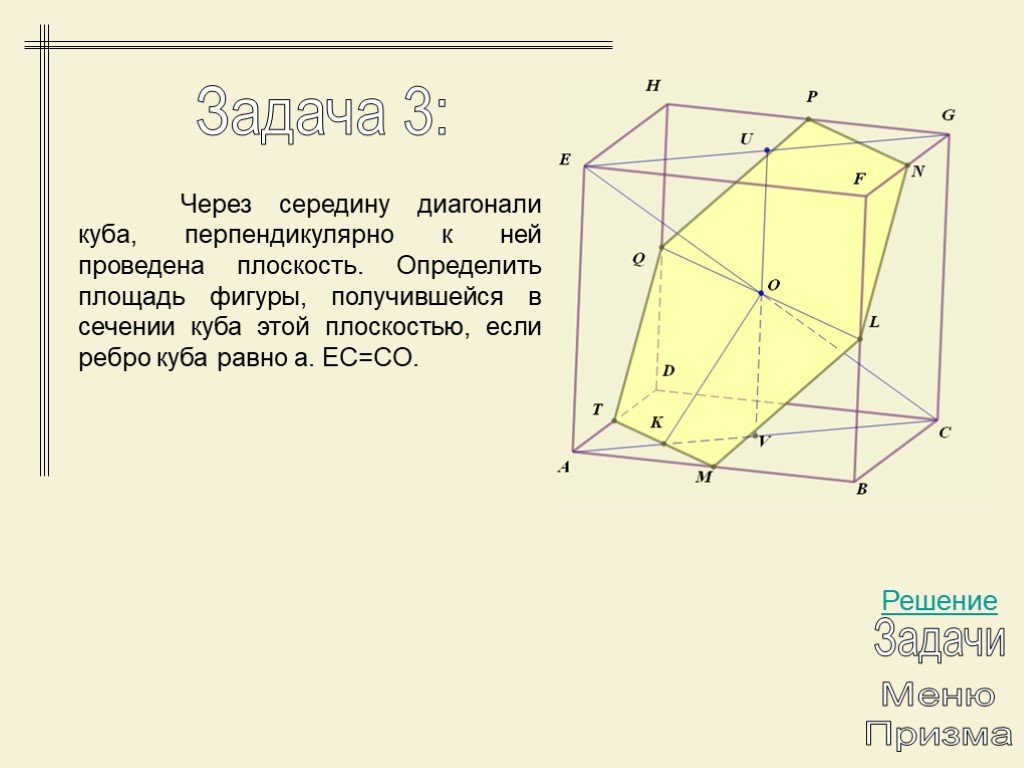
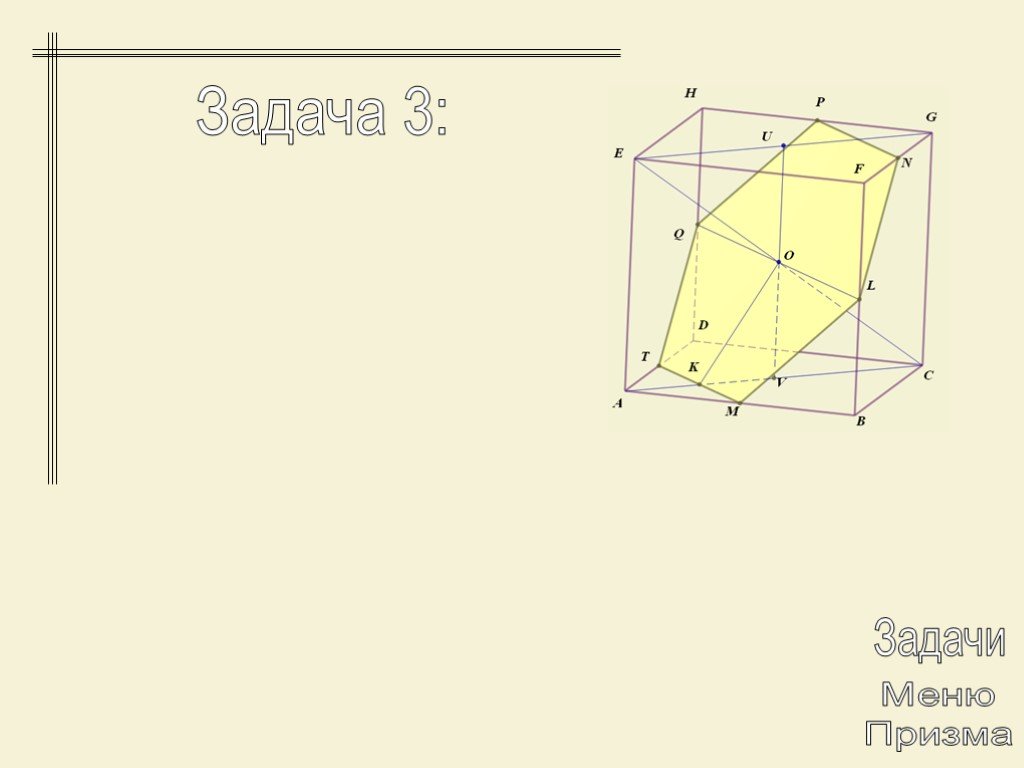
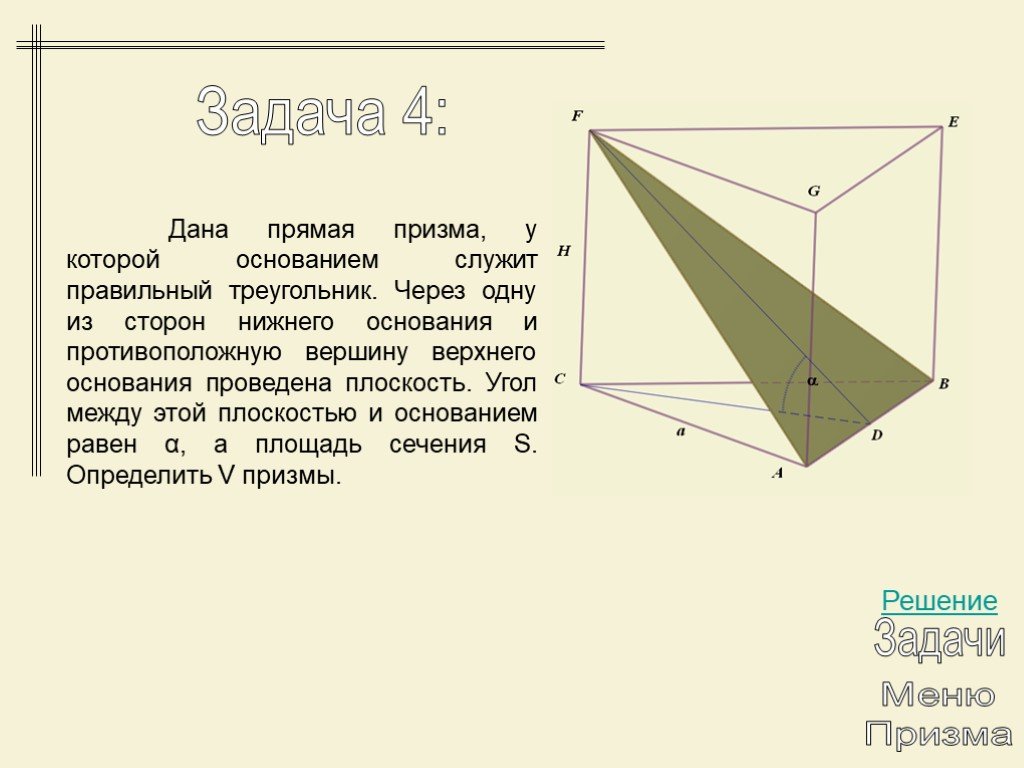
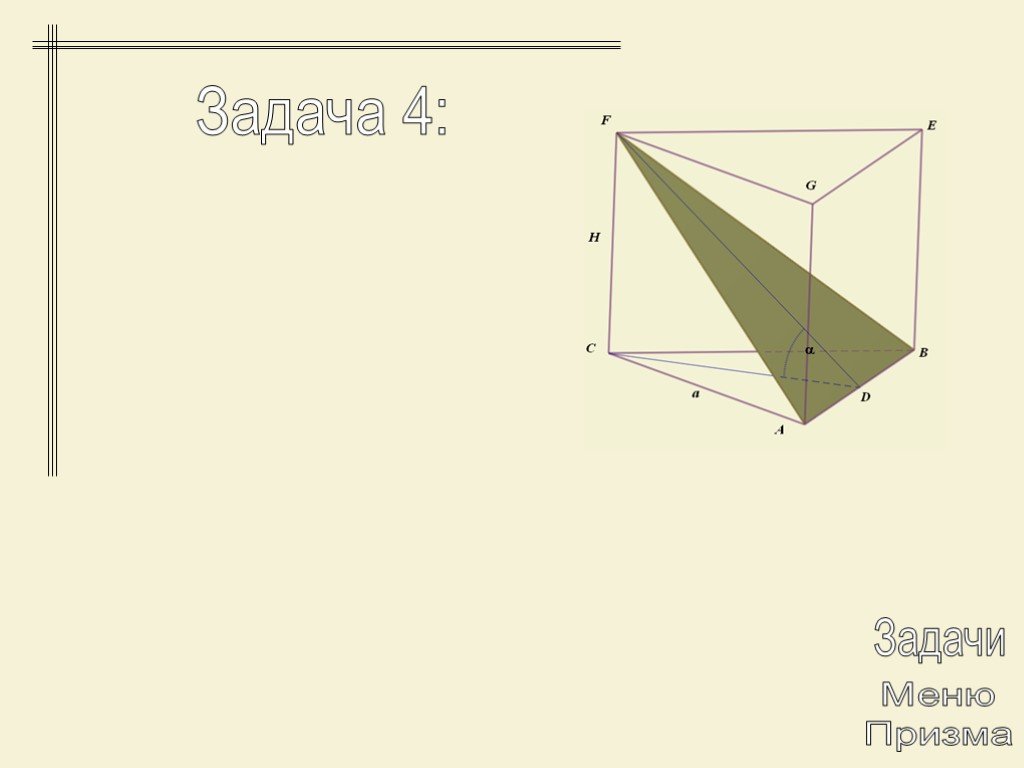
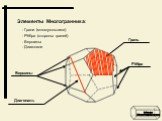
Презентация "Многогранники. Призма" по математике – проект, доклад
Презентацию на тему "Многогранники. Призма" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 28 слайд(ов).
Слайды презентации
Список похожих презентаций
Геометрия в жизни Многогранники
Александрийский маяк. В 285 году до н.э.на острове Фарос архитектор Сострат Книдский приступил к строительству маяка. Маяк строился пять лет и получился ...Призма и ее виды
Решётка железа Решётка магния. Аквариум. Башня Смоленской крепости. Обелиск Беседка. Призма. α β || A B C1 D A1 B1 D1 C ABCDA1B1C1D1 - призма. Верхнее ...Призма и ее свойства
Содержание. Историческая справка Призма и ее свойства Решение задач Задачи для самостоятельной работы Литература. Историческая справка. Еще в древности ...Призма
АВТОРЫ: Дёмина Ирина - 10 Б класс , Дёмина Юлия - 10 Б класс , Нагачеева Екатерина - 10 Б класс. Научный консультант - учитель математики Петелина ...Призма
Определение призмы:. А1А2…АnВ1В2Вn– призма Многоугольники А1А2…Аn и В1В2…Вn – основания призмы Параллелограммы А1А2В2В1, А1А2В2В1,… АnА1В1Вn – боковые ...Многогранники вокруг нас
«Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, ...Многогранники
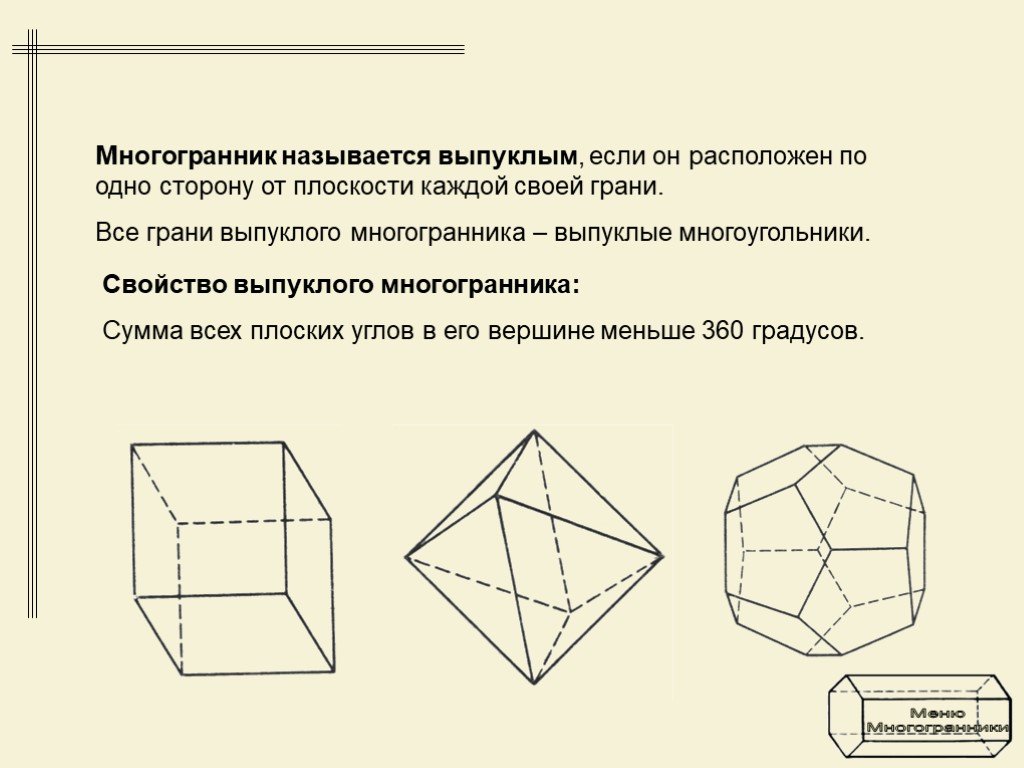
Выпуклые многогранники. Многогранник называется выпуклым, если он является выпуклой фигурой, т.е. вместе с любыми двумя своими точками целиком содержит ...Многогранники
Тетраэдр. Тетраэдр, или треугольная пирамида, - простейший из многогранников, подобно тому как треугольник - простейший из многоугольников на плоскости. ...Многогранники
Здравствуйте! Начинаем урок! Разминка: запиши одним словом! Геометрическая фигура, у которой три стороны, три угла и три вершины. Четырёхугольник, ...Многогранники
Дома:. стр. 80 – 81, п. 51 Приготовить презентацию. Математический диктант. Оцените себя. 4-5 заданий – «3» 6-7 заданий – «4» 8 заданий – «5». 1. ...Многогранники
ВСПОМНИМ. Какую фигуру в планиметрии мы называли многоугольником? Тетраэдр. Тетра (греч.) - четыре. Цели. Ввести понятие тетраэдра Рассмотреть его ...Многогранник Призма
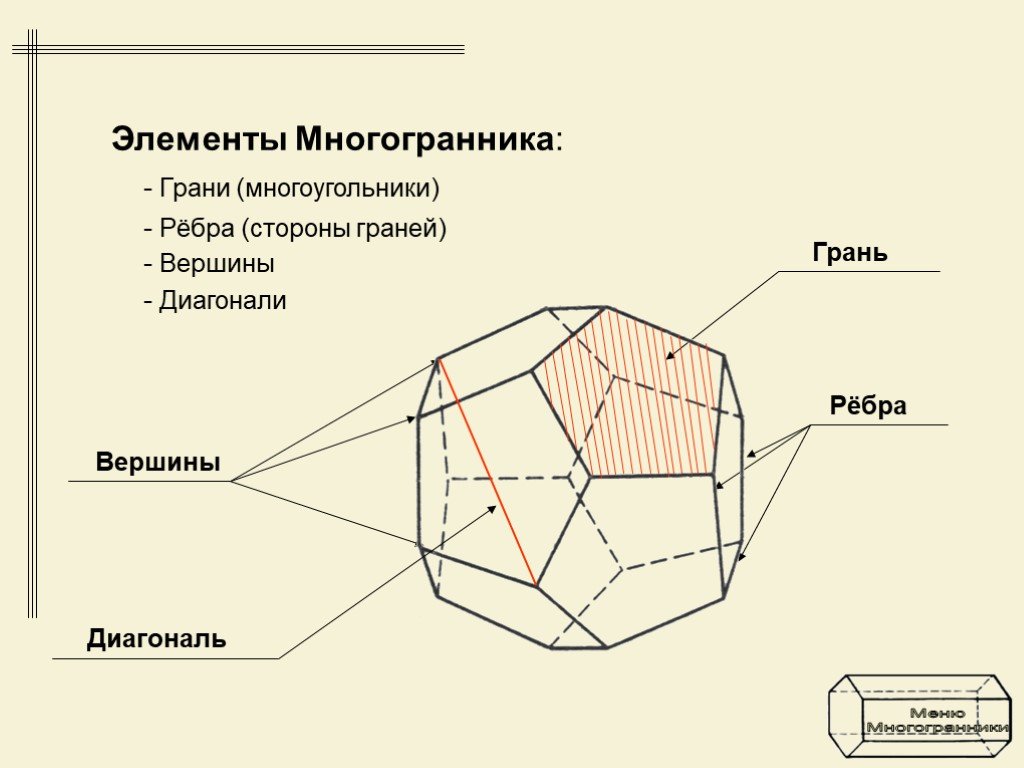
ПРОСТРАНСТВО многогранники выпуклые невыпуклые. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют ...Задача В-9 ЕГЭ. Многогранники
Условие. Найдите угол ЕАД2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Построим треугольник ...Многогранники вокруг нас
Общий исторический обзор Первые геометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: ...Многогранники
Содержание презентации. Изображение многогранников. Многогранные формы с древнейших времен преобладают в архитектуре и строительстве. В русском зодчестве ...Многогранники вокруг нас
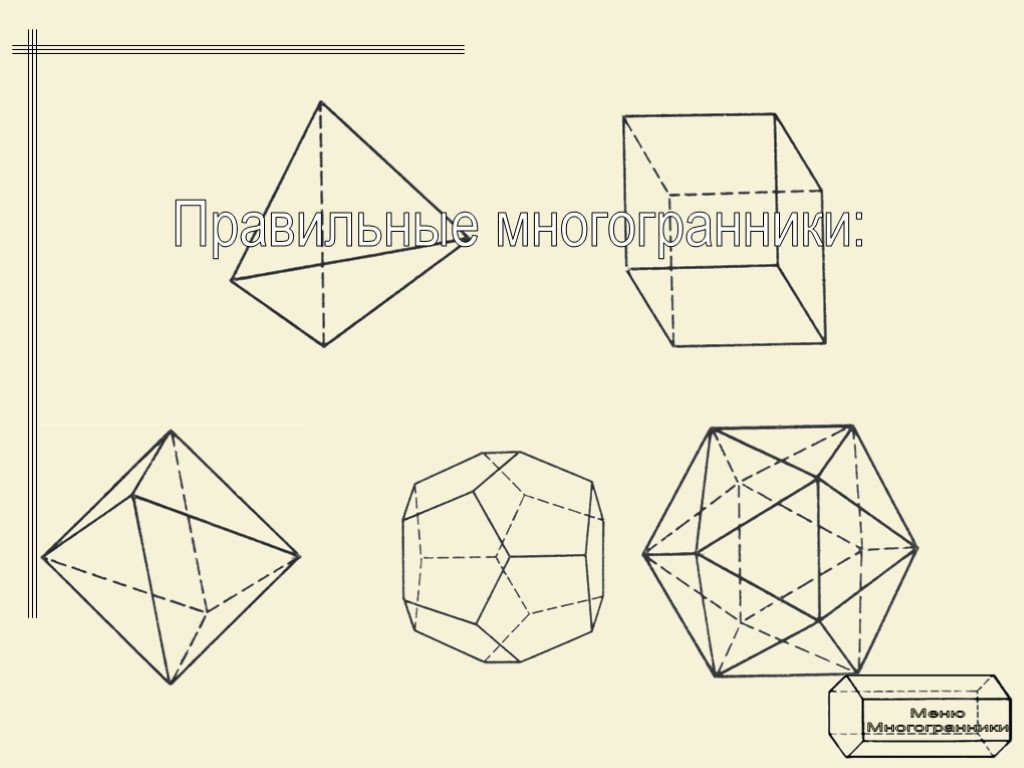
Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. "Правильных многогранников вызывающе мало, - ...Многогранники
Многогранник - часть пространства, ограниченная совокупностью конечного числа плоских многоугольников соединенных таким образом, что каждая сторона ...Многогранники и кристаллы
Содержание. Многогранный угол Кристаллы Кристаллы различных веществ Драгоценные камни Рубин Сахарная свекла От создателя. Актуальность. Молекулы кристаллов ...Многогранники
Параллелепипед ||. АВСD и A1B1C1D1 – равные параллелограммы – основания АА1|| ВВ1|| СС1|| DD1 – боковые ребра Все грани параллелограммы. AA1B1B; BB1C1C; ...Конспекты
Многогранники
. Министерство образования Нижегородской области. Государственное бюджетное образовательное учреждение среднего профессионального образования. ...Многогранники и тела вращения. Их площади и объемы
Урок геометрии 11 класс «Многогранники и тела вращения. Их площади и объемы» на основе метода проектов. График работы над проектом:. Подготовительный ...Многогранники
Чалая Елена Александровна,. учитель математики. МБОУ СОШ № 30. г. Краснодар. . Тема урока: «Многогранники». Учебно-методическое обеспечение:. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 мая 2019
Категория:Математика
Содержит:28 слайд(ов)
Поделись с друзьями:
Скачать презентацию