Презентация "Многогранники" по математике – проект, доклад
Презентацию на тему "Многогранники" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
Многогранники вокруг нас
Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, ...Многогранники вокруг нас
Общий исторический обзор Первые геометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: ...Многогранники в архитектуре
Доисторическая архитектура. Менгиры Дольмены Кромлех. Три великих государства древности оказали наибольшее влияние на развитие европейской культуры ...Многогранники в Природе
Кристалл поваренной соли. Кристаллическая решетка поваренной соли имеет кубическую структуру. Кристаллы в форме призм. Рубин Горный хрусталь. Простейшее. ...Геометрия в жизни Многогранники
Александрийский маяк. В 285 году до н.э.на острове Фарос архитектор Сострат Книдский приступил к строительству маяка. Маяк строился пять лет и получился ...Многогранники в архитектуре
При Франциске I было развернуто масштабное строительство, в котором принимали участие как французские, так и приглашенные из Италии архитекторы. В ...Многогранники
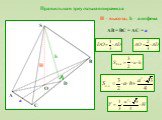
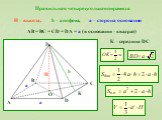
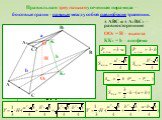
Тетраэдр. Тетраэдр, или треугольная пирамида, - простейший из многогранников, подобно тому как треугольник - простейший из многоугольников на плоскости. ...Многогранники и кристаллы
Содержание. Многогранный угол Кристаллы Кристаллы различных веществ Драгоценные камни Рубин Сахарная свекла От создателя. Актуальность. Молекулы кристаллов ...Многогранники
Дома:. стр. 80 – 81, п. 51 Приготовить презентацию. Математический диктант. Оцените себя. 4-5 заданий – «3» 6-7 заданий – «4» 8 заданий – «5». 1. ...Многогранники
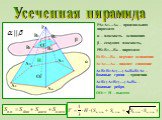
Выпуклые многогранники. Многогранник называется выпуклым, если он является выпуклой фигурой, т.е. вместе с любыми двумя своими точками целиком содержит ...Многогранники
Здравствуйте! Начинаем урок! Разминка: запиши одним словом! Геометрическая фигура, у которой три стороны, три угла и три вершины. Четырёхугольник, ...Многогранники
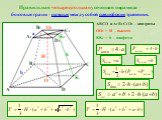
ВСПОМНИМ. Какую фигуру в планиметрии мы называли многоугольником? Тетраэдр. Тетра (греч.) - четыре. Цели. Ввести понятие тетраэдра Рассмотреть его ...Задача В-9 ЕГЭ. Многогранники
Условие. Найдите угол ЕАД2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Построим треугольник ...Многогранники вокруг нас
Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. "Правильных многогранников вызывающе мало, - ...Многогранники
Содержание презентации. Изображение многогранников. Многогранные формы с древнейших времен преобладают в архитектуре и строительстве. В русском зодчестве ...Многогранники вокруг нас
«Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, ...Многогранники
Многогранник - часть пространства, ограниченная совокупностью конечного числа плоских многоугольников соединенных таким образом, что каждая сторона ...Геометрические тела. Многогранники
Многообразие геометрических форм вокруг нас на примере зданий. Геометрические тела. 7. Куб (гр. kymbos) Чаша, горшок 4. Цилиндр (гр. cylindrus) Валик ...Конспекты
Многогранники
. Министерство образования Нижегородской области. Государственное бюджетное образовательное учреждение среднего профессионального образования. ...Многогранники и тела вращения. Их площади и объемы
Урок геометрии 11 класс «Многогранники и тела вращения. Их площади и объемы» на основе метода проектов. График работы над проектом:. Подготовительный ...Многогранники
Чалая Елена Александровна,. учитель математики. МБОУ СОШ № 30. г. Краснодар. . Тема урока: «Многогранники». Учебно-методическое обеспечение:. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию