Презентация "Двугранный угол" по математике – проект, доклад
Презентацию на тему "Двугранный угол" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 21 слайд(ов).
Слайды презентации
Список похожих презентаций
Двугранный угол. Угол между плоскостями2
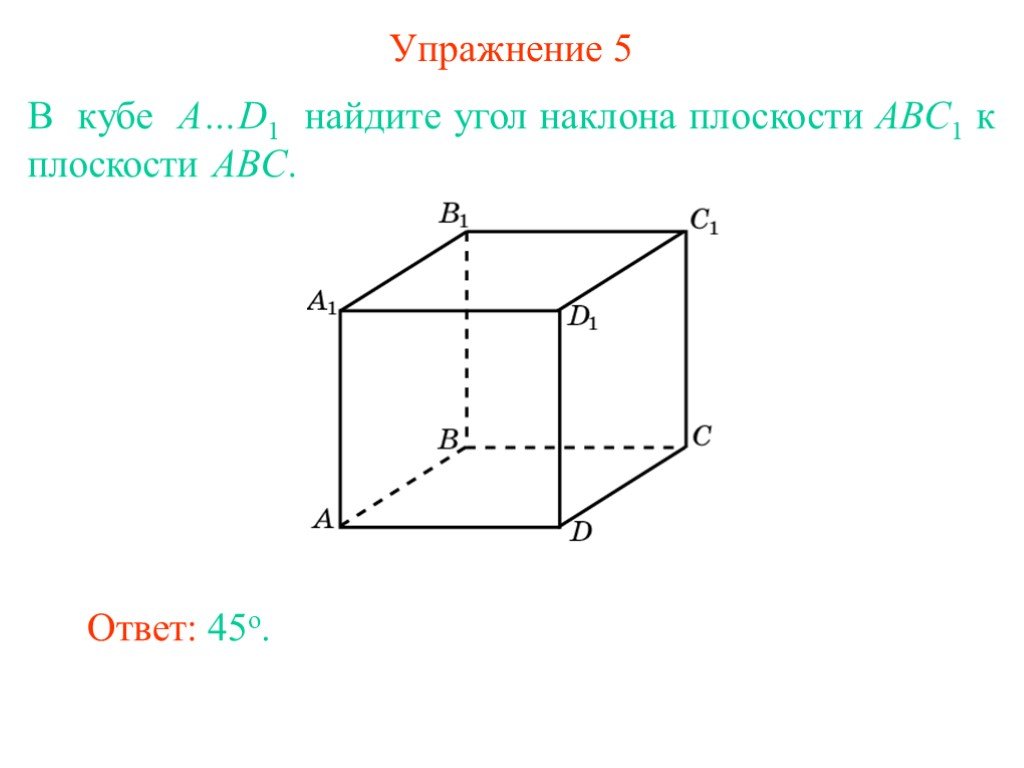
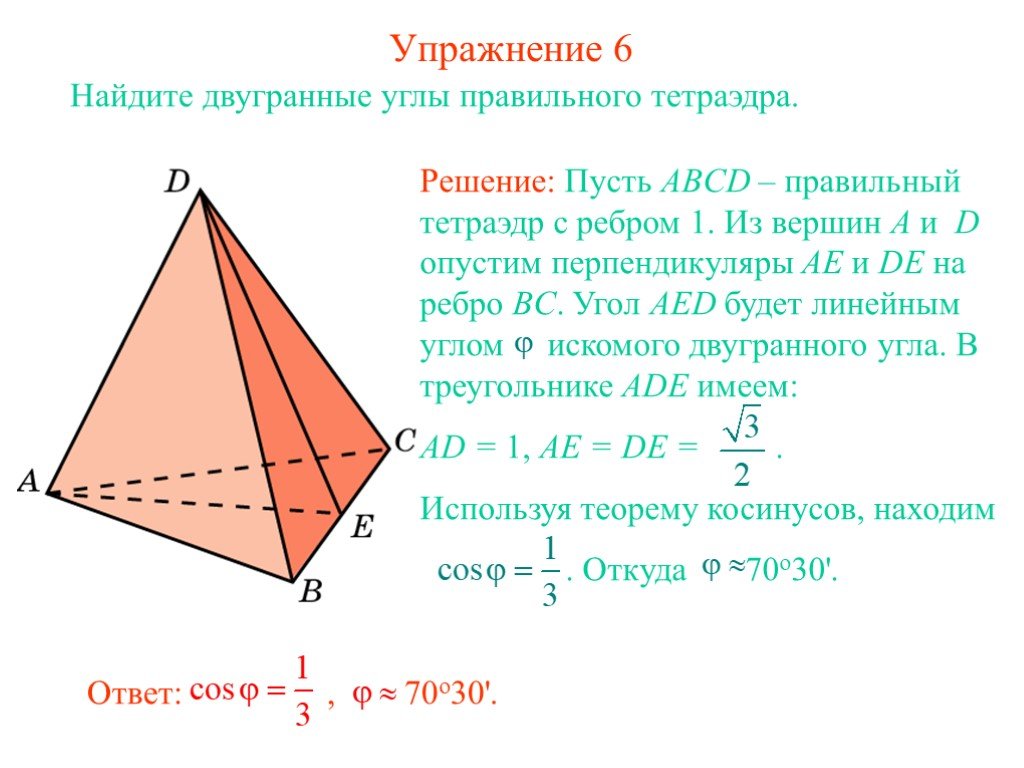
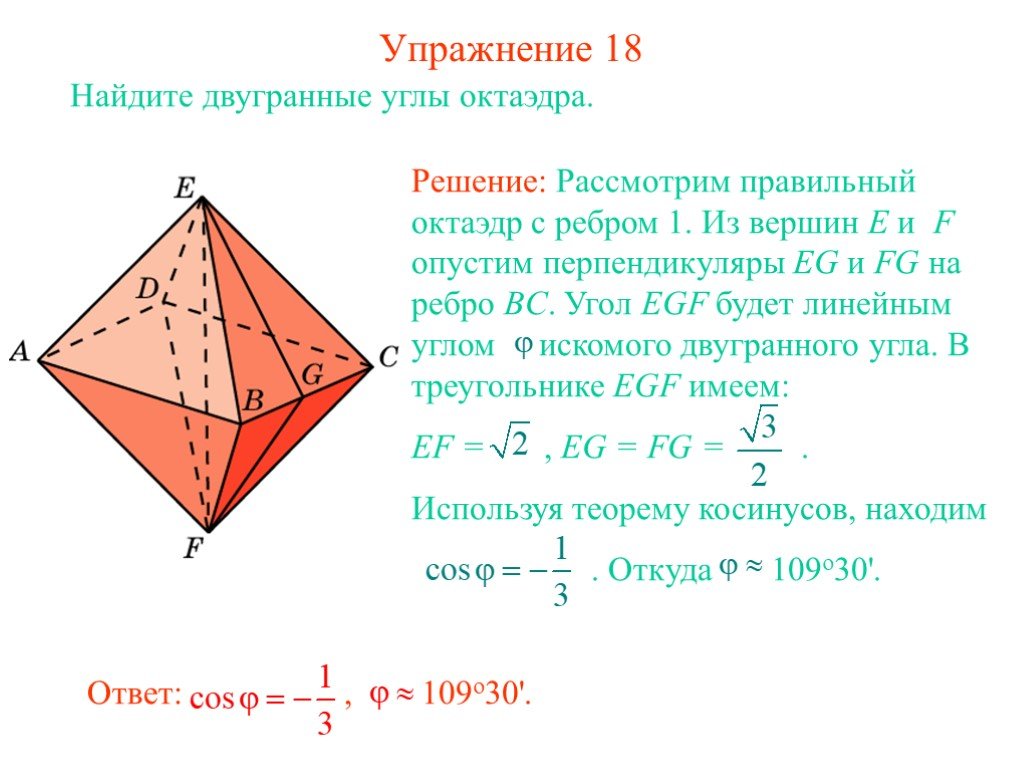
В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD. В правильной пирамиде SABCD, все ребра которой равны 1, найдите ...Двугранный угол
Вдохновение есть расположение души к живейшему принятию впечатлений и соображению понятий, следственно, и объяснению оных. Вдохновение нужно в геометрии, ...Двугранный угол. Угол между плоскостями
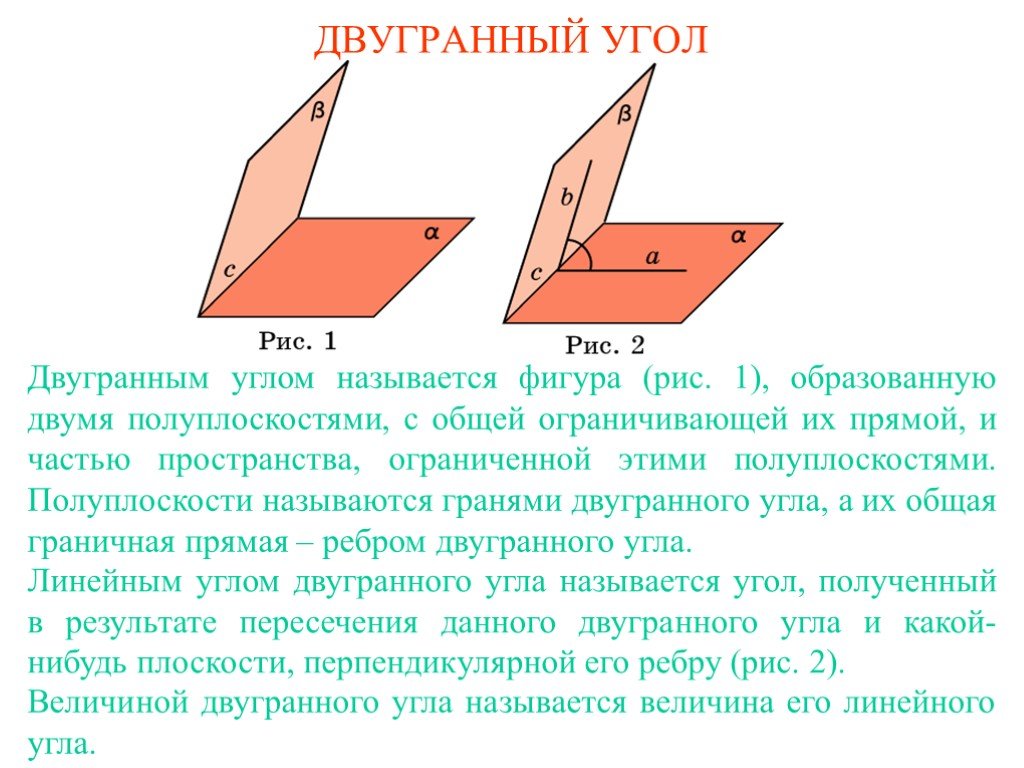
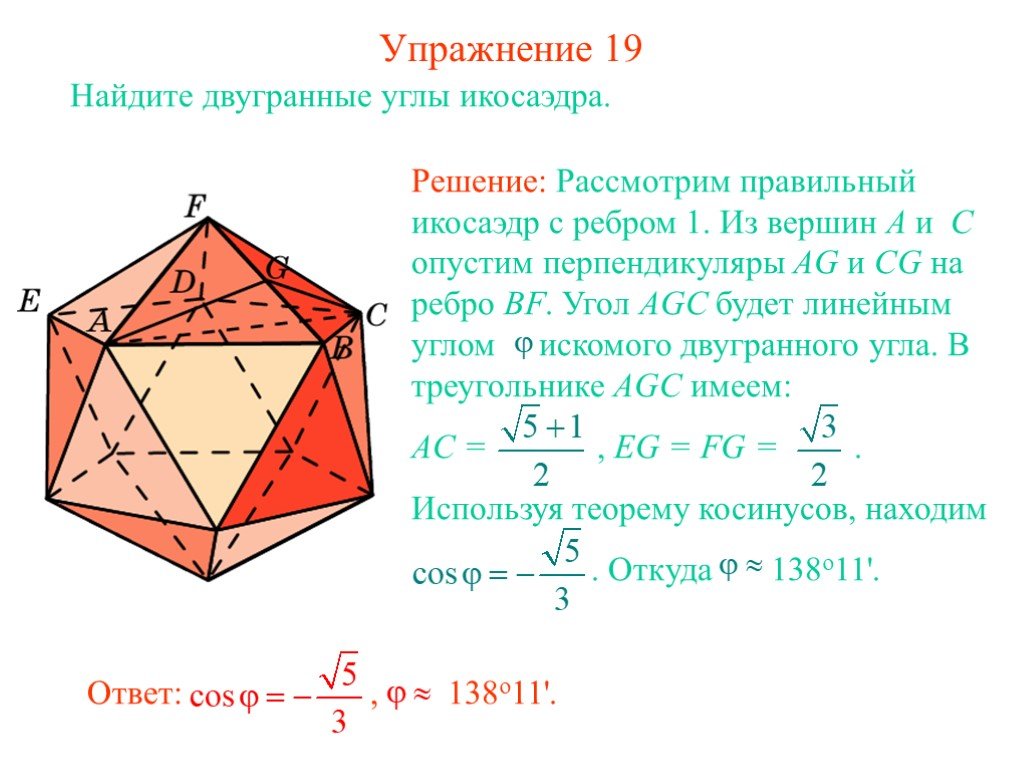
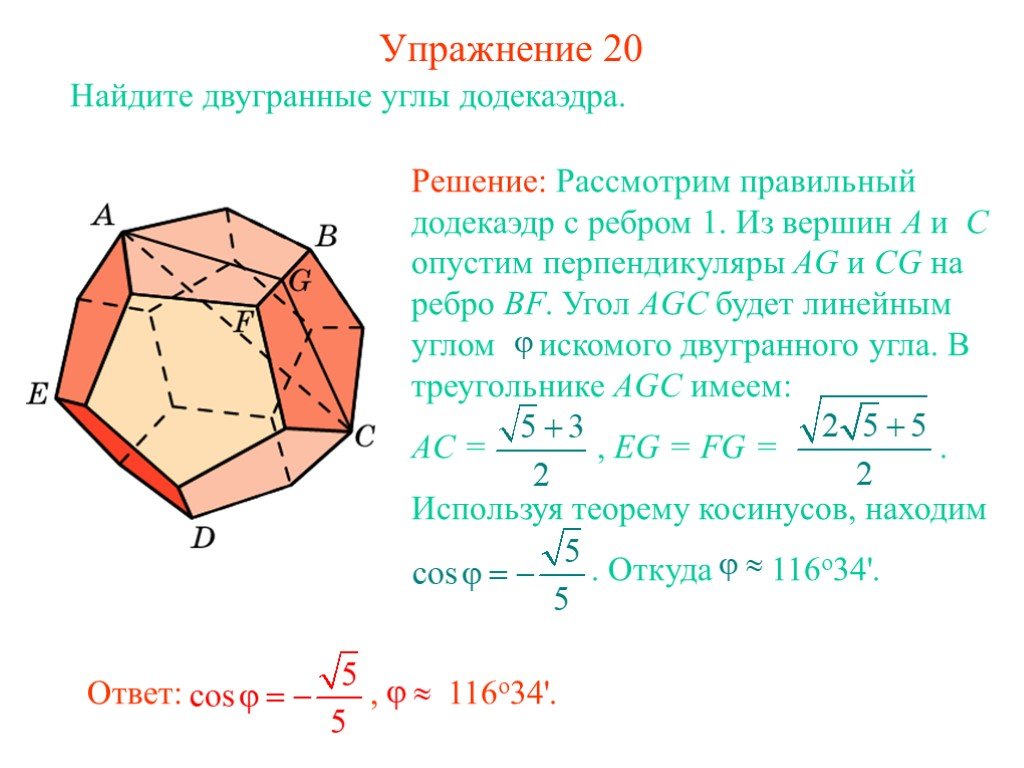
Основные понятия. Прямая а разделяет плоскость на две полуплоскости. Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями ...Двугранный угол
Основные задачи урока:. Ввести понятие двугранного угла и его линейного угла Рассмотреть задачи на применение этих понятий. Определение:. Двугранным ...Внешний угол треугольника. Теорема о внешнем угле треугольника
I. Cумма углов треугольника. 1. На доске доказать теорему о сумме углов треугольника: Сумма углов треугольника равна 1800 2. Решить задачу № 749 (чёт ...Внешний угол треугольника
Общий вид внешнего угла. Понятие. Свойство внешнего угла. Внешний угол. Внешний угол треугольника. Угол, смежный с каким–нибудь углом треугольника, ...Луч и угол
Часть1. РЕШЕНИЕ ЗАДАЧ НА ПОВТОРЕНИЕ:. Дайте определение отрезка Какие понятия в геометрии считаются неопределимыми? Чем отличается теорема от аксиомы? ...Начальные понятия планиметрии. Прямая и отрезок. Луч и угол
Вводная беседа.Геометрия в переводе с греческого «землемерие» («гео»- по-гречески земля, а «метрео» - мерить).
Первым, кто начал получать геометрические ...
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Теорема 2. В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны ...Внешний угол треугольника
Треугольник (музыкальный инструмент). Жесткость треугольников. Бермудский треугольник. ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА. У треугольника может быть два тупых ...Математика геометрия
ГЛАВА 1. История математики. ГЛАВА 2. Математика. ГЛАВА 3. Геометрия И последнее…. Что такое математика. Она изучает числа и величины, отношения и ...Лобачевский и его геометрия
Гипотеза:. Любая теория современной науки считается единственно верной, пока не создана следующая. Невозможность доказать некоторое геометрическое ...Зачем нужна наука геометрия?
Что означает термин геометрия??? Из истории возникновения геометрии. Где изучают геометрию? Виды углов. Виды треугольников. Зачем нужна геометрия??? ...Занимательная геометрия
КРОССВОРД Т О Ч К А. П Р Я М О Й. О Т Р Е З О К. О К Р У Ж Н О С Т Ь. К В А Д Р А Т. Л У Ч. На каком из рисунков клеточки А2, В1, С3 закрашены? На ...Живая геометрия
Цель проекта :. - создание художественно-оформительной студии Пютагорас; Коллекция открыток и коллекция ювелирных изделий. Задачи проекта :. Образовательные: ...геометрия решение задачи
Дано: а-прямая, A B а Построить: BC=2AB Решение:. A,B-точки на прямой,. (на луче BA). Измерим циркулем расстояние между A и B,. отложим отрезок AC ...Все вокруг - геометрия
Откуда есть, пошла «Геометрия»? Слово «геометрия» - греческое, в переводе на русский означает «землемерие». около 4000 лет тому назад жители Древнего ...Наглядная геометрия
геометрия Урок 1. Сегодня мы отправляемся в путешествие в удивительную страну, которая называется ГЕОМЕТРИЯ. Что такое геометрия? Какими инструментами ...Наглядная геометрия для начальной школы
Содержание. Урок 1 Урок 2 Урок 3 Урок 4. Урок 1 Путешествие в страну Геометрия. Знакомство с веселой Точкой. Начнем урок. Наша школьная страна. Не ...«Конус» геометрия
История изучения геометрического тела конус. С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки. ...Конспекты
Двугранный угол
Тема урока: «Двугранный угол». Ф.И.О. учителя:. Банникова Дарья Дмитриевна. Дата проведения:. 26.02.13. Класс:. 10 «Б». . Цели урока:. Ввести ...Прямой и непрямой угол
Тема: Прямой и непрямой угол. . Цели урока:. *познакомить с прямым и непрямым углом;. . *закреплять вычислительные навыки;. . *развивать ...Виды углов. Прямой угол
Автор: Малахова Галина Григорьевна, учитель начальных классов МКОУ СОШ № 17 села Сухая Буйвола, Петровского района, Ставропольского края. . Виды ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:10 августа 2019
Категория:Математика
Содержит:21 слайд(ов)
Поделись с друзьями:
Скачать презентацию