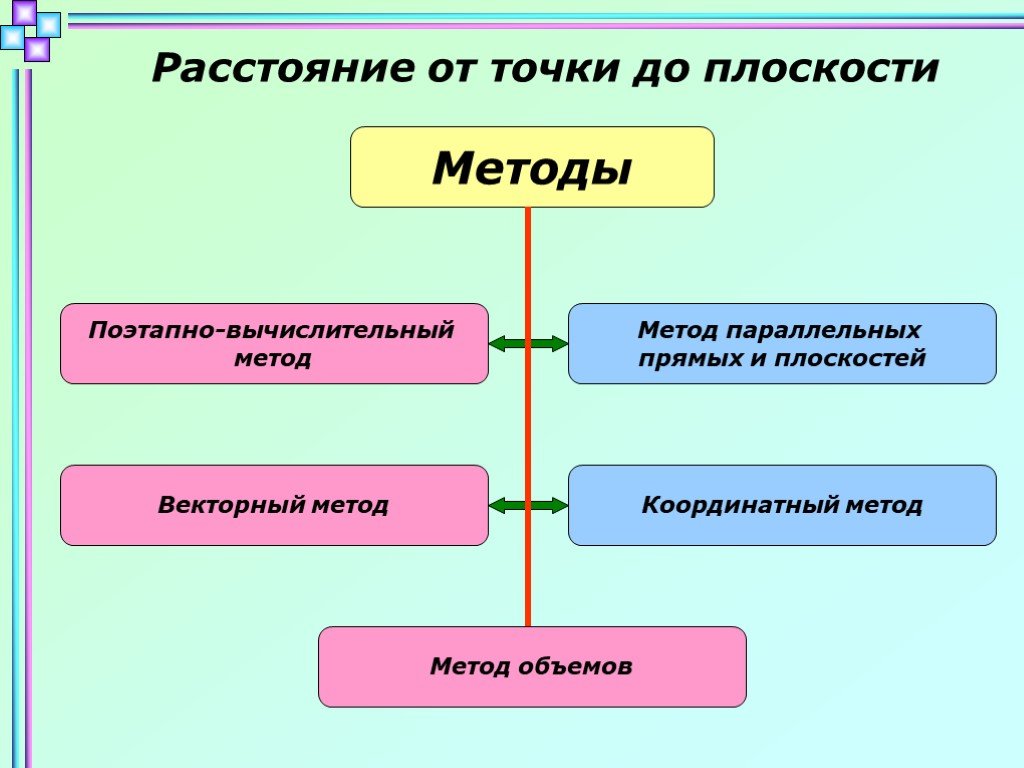
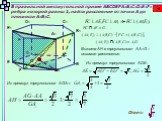
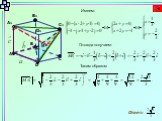
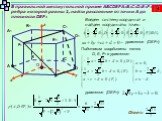
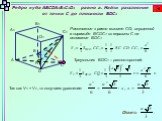
Презентация "Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости)" по математике – проект, доклад
Презентацию на тему "Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости)" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 8 слайд(ов).
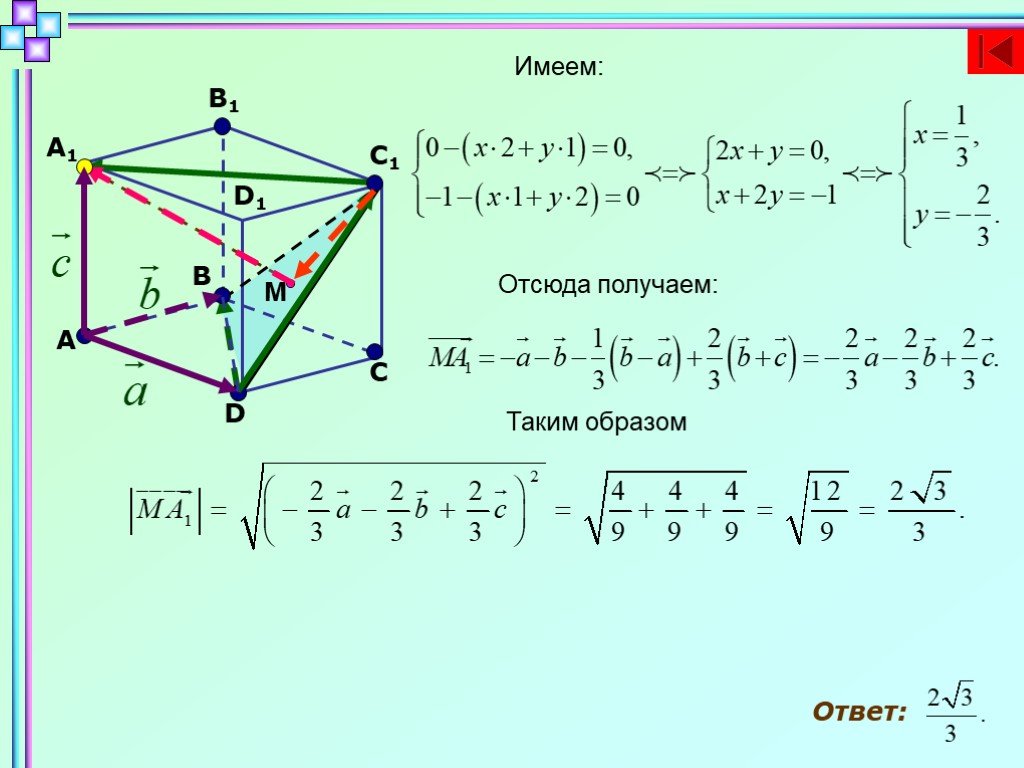
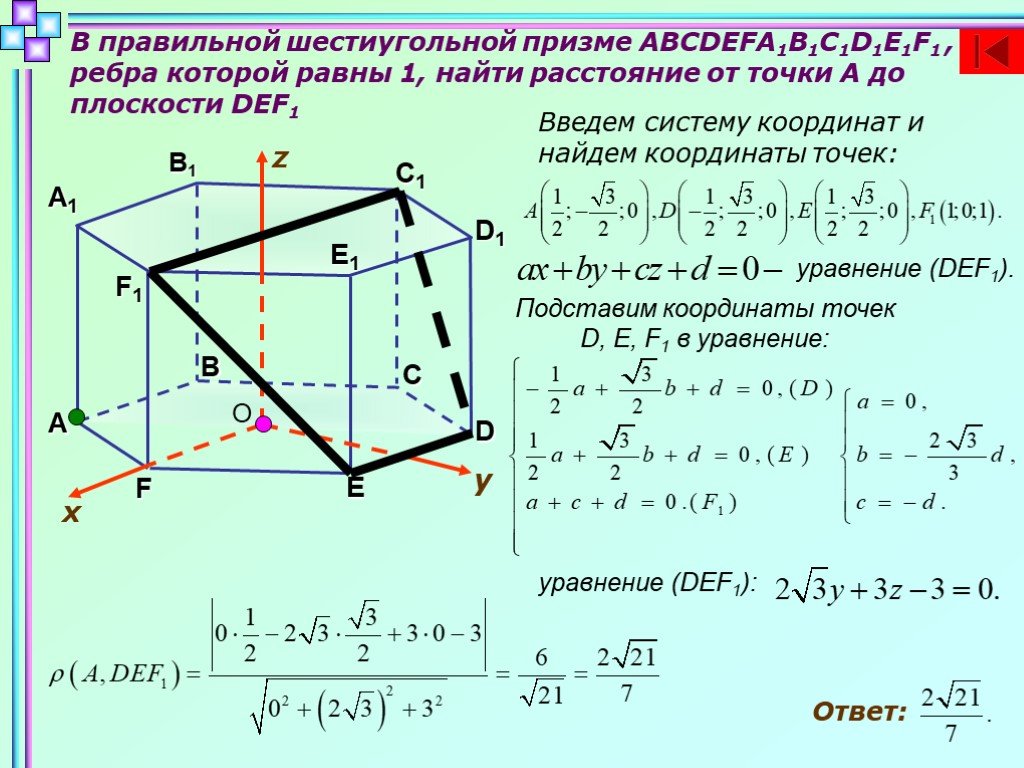
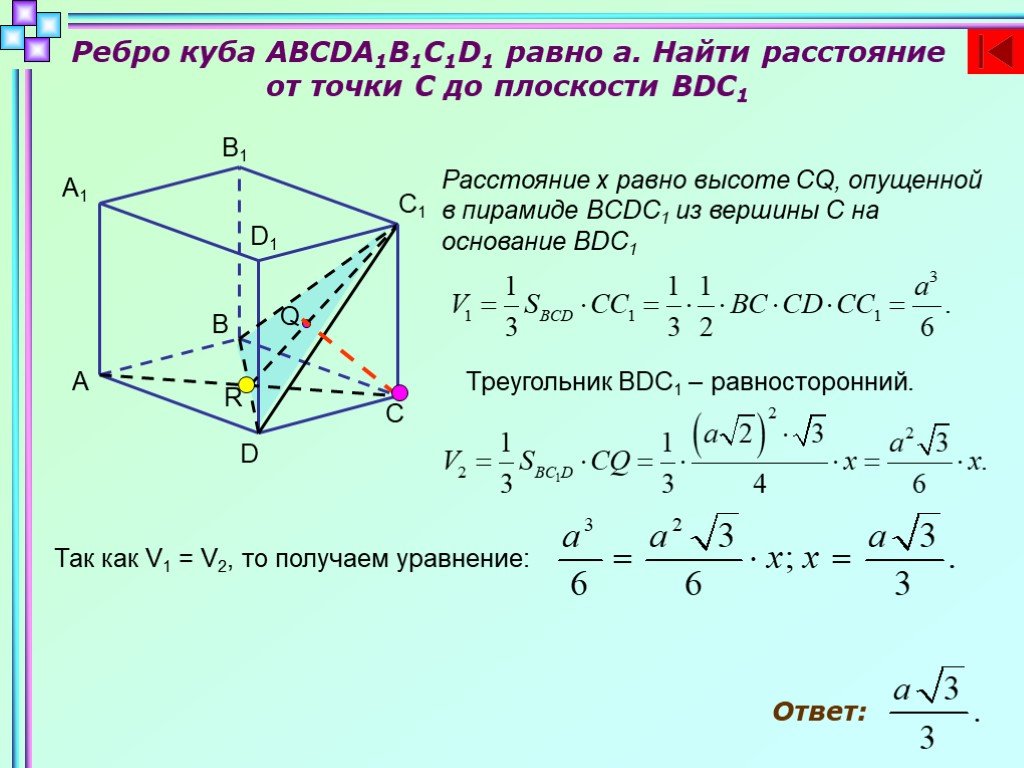
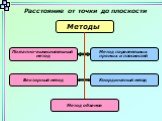
Слайды презентации
Список похожих презентаций
Биографии великих математиков (от сотворения мира до наших дней)
Фалес Милетский (ок. 625–547 гг. до н.э.). Греческий купец, живший в Милете, греческом полисе (городе-государстве на западном побережье Малой Азии; ...Готовимся к ЕГЭ
Практико-ориентированные задачи В1. 1. В доме, в котором живёт Петя , 9 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Петя ...Готовимся к ЕГЭ
Шоколадка стоит 31 рубль. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну ...Графические приемы решения задач с параметрами
Решение уравнений и неравенств, содержащих параметры, является одним из самых трудных разделов элементарной математики. Для их решения обычно требуются ...Готовимся к ЕГЭ
До снижения цен футболка стоила 1200 руб., а после снижения цен стала стоить 960 руб. На сколько процентов была снижена цена? В1 Ответ: 20. В2. Определите ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Геометрия до Евклида в очерках и задачах
Введение:. Цель моей работы: Изучение исторических сведений, показать связь основных этапов развития математики с этапами развития человечества. Задачи ...Аналитические методы решения логарифмических уравнений
Цели урока:. Обобщить и систематизировать изученные методы решения логарифмических уравнений Выявить особенности каждого метода Выяснить, всегда ли ...Аналитический и численный методы решения систем уравнений с параметром
АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...Алгоритмы работы на координатной плоскости
Цели:. Формировать умение работать на координатной плоскости как с положительными, так и отрицательными координатами. Развивать алгоритмическое мышление. ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Геометрические фигуры на плоскости
Цели урока. Вспомнить изученные геометрические фигуры и их свойства Убедиться в том, что геометрия не просто школьный предмет, а наука, на которой ...Геометрические задания группы В ЕГЭ
Задания группы В4. 1. В треугольнике АВС угол С равен 90°, sin A = 1/7, AC = 4√3. Найдите AB. B A 4√3 C Ответ: 7. 2. В треугольнике АВС угол С равен ...Вычитание. Решение задач с помощью действия вычитания
Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...Аксиомы расположения точек на прямой и плоскости
Выполните действия и сделайте записи:. 1. Изобразите точку С, лежащую на прямой а. 2. Изобразите точку D, не лежащую на этой прямой. 3. Проведите ...Декартовы координаты на плоскости
Я мыслю – следовательно, я существую. Рене Декарт Фото с сайта http://pimno.vspu.ru/Prodject/navigator/People/Dekart_Rene.htm. Отметьте точки A (1; ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Графический метод решения систем уравнений с двумя переменными
Обобщить графический способ решения систем уравнений; Сформировать умения графи-чески решать системы уравне-ний второй степени, привлекая известные ...Конспекты
Задача. Нахождение и запись решения
План – конспект урока. «Задача. Нахождение и запись решения». 1. ФИО (полностью). . Попова Марина Викторовна. . 2. . Место работы. ...Задачи на нахождение процента от величины
Тема урока: «Задачи на нахождение процента от величины». Цель урока:. . . Р. асширить и углубить знания учащихся о решении задач на проценты. ...Задача. Нахождение и запись решения
Букина Надежда Степановна. Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 8». Конспект урока по математике: ...Животноводство в нашем крае. Решение задач на движение
Муниципальное общеобразовательное учреждение. «Туендатская основная общеобразовательная школа». Первомайского района Томской области. ...Время от 0 часов до 24 часов
Математика 4 класс. УМК «Школа России». . . Конспект подготовила учитель начальных классов МБОУ «СОШ №33 г.Владимира». Королёва Любовь Петровна. ...Виды уравнений. Методы решения уравнений
ГАОУ НПО Профессиональный лицей № 59. Оренбургская область, Красногвардейский район, с. Плешаново. Виды уравнений. Методы решения уравнений. ...Жизнь диких животных зимой. Решение задач
Название работы. : Интегрированный урок математика + окружающий мир по теме: «Жизнь диких животных зимой. Решение задач. » . . Автор:. Валеева ...Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Геометрическое решение негеометрических задач
Урок по теме:. «Геометрическое решение негеометрических задач». Сивак Светлана Олеговна. учитель математики. высшей категории. Гимназии №56. ...Дополнение условия задачи. Решение задач
Конспект урока по математике для 1 класса по УМК 21 век. ТЕМА. :. «Дополнение условия задачи. Решение задач». ЦЕЛИ:. 1. Учить выделять части задачи, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 апреля 2019
Категория:Математика
Содержит:8 слайд(ов)
Поделись с друзьями:
Скачать презентацию