Презентация "Как находить площадь многоугольника" по математике – проект, доклад
Презентацию на тему "Как находить площадь многоугольника" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
Как находить объём прямоугольного параллелепипеда
"Предмет математики настолько серьезен, что полезно не упускать случая делать его не- много занима- тельным". Блез Паскаль. Геометрические тела и ...Деловая игра "Строитель"" к уроку математики по теме "Площадь многоугольника"
Цель урока:. усвоение учащимися формул для вычисления площадей параллелограмма, треугольника, трапеции применение полученных знаний к решению практических ...Площадь многоугольника
Как и другие науки, математика возникла из практических нужд людей: из измерения площадей земельных участков и вместимости сосудов, из счисления времени ...Площадь многоугольника
разминка з а д а н и е 1. 1 3 5 6 4 8 7. Запишите правильную последовательность цифр. Правильно, если: 6,5.3,1,4,7,8,2. разминка з а д а н и е 2. ...Площадь многоугольника
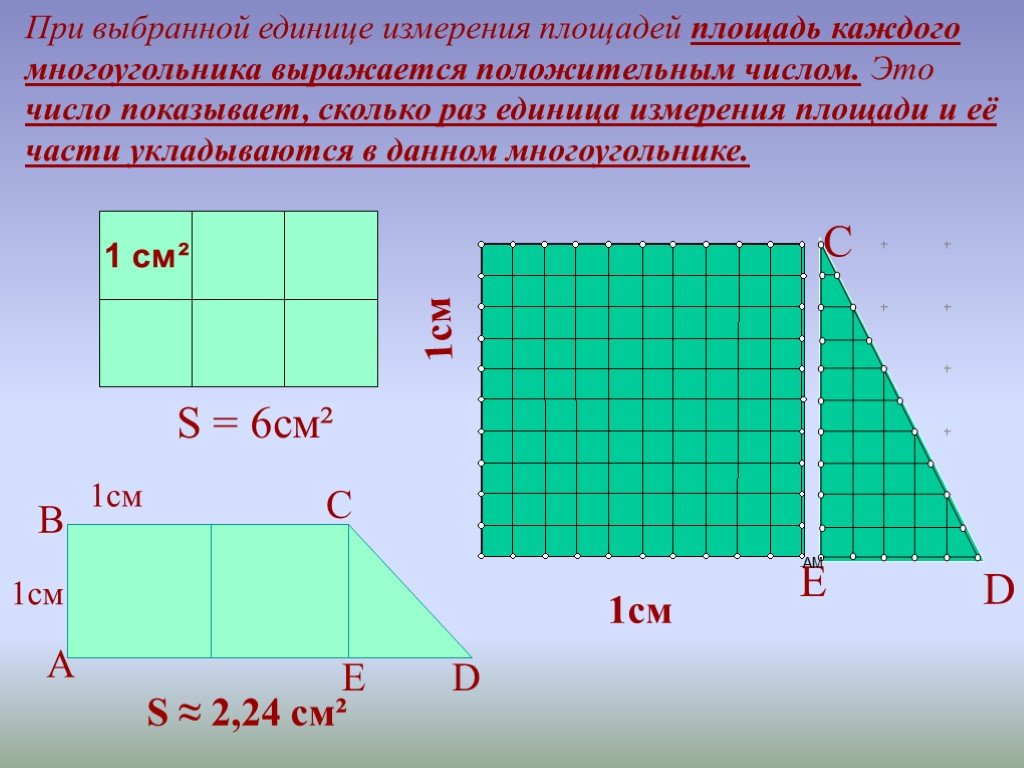
Цели урока:. Получить представление об измерении площадей многоугольника; Основные свойства площадей; Вывод формулы для вычисления площади квадрата; ...Площадь многоугольника"
Площадь треугольника. Площадь треугольника знали предки те, что пол основания брать по высоте. Формула Герона. Герон полупериметр под корень затащил, ...Как найти площадь прямоугольника?
. «Тот , кто не знает математики, не может изучить другие науки и не может познать мир». Роджер Бекон. Зарядка для ума. На какие группы можно разделить ...Площадь многоугольника
Свойства фигур Задачи II уровня Задачи I уровня Формулы Тесты I уровня Тесты II уровня Это интересно. . Вопрос 1. Найти площадь треугольника, если ...Как построить симметричную фигуру
Урок технологии Урок информатики. «Раз стоя перед чёрной доской и рисуя мелом разные фигуры я вдруг был поражён мыслью: почему симметрия приятна для ...Длина окружности и площадь круга
Назовите: а) окружность, б) круг. 1) 2) 4) 5) 6) 7). Дайте названия линиям и точкам Какой формулой связаны радиус и диаметр? ??? окружность центр ...Как построить график функции y=f(x+L)+m, если известен график функции y=f(x)
ТЕМА УРОКА Как построить график функции y=f(x+L)+m, если известен график функции y=f (x). Цель урока: Научиться строить график функции y=f (x + L) ...Определение многоугольника
Предмет : математика Элективный курс «Избранные задачи и теоремы планиметрии» Класс: 9 Тема урока: “Многоугольники (Заключительный урок по теме)” ...Как возникли дроби
Роман Корженевский, 5 класс. Слыхали ли Вы о том, как ломают числа? А ведь ломаными числами пользуются и теперь, только называют их иначе. Попробуйте ...Как чётная и нечётная степень влияет на знак числа
Цель: Научиться возводить отрицательное число в степень. Задачи: Выучить правило возведения числа в степень. Научиться применять это правило для решения ...Найти площадь криволинейной трапеции
Определение производной:. Найти производную функции по определению:. Вставьте вместо *. Определение первообразной:. Будут ли первообразными следующие ...Как доказать истину в геометрии?
Как доказать истину в геометрии? Авторы: учащиеся 7Д класса МОУ «Средняя общеобразовательная школа №2 города Кувандыка Оренбургской области». Цель ...Как записываются десятичные дроби
Цель урока:. Закрепить навыки в умении записывать десятичные дроби. Стимулировать развитию разнообразной творческой деятельности. Способствовать воспитанию ...Как готовиться к ГИА-9 по математике
. Содержание работы. Всего в работе 26 заданий, из которых 20 заданий базового уровня (часть I) и 6 заданий повышенного уровня (часть II). Работа ...Как готовиться к ЕГЭ по математике
Задача С1. 1) Считать «картинку» необходимой частью решения тригонометрического уравнения (даже, если отбор корней не нужен). Не употреблять запись ...Как выполняли арифметические действия в Древнем Риме?
узнать как выполнялись арифметические действия в Древнем Риме. Цель:. Актуальность: Я считаю необходимым проведение этого исследования, так как: Я ...Конспекты
Площадь и периметр многоугольника
Горкунова Вера Юрьевна МОУ «Гимназия» г. Чернушка, Пермский край. . Конкурсный урок. Математика. Тема:. Модель и способ. Повторение знаний по ...Площадь многоугольника
Автор: Чичерова Татьяна Ивановна. Место работы: МОУ «Образцовская СОШ». Должность: учитель математики. . . Урок геометрии в 8классе. Тема: ...Периметр многоугольника
Урок математики. . 2 класс. Тема урока: Периметр многоугольника. Тип урока:. урок открытия нового знания. . Деятельностная цель:. формирование ...Периметр многоугольника
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа №24. Конспект урока по математике. . «Периметр ...Периметр многоугольника
Технологическая карта урока математики. по теме: «Периметр многоугольника» в рамках ФГОС. . Ф.И.О. педагога: Никитина Светлана Геннадьевна. ...Периметр многоугольника
Конспект урока по курсу “Математика» 2 класс. УМК:. «Школа России». Учитель: Бурова К. В. ГБОУ СШ №365. Тема урока:. . «Периметр многоугольника». ...Периметр многоугольника
Технологическая карта урока математики по теме «Периметр многоугольника». Учитель математики Чумичева Ирина Борисовна. Класс: 5. Тема урока: периметр ...Вычисляем площадь
ТЕМА УРОКА:. Вычисляем площадь. Цель:. создать учебную ситуацию для поиска различных способов нахождения площади прямоугольника. Задачи:. ...Объем и площадь поверхности конических тел
Урок 4. Тема урока: «Объем и площадь поверхности конических тел». Тип учебного занятия:. изучение и первичное закрепление новых знаний и способов ...Длина окружности и площадь круга
Автор Козлова Елена Юрьевна. Учитель математики. Тема урока «Длина окружности и площадь круга». Учебно-методическое обеспечение:. учебник Математика, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:21 марта 2019
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию







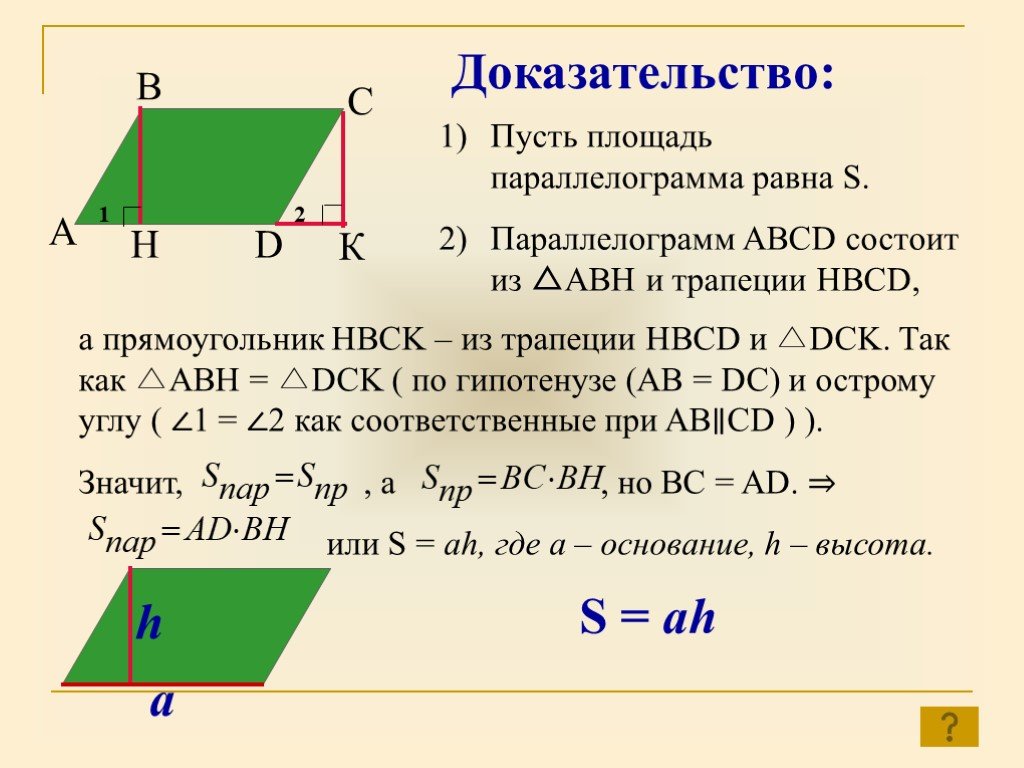
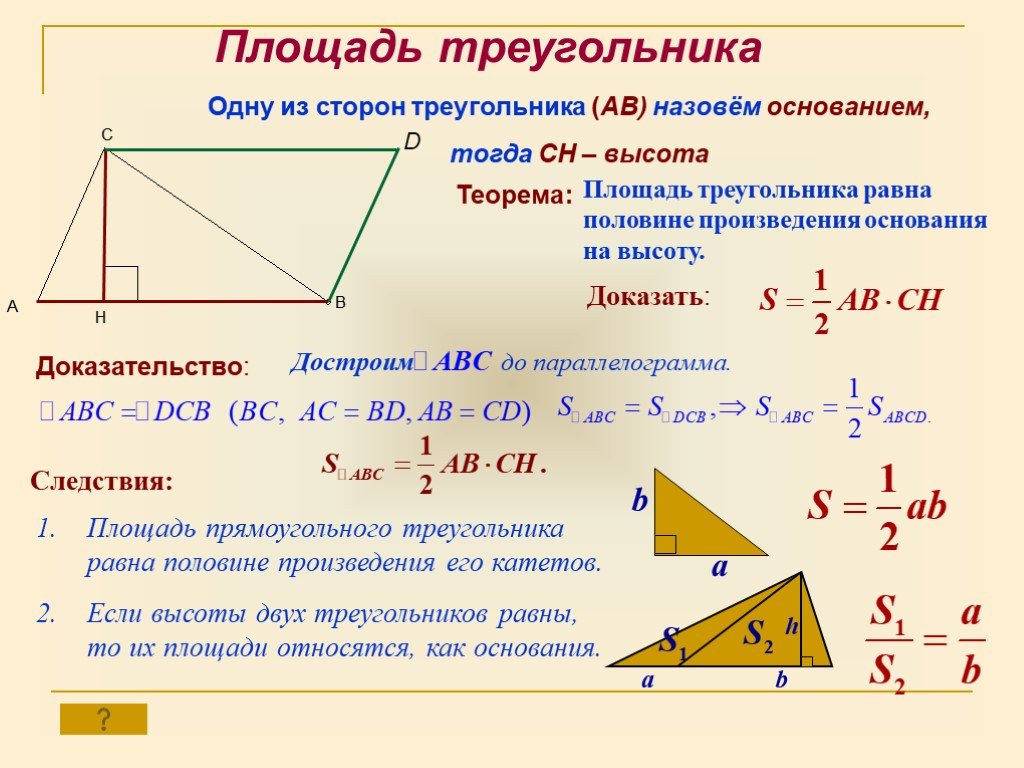








![Все мы понимаем смысл слов: площадь комнаты равна 25 м² , площадь сада – 6 соткам.С понятием «площадь» и формулами для вычисления площадей некоторых фигур вы уже встречались. Какие это фигуры? [ прямоугольник: S = ab; круг: S= ]. Площадь поверхности стен в помещении нужно знать, например, для того, Все мы понимаем смысл слов: площадь комнаты равна 25 м² , площадь сада – 6 соткам.С понятием «площадь» и формулами для вычисления площадей некоторых фигур вы уже встречались. Какие это фигуры? [ прямоугольник: S = ab; круг: S= ]. Площадь поверхности стен в помещении нужно знать, например, для того,](https://prezentacii.org/upload/cloud/19/03/135438/images/thumbs/screen6.jpg)


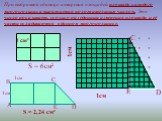




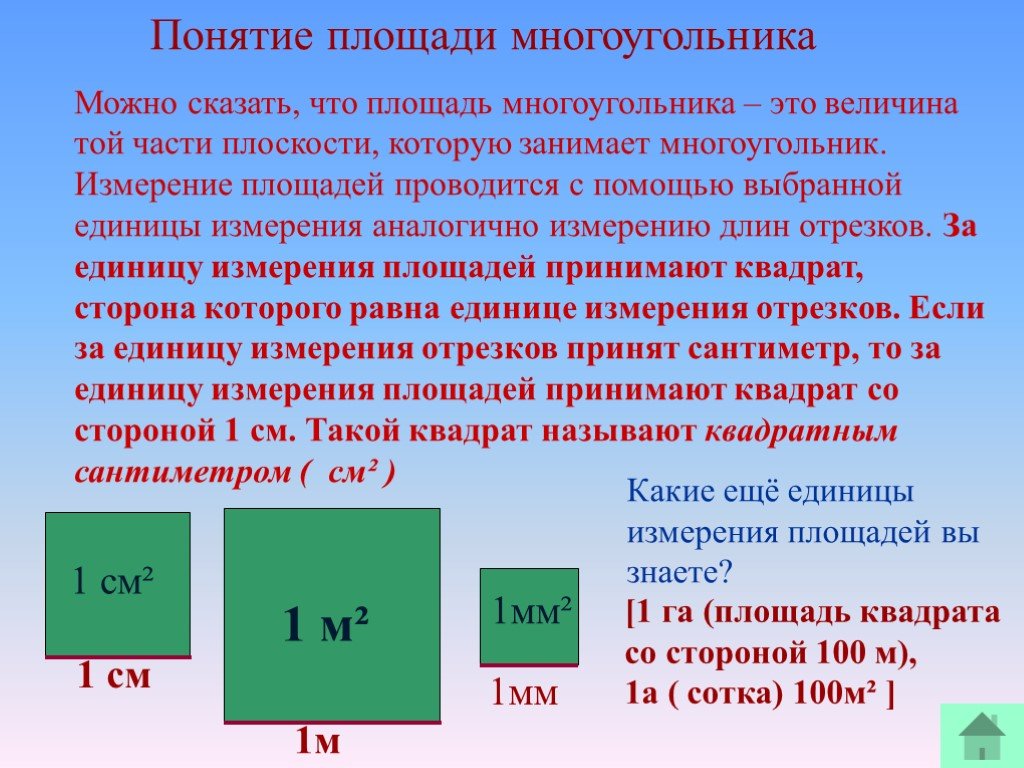
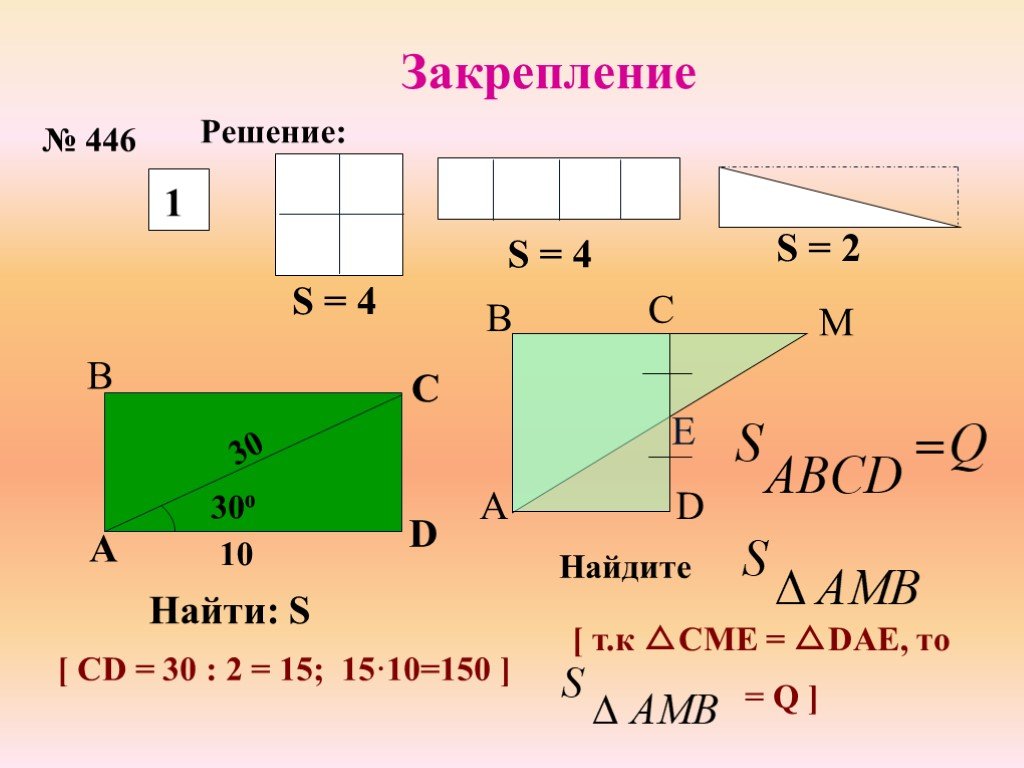
![Закрепление № 446 Решение: S = 4 S = 2 30 30⁰ 10 Найти: S [ CD = 30 : 2 = 15; 15·10=150 ] Найдите [ т.к △СМЕ = △DAE, то = Q ] E Закрепление № 446 Решение: S = 4 S = 2 30 30⁰ 10 Найти: S [ CD = 30 : 2 = 15; 15·10=150 ] Найдите [ т.к △СМЕ = △DAE, то = Q ] E](https://prezentacii.org/upload/cloud/19/03/135438/images/thumbs/screen15.jpg)