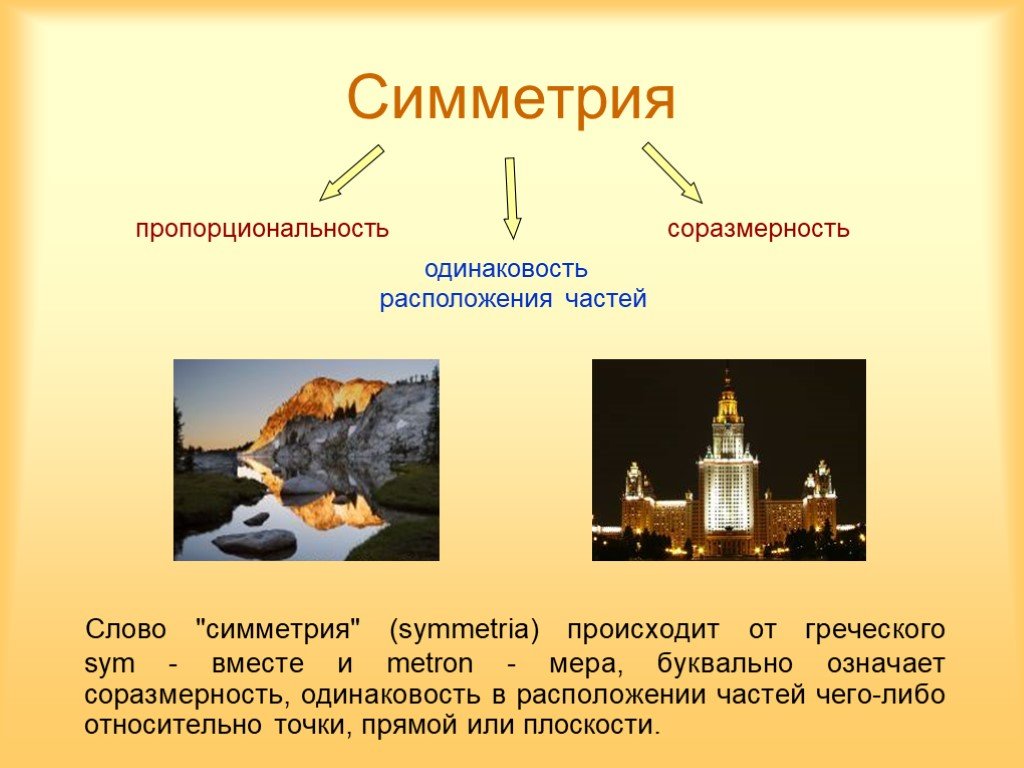
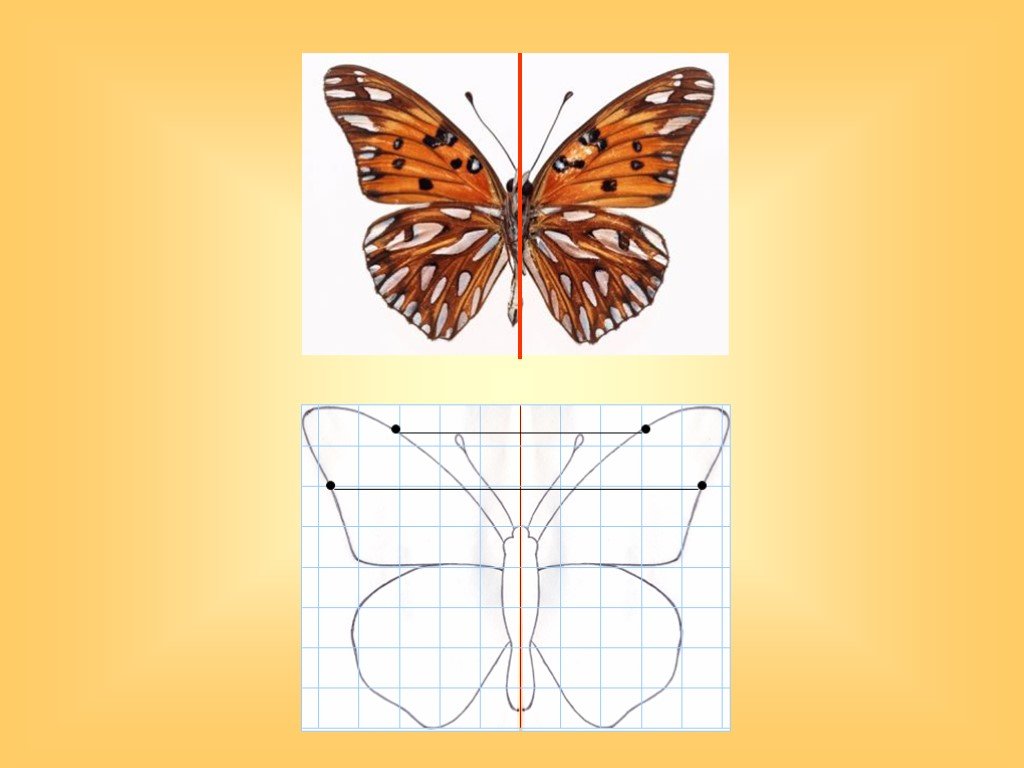
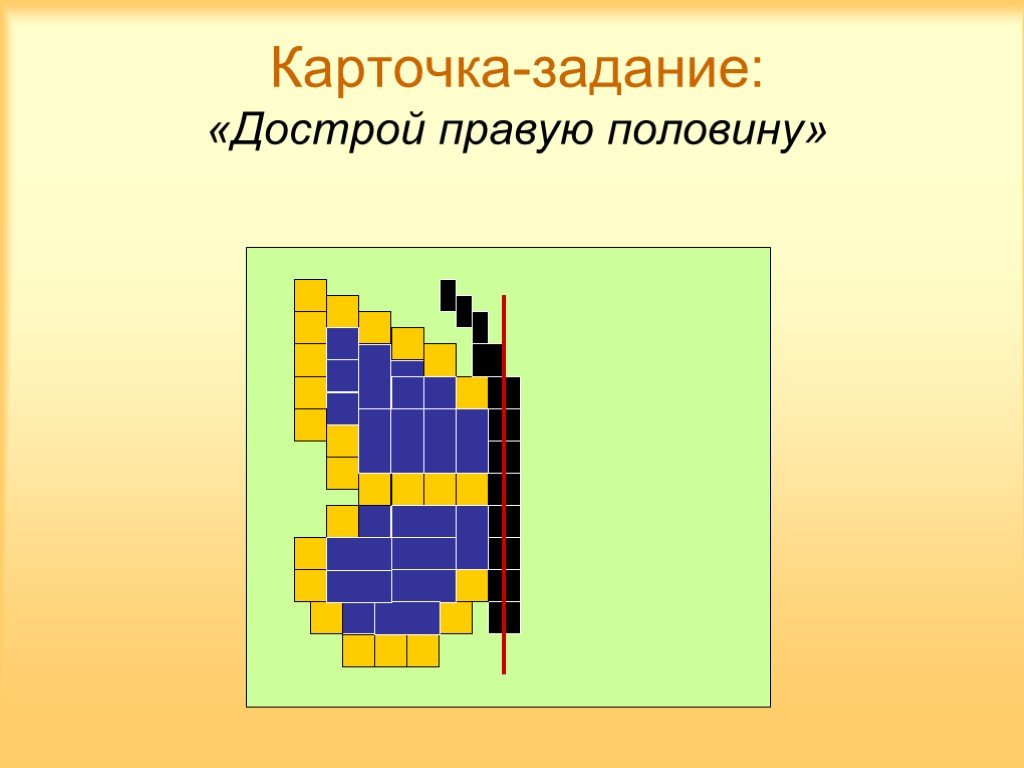
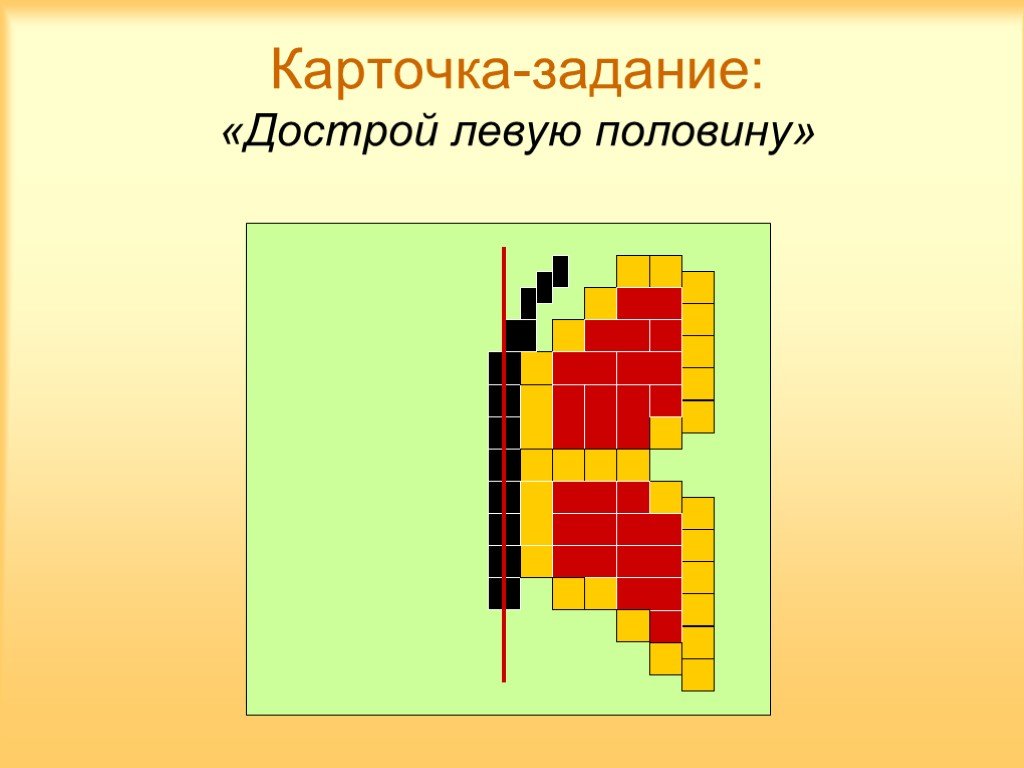
Презентация "Как построить симметричную фигуру" по математике – проект, доклад

Скачать презентацию (2.21 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Презентацию на тему "Как построить симметричную фигуру" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).

Скачать презентацию (2.21 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Департамент образования города Москвы Западное окружное управление образования района Филёвский парк

Из опыта работы Центра развивающих игр (ЛЕГОТЕКИ) Руководитель леготеки: учитель технологии – Перцева Оксана Валерьевна

ГОУ ЦО №1497

Слайд 2

Урок технологии Урок информатики

«Раз стоя перед чёрной доской и рисуя мелом разные фигуры я вдруг был поражён мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врождённое чувство, отвечал я сам себе. На чём оно основано? Разве во всём в жизни симметрия?» Л. Толстой «Отрочество»

Урок ИЗО

Слайд 3

Разве во всём в жизни симметрия? Действительно, стоит оглянуться вокруг, чтобы убедиться , что это так: рыбы и птицы, животные и насекомые, обезьяна и человек, цветы и листья , грибы и водоросли – во всём в жизни симметрия!

Слайд 4

Тема: «Симметрия. Технологические приёмы конструирования симметричных фигур.»

Цель урока: научить строить симметричные точки и распознавать фигуры, обладающие симметрией; способствовать развитию логического мышления и познавательной активности учащихся; научиться применять законы симметрии в творческих работах по леготехнологии. Оборудование: наборы ЛЕГО. Зрительный ряд: видео сопровождение, технологические карты. ТСО: компьютер, мультимедийный проектор.

Слайд 5

Содержание урока

Понятие симметрии Симметрия в природе Симметрия в архитектуре Орнаменты Технологические приёмы конструирования: - плоскостное конструирование; - вертикальное конструирование; - объёмное конструирование

Слайд 6

Симметрия

Слово "симметрия" (symmetria) происходит от греческого sym - вместе и metron - мера, буквально означает соразмерность, одинаковость в расположении частей чего-либо относительно точки, прямой или плоскости.

пропорциональность

соразмерность

одинаковость расположения частей

Слайд 7

«Надо учиться у самой природы, которая сама по себе есть замечательный сад гармонии». Леонардо да Винчи

Представитель эпохи Возрождения - гениальный живописец, ученый и инженер Леонардо да Винчи (1452-1519)

Первоначальное понятие о геометрической симметрии как о соразмерности частей целого, как о гармонии пропорций целого с течением времени приобрело универсальный смысл.

Слайд 8

Симметрия в природе

Различные виды симметрии определяют гармонию. Почти все живые существа построены по законам симметрии, ведь недаром в переводе с греческого слово «симметрия» означает «соразмерность».

Симметрия воспринимается человеком, как проявление закономерности , порядка царящего в природе.

Слайд 9

Симметрия в архитектуре

Здание Парфенона

Человек издавна использовал симметрию в архитектуре. Старинным дворцам и современным зданиям она придает законченный гармоничный вид.

Триумфальная арка

«Красота тесно связана с симметрией». Максвелл Д.

Слайд 10

Орнамент

Орнаменты с давних времён украшают памятники архитектуры. Мы любуемся орнаментом потому что видим не только краски, но и симметрично повторяющиеся узоры, комбинации простейших геометрических фигур, лежащих в основе орнамента.

Слайд 11

Восстановление орнамента

Восстановление памятников архитектуры и искусства важная задача, стоящая перед нашим поколением. При реставрации пострадавших от времени орнаментов, изображённых в настенных узорах , на коврах или на решётках, нынешние умельцы с помощью законов симметрии разгадывают геометрическую основу, используемую древними резчиками и ткачами.

Слайд 13

Карточка-задание: «Дострой правую половину»

Слайд 14

Карточка-задание: «Дострой левую половину»

Слайд 15

Виды конструирования

Плоскостное конструирование Вертикальное конструирование Объёмное конструирование

Слайд 16

Вертикальное конструирование

Плоскостное конструирование

Объёмное конструирование

Слайд 17

Технологическая карта. Плоскостное конструирование «Бабочка»

1х2 – 6 шт. 2х2 – 8 шт. 2х4 – 1 шт. 2х2 – 6 шт. 2х4 - 26 шт. 2х2 – 44 шт.

ГОУ ЦО №1497 ЗОУОДО г. Москвы

Автор: Перцева О. В.

Слайд 18

2х4 – 5 шт. 1х2 – 2 шт. 2х2 – 22 шт. 2х2 – 10 шт.

Слайд 19

Технологическая карта. Вертикальное конструирование «Бабочка»

2х2 – 13 шт. 2х4 – 2 шт. 2х2 – 4 шт. 2х2 - 18 шт. 2х3 – 12 шт. 2х4 – 8 шт.

Слайд 20

Технологическая карта. Объёмное конструирование «Бабочка»

Туловище: 6 кирпичиков - на 2х4

Крыло: ступенчатое соединение 4 кирпичика – 2х4 6 кирпичиков – 2х2

Усы: 2 кирпичика – 1х6

Слайд 22

В презентации использованы работы учащихся 3-х классов

Список похожих презентаций

Как построить график функции y=f(x+l)+m из графика функции y=f(x)

x y 1 0 6 3. Устная работа на повторение. 1) [-1;3] 2) [0;6] 3) [-2;6] 4) [0;3]. Найдите область определения функции. -2. Найдите область значений ...

Как построить график функции у = mf(x),если известен график функции у = f(x)

Вид преобразования: параллельный перенос. у = х у = 2х у =½х. у = 4х у =¼х. у =½x² у =2 х². у=5х² у = х². что произойдет с графиками при умножении ...

Как построить график функции y=f(x+L)+m, если известен график функции y=f(x)

ТЕМА УРОКА Как построить график функции y=f(x+L)+m, если известен график функции y=f (x). Цель урока: Научиться строить график функции y=f (x + L) ...

Как считали в древности

Первобытные народы считают. Числа получают имена. Операции над числами. Древняя Греция Древний Рим. Шумерская клинопись. Древний Египет Вавилония ...

Как возникли цифры?

Цель работы:. Выяснить, когда и как возникли цифры, распознать различные системы счета. В древние времена, когда человек хотел показать сколькими ...

Как повысить качество знаний на уроках математики?

Предмет математики настолько серьёзен, что полезно не упускать случаев делать его немного занимательным. ( Б.Паскаль.). Главная задача каждого преподавателя: ...

Как находить объём прямоугольного параллелепипеда

"Предмет математики настолько серьезен, что полезно не упускать случая делать его не- много занима- тельным". Блез Паскаль. Геометрические тела и ...

Как найти площадь прямоугольника?

. «Тот , кто не знает математики, не может изучить другие науки и не может познать мир». Роджер Бекон. Зарядка для ума. На какие группы можно разделить ...

Как найти длину окружности

Половина длины окружности единичного радиуса обозначается греческой буквой π. Таким образом, длина окружности единичного радиуса равна 2π. Из рассмотренной ...

Как возникли дроби

Роман Корженевский, 5 класс. Слыхали ли Вы о том, как ломают числа? А ведь ломаными числами пользуются и теперь, только называют их иначе. Попробуйте ...

Как из двух врагов может получиться друг?

Цель: Научиться выполнять умножение и деление чисел с разными знаками. Задачи: Выучить правило умножения и деления чисел с разными знаками. Уметь ...

Как записываются десятичные дроби

Цель урока:. Закрепить навыки в умении записывать десятичные дроби. Стимулировать развитию разнообразной творческой деятельности. Способствовать воспитанию ...

Как доказать истину в геометрии?

Как доказать истину в геометрии? Авторы: учащиеся 7Д класса МОУ «Средняя общеобразовательная школа №2 города Кувандыка Оренбургской области». Цель ...

Как готовиться к ЕГЭ по математике

Задача С1. 1) Считать «картинку» необходимой частью решения тригонометрического уравнения (даже, если отбор корней не нужен). Не употреблять запись ...

Как готовиться к ГИА-9 по математике

. Содержание работы. Всего в работе 26 заданий, из которых 20 заданий базового уровня (часть I) и 6 заданий повышенного уровня (часть II). Работа ...

Как выполняли арифметические действия в Древнем Риме?

узнать как выполнялись арифметические действия в Древнем Риме. Цель:. Актуальность: Я считаю необходимым проведение этого исследования, так как: Я ...

Как учились математике дети в прошлые времена

Введение. Мне стало интересно: как учились дети математике в прошлом. Какие они решали задачи? Смогу ли я их решить? Будет ли мне трудно это сделать ...

Как читать графики

Как читать графики? Посев семян тыквы рекомендуется проводить в мае при дневной температуре воздуха не менее ° С. На рисунке показан прогноз ...

Как извлечь корень?

Подобрать число, квадрат которого ближе всего к 8. Отделить по две цифры справа налево. Это 2, т.к. 32=9. удвоить. Подобрать две одинаковые цифры ...

Как называются эти фигуры?

Как можно называть эту фигуру ? Четырёхугольник Многоугольник Квадрат Прямоугольник . Что такое квадрат ? Квадрат – это прямоугольник у которого ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.