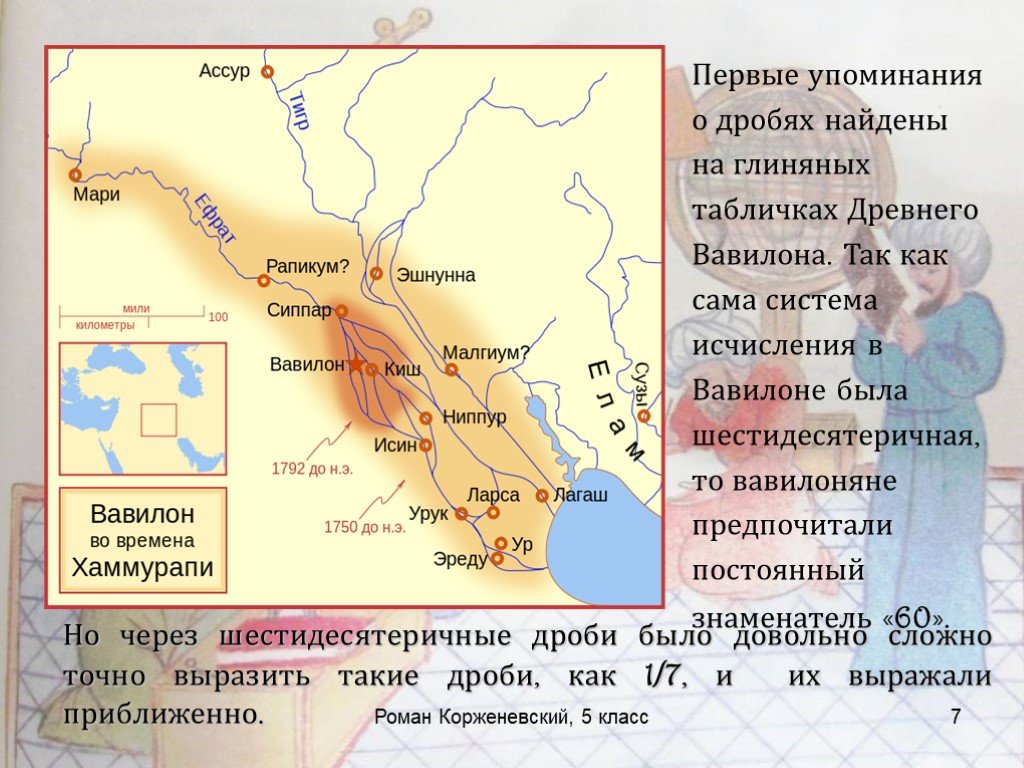
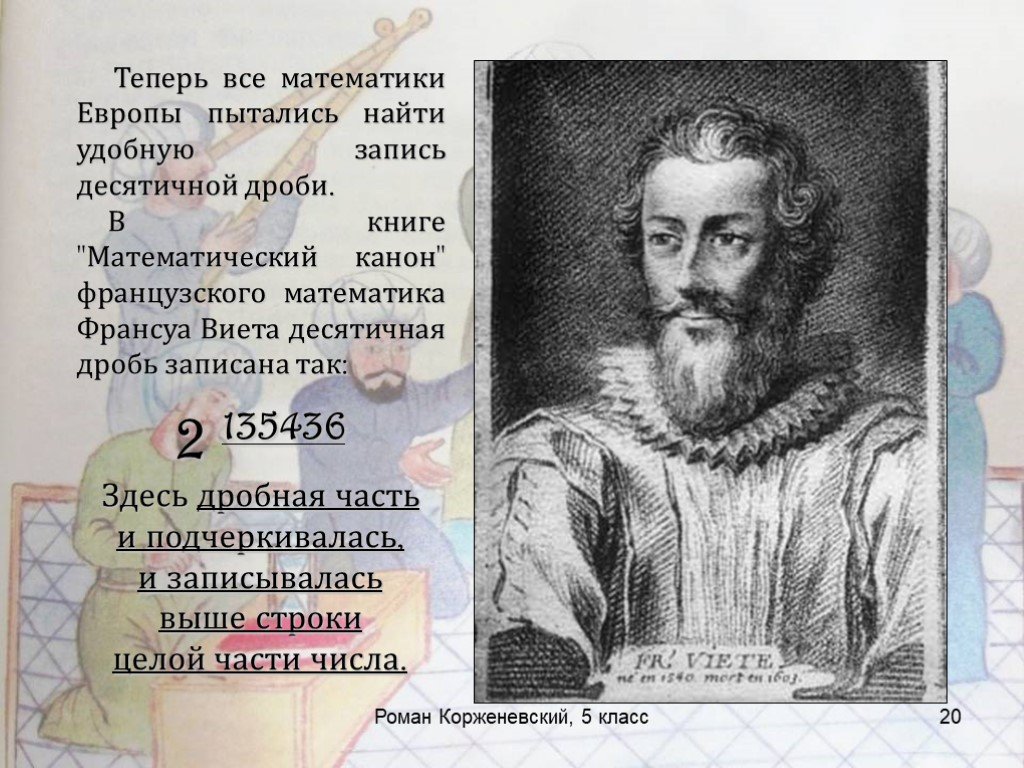
Презентация "Как возникли дроби" по математике – проект, доклад
Презентацию на тему "Как возникли дроби" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
Как возникли дроби?
«Историки». ПРЕДСТАВЛЯЮТ!!!!! «Как возникли дроби». В каких источниках впервые упоминается о дробях:. Египетский математический кожаный свиток Московский ...Как возникли цифры?
Цель работы:. Выяснить, когда и как возникли цифры, распознать различные системы счета. В древние времена, когда человек хотел показать сколькими ...Как записываются десятичные дроби
Цель урока:. Закрепить навыки в умении записывать десятичные дроби. Стимулировать развитию разнообразной творческой деятельности. Способствовать воспитанию ...Обыкновенные дроби
Обыкновенные дроби. Урок математики в 5 классе. Подготовила учитель математики МОУ «Ломовская СОШ» О.М.Якушева. Дроби всякие нужны, Дроби всякие важны. ...Обыкновенные дроби с одинаковыми знаменателями
Первое условие, которое надлежит выполнять в математике, - это быть точным, второе - быть ясным и, насколько можно, простым. Л. Карно. Рекомендации ...Нахождение дроби от числа и числа по его дроби
I.Прочитай задачи, запиши краткое условие, реши задачи. II.Cоставь свою стратегию решения задач. 1.Масса вяленой рыбы составляет 55% массы свежей ...Обыкновенные дроби
Цели урока:. Образовательные: обобщение знаний по теме: «Обыкновенные дроби». Воспитательные: воспитание аккуратности, дисциплины, настойчивости, ...Как решать неполные квадратные уравнения
Тема урока: Решение неполных квадратных уравнений. Покупка билетов. Вариант – 1. Решить уравнение:. Вариант – 2. Решить уравнение:. Устная работа. ...Конструирование системы задач в 5 классе по теме: "Задачи на дроби"
Цель проекта: «Исследовать методику работы над текстовой задачей, выявить новые подходы к решению текстовых арифметических задач, в частности задач ...Гарфилд изучает дроби
Программа позволяет учащимся усвоить основные понятия, связанные с определением обыкновенных дробей; научиться выполнять основные действия на дроби: ...Как находить объём прямоугольного параллелепипеда
"Предмет математики настолько серьезен, что полезно не упускать случая делать его не- много занима- тельным". Блез Паскаль. Геометрические тела и ...Аліквотні дроби
Первые дроби, с которыми нас знакомит история, это дроби вида –. – так называемые единичные дроби или аликвотные. Египетская дробь — в математике ...Арифметический квадратный корень из произведения и дроби
Он есть у дерева, цветка, он есть у уравнений,. 2х + 5 = 3 КОРЕНЬ. И знак особый – радикал, с ним связан, вне сомнений. Заданий многих он итог, и ...Алгебраические дроби Сокращение дробей
Проверка домашнего задания. № 434 № 435 № 436 №437. Алгебраические дроби. Алгебраическими называются дроби, в которых знаменатель и числитель представлены ...Алгебраические дроби с разными знаменателями
Повторить правила сложения и вычитания числовых дробей с разными знаменателями; Изучить правила сложения и вычитания алгебраических дробей с разными ...Алгебраические дроби
Алгебраическая дробь. Основные понятия Область допустимых значений Равенство дроби нулю. Многочлен сумма Одночлен. произведение чисел и степеней переменных ...Ох,уж эти дроби!
Можно ли измерить мир? В каких областях применяются большие единицы измерения? ( железная дорога, металлургия, космос , и т. д.) В каких областях ...Деление десятичной дроби на натуральное число
Мы отправляемся в экспедицию! Работают три научно-исследовательские лаборатории . Чтобы узнать куда мы отправляемся, надо устно решить примеры. Вычислите ...Правильные и неправильные дроби 5 кл
Цели урока:. Сегодня на уроке я хочу: Узнать…. Научиться….. Составлять…. Понять……. Сравнение дробей. С одинаковыми знаменателями С одинаковыми числителями ...Деление десятичной дроби на натуральное число
Это растение бергамот. Это цитрусовое растение. Плоды его несъедобны, но масло, которое получают из кожуры этих плодов, листьев и цветов, имеет приятный ...Конспекты
Приведение дроби к общему знаменателю
Тема урока: "Приведение дроби к общему знаменателю". Цель урока:. научиться приводить дроби к общему знаменателю. Задачи урока:. Образовательные. ...Решение задач на нахождение среднего арифметического нескольких чисел и на нахождение дроби от числа
ГКСОУ "Специальная (коррекционная) общеобразовательная школа - интернат VIII. вида г. Вязники". Урок по математике в 8 классе. «Решение ...Основное свойство дроби
Тема урока: Основное свойство дроби. Цели урока:. Образовательные:. . -. . ввести понятие основного свойства дроби;. . - учить применять основное ...Правильные и неправильные дроби
Тема урока. : «Правильные и неправильные дроби». Цели урока. :. Образовательная:. организовать деятельность учащихся по повторению и закреплению ...Обыкновенные дроби
ПЛАН-КОНСПЕКТ УРОКА Решение задач повышенной сложности по теме «Обыкновенные дроби». . ФИО (полностью). . Данилова Лидия Андреевна. . ...Обыкновенные дроби. Правильные и неправильные дроби
Методическая разработка урока проверки знаний. Урок математики в 5-м классе. Повторение по теме "Обыкновенные дроби. Правильные и неправильные дроби". ...Деление десятичной дроби на десятичную дробь
Технологическая карта. Математика.5 класс. Тема. «Деление десятичной дроби на десятичную дробь». . Тип урока. . Урок отработки умений ...Нахождение числа по значению дроби
Дата: 06. 12.13г. Математика 6 класс. Учитель: Луконина Н.Б. Урок – игра «Детективное агентство 304» с применением технологий системно - деятельностного ...Действия с обыкновенными дробями. Основные задачи на дроби
ГБС(К)ОУ ШИ. I. -. II. вида г. Тихорецка Краснодарского края. Урок – КВН. в 7 классе по теме:. «Действия с обыкновенными дробями. Основные ...Деление десятичной дроби на десятичную дробь
Учитель: Очирова Мидыгма Гомбоевна. Предмет: математика. Класс: 5. Тема урока: Деление десятичной дроби на десятичную дробь (1-ый урок). Цель ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 декабря 2018
Категория:Математика
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию