Презентация "Симметрия" по математике – проект, доклад

Симметрия

Работу выполнили: Александрин Илья Веретенников Антон Ханин Андрей Довлекаева Эльвира

Содержание

Симметрия в кристаллах Симметрия в архитектуре Симметрия в технике Симметрия в природе Заключение

Рассмотрим внимательно многогранные формы кристаллов. Прежде всего видно, что кристаллы разных веществ отличаются друг от друга по своим формам. Каменная соль - это всегда кубики; горный хрусталь - всегда шестигранные призмы, иногда с головками в виде трехгранных или шестигранных пирамид; алмаз - чаще всего правильные восьмигранники (октаэдры); лед - шестигранные призмочки, очень похожие на горный хрусталь, а снежинки - всегда шестилучевые звездочки. Что бросается в глаза, когда смотришь на кристаллы? Прежде всего, их симметрия.

Кристаллы

К понятию о симметрии мы привыкаем с детства. Мы знаем, что симметрична бабочка: у неё одинаковы правое и левое крылышки; симметрично колесо, секторы которого одинаковы; симметричны узоры орнаментов, звёздочки снежинок. Симметричными мы называем тела, которые состоят из равных, одинаковых частей. Эти части могут совмещаться друг с другом. Симметрия бывает разной. Какова, например, симметрия бабочки? Бабочка может сложить крылья, и тогда две её одинаковые половинки совмещаются. Это можно описать и иначе. Любое из двух крыльев бабочки как бы отражается в зеркале. Мы говорим, что половинки бабочки зеркально равны или что бабочка обладает плоскостью симметрии.

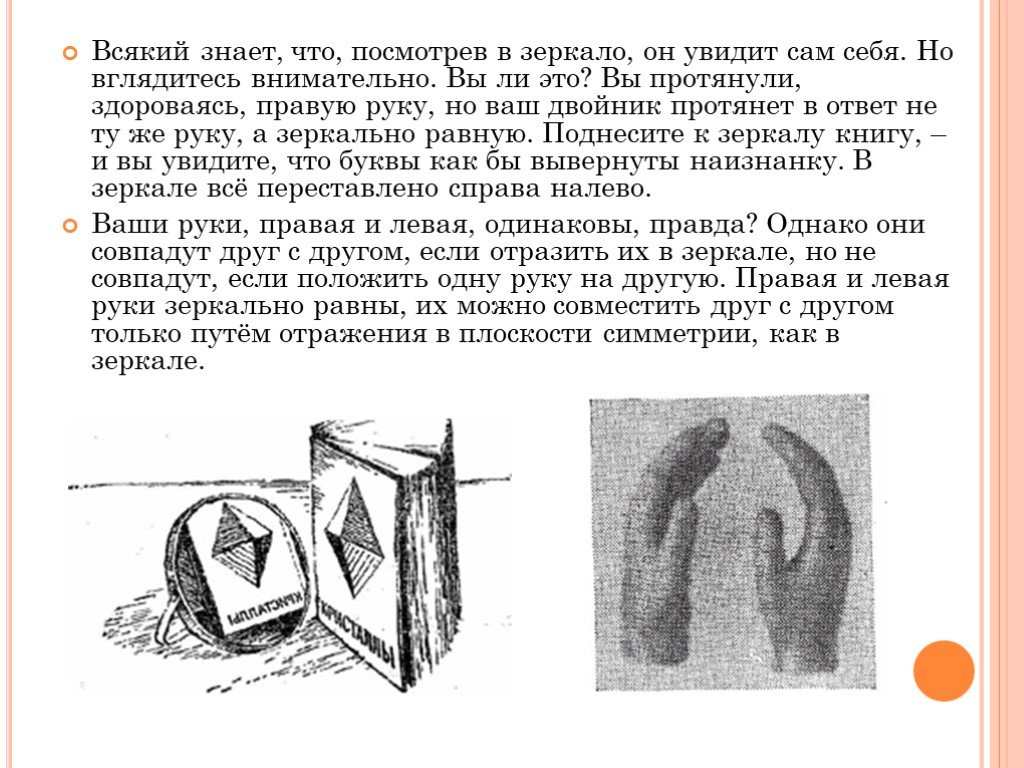
Всякий знает, что, посмотрев в зеркало, он увидит сам себя. Но вглядитесь внимательно. Вы ли это? Вы протянули, здороваясь, правую руку, но ваш двойник протянет в ответ не ту же руку, а зеркально равную. Поднесите к зеркалу книгу, – и вы увидите, что буквы как бы вывернуты наизнанку. В зеркале всё переставлено справа налево. Ваши руки, правая и левая, одинаковы, правда? Однако они совпадут друг с другом, если отразить их в зеркале, но не совпадут, если положить одну руку на другую. Правая и левая руки зеркально равны, их можно совместить друг с другом только путём отражения в плоскости симметрии, как в зеркале.

Плоскости симметрии можно обнаружить и в кристаллах. В снежинке, например, можно найти даже не одну плоскость симметрии, а шесть. Представьте себе, что снежинка отражается в любом из зеркал, следы которых показаны пунктирными линиями (зеркала поставленыперпендикулярно к плоскости чертежа). Ясно, что, отразив в зеркале любую половину снежинки, мы получим всё ту же шестилучевую звёздочку

Свойство кристаллов совмещаться с собой в различных положениях путём поворотов, отражений, параллельных переносов либо части или комбинации этих операций. Симметрия внешней формы (огранки) кристалла определяется симметрией его атомного строения, которая обусловливает также и симметрию физических свойств кристалла.

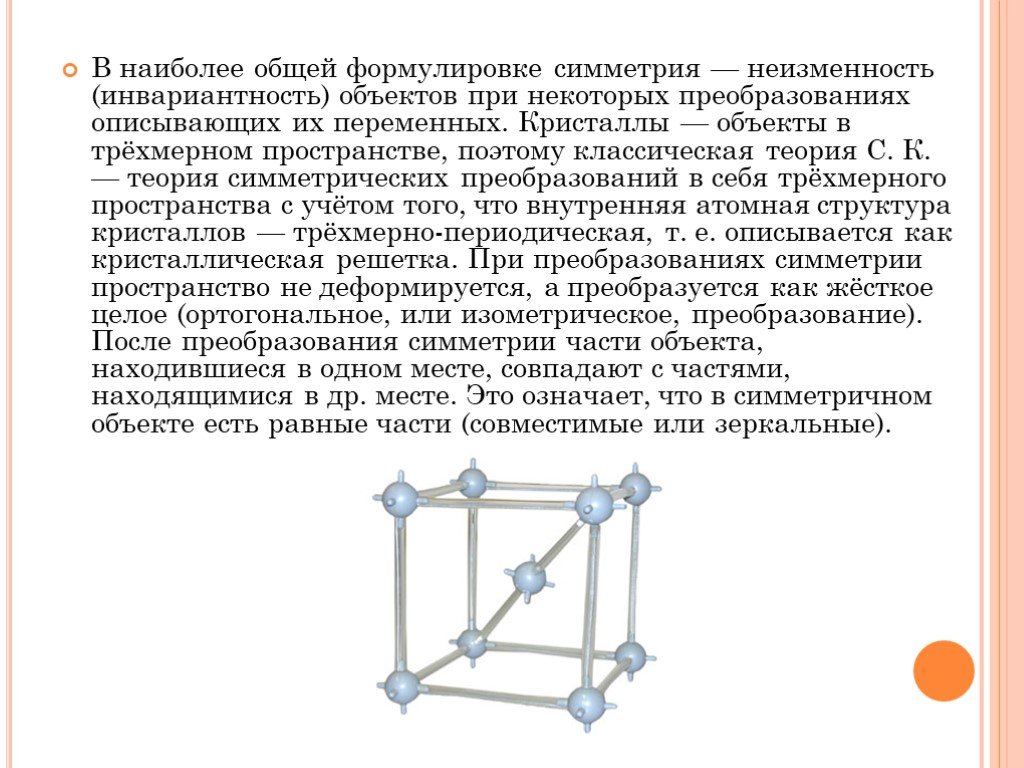
В наиболее общей формулировке симметрия — неизменность (инвариантность) объектов при некоторых преобразованиях описывающих их переменных. Кристаллы — объекты в трёхмерном пространстве, поэтому классическая теория С. К. — теория симметрических преобразований в себя трёхмерного пространства с учётом того, что внутренняя атомная структура кристаллов — трёхмерно-периодическая, т. е. описывается как кристаллическая решетка. При преобразованиях симметрии пространство не деформируется, а преобразуется как жёсткое целое (ортогональное, или изометрическое, преобразование). После преобразования симметрии части объекта, находившиеся в одном месте, совпадают с частями, находящимися в др. месте. Это означает, что в симметричном объекте есть равные части (совместимые или зеркальные).

Точечная симметрия кристаллов

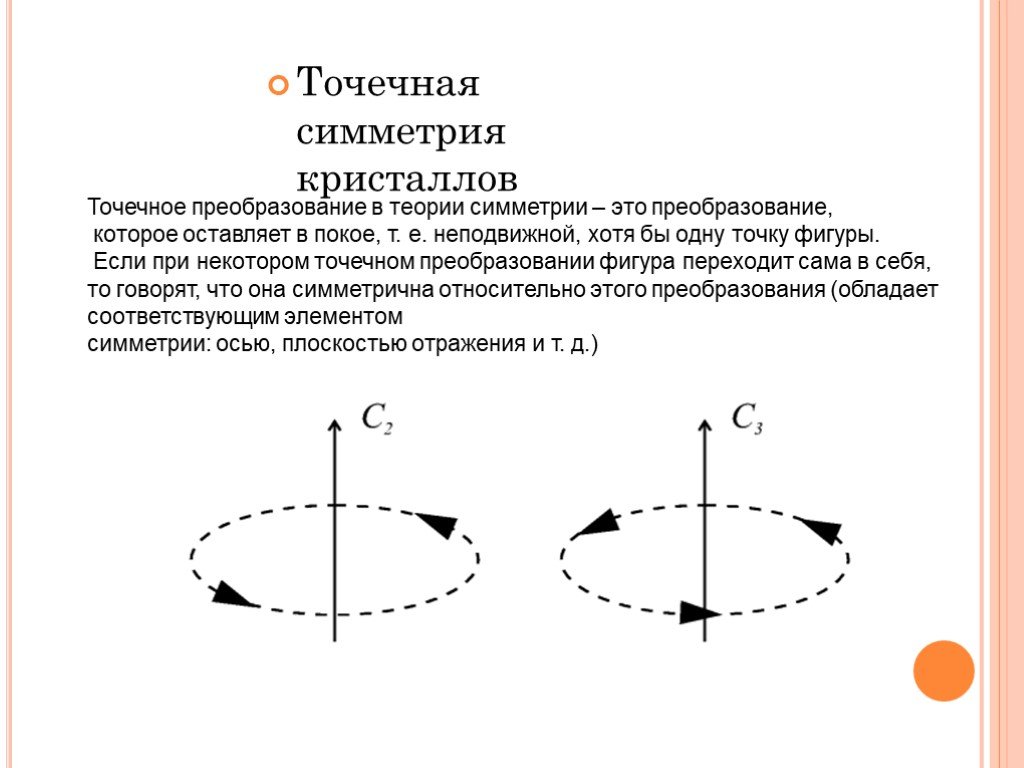
Точечное преобразование в теории симметрии – это преобразование, которое оставляет в покое, т. е. неподвижной, хотя бы одну точку фигуры. Если при некотором точечном преобразовании фигура переходит сама в себя, то говорят, что она симметрична относительно этого преобразования (обладает соответствующим элементом симметрии: осью, плоскостью отражения и т. д.)

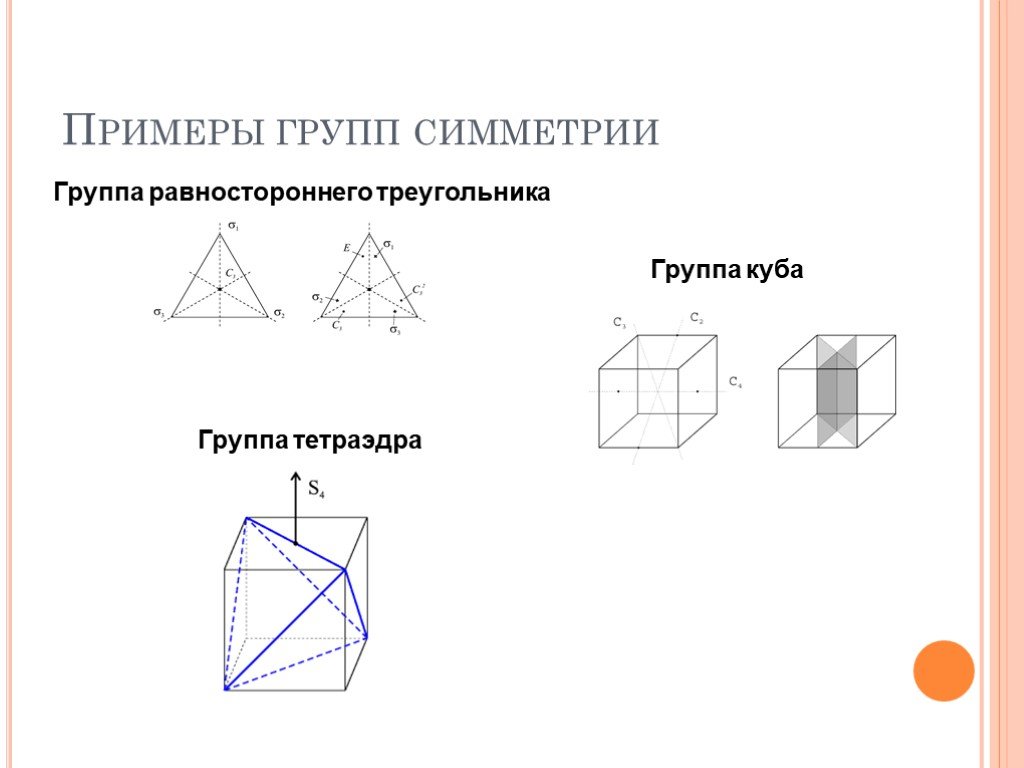
Примеры групп симметрии

Группа равностороннего треугольника

Группа куба Группа тетраэдра

Все это привело человека к мысли, что чтобы сооружение было красивым оно должно быть симметричным. Симметрия использовалась при сооружении культовых и бытовых сооружений в Древнем Египте. Украшения этих сооружений тоже представляют образцы использования симметрии. Но наиболее ярко симметрия проявляется в античных сооружениях Древней Греции, предметах роскоши и орнаментов, украшавших их.

Симметрия в архитектуре

Симметрия в технике

«Природа! Из простейшего вещества творит она противоположнейшие произведения, без малейшего усилия, с величайшим совершенством, и на все кладет какое-то нежное покрывало. У каждого ее создания особенная сущность, у каждого явления отдельное понятие, а все едино» Гёте.

Симметрия в живой природе.

ПОВОРОТНАЯ СИММЕТРИЯ. Говорят, что объект обладает поворотной симметрией, если он совмещается сам с собой. ПЕРЕНОСНАЯ (ТРАНСЛЯЦИОННАЯ) СИММЕТРИЯ. О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние а либо расстояние, кратное этой величине, она совмещается сама с собой. ЗЕРКАЛЬНАЯ СИММЕТРИЯ. Зеркально симметричным считается объект, состоящий из двух половин, которые являются зеркальными двойниками по отношению друг к другу. СИММЕТРИИ ПОДОБИЯ представляют собой своеобразные аналоги предыдущих симметрий с той лишь разницей, что они связаны с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки. КАЛИБРОВОЧНЫЕ СИММЕТРИИ связаны с изменением масштаба.

Виды симметрии.

Симметрией обладают объекты и явления живой природы. Она не только радует глаз и вдохновляет поэтов всех времен и народов, а позволяет живым организмам лучше приспособиться к среде обитания и просто выжить. В живой природе огромное большинство живых организмов обнаруживает различные виды симметрий. Внешняя симметрия может выступить в качестве основания классификации организмов (сферическая, радиальная, осевая и т.д.) Микроорганизмы, живущие в условиях слабого воздействия гравитации, имеют ярко выраженную симметрию формы. В настоящее время хорошо известно, что молекулы органических веществ, составляющие основу живой материи, имеют асимметричный характер, т.е. в состав живого вещества они входят только либо как правые, либо как левые молекулы. Таким образом, каждое вещество может входить в состав живой материи только в том случае, если оно обладает вполне определенным типом симметрии. Например, молекулы всех аминокислот в любом живом организме могут быть только левыми, сахара - только правыми. Это свойство живого вещества и его продуктов жизнедеятельности называют дисимметрией.

СИММЕТРИЯ В ЖИВОЙ ПРИРОДЕ. СИММЕТРИЯ И АСИММЕТРИЯ.

Асимметрия присутствует уже на уровне элементарных частиц и проявляется в абсолютном преобладании в нашей Вселенной частиц над античастицами. Известный физик Ф. Дайсон писал: "Открытия последних десятилетий в области физики элементарных частиц заставляют нас обратить внимание на концепцию нарушения симметрии. Развитие Вселенной с момента ее зарождения выглядит как непрерывная последовательность нарушений симметрии. В момент своего возникновения при грандиозном взрыве Вселенная была симметрична и однородна. По мере остывания в ней нарушается одна симметрия за другой, что создает возможности для существования все большего и большего разнообразия структур. Молекулярная асимметрия открыта Л. Пастером, который первым выделил "правые" и "левые" молекулы винной кислоты: правые молекулы похожи на правый винт, а левые - на левый. Такие молекулы химики называют стереоизомерами. Молекулы-стереоизомеры имеют одинаковый атомный состав, одинаковые размеры, одинаковую структуру - в то же время они различимы, поскольку являются зеркально асимметричными.

Если бы живое существо оказалось в условиях, когда вся пища была бы составлена из молекул противоположной симметрии, не отвечающей дисимметрии этого организма, то оно погибло бы от голода. В неживом веществе правых и левых молекул поровну. Дисимметрия - единственное свойство, благодаря которому мы можем отличить вещество биогенного происхождения от неживого вещества. Таким образом, асимметрию можно рассматривать как разграничительную линию между живой и неживой природой. . Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте. На принципе симметрии основан метод аналогий, предполагающий отыскание общих свойств в различных объектах. На основе аналогий создаются физические модели различных объектов и явлений. Аналогии между процессами позволяют описывать их общими уравнениями.

Специфика строения растений и животных определяется особенностями среды обитания, к которой они приспосабливаются, особенностями их образа жизни. У любого дерева есть основание и вершина, "верх" и "низ", выполняющие разные функции. Значимость различия верхней и нижней частей, а также направление силы тяжести определяют вертикальную ориентацию поворотной оси "древесного конуса" и плоскостей симметрии. Для листьев характерна зеркальная симметрия. Эта же симметрия встречается и у цветов, однако у них зеркальная симметрия чаще выступает в сочетании с поворотной симметрией. Нередки случаи и переносной симметрии (веточки акации, рябины). Интересно, что в цветочном мире наиболее распространена поворотная симметрия 5-го порядка, которая принципиально невозможна в периодических структурах неживой природы. Этот факт академик Н. Белов объясняет тем, что ось 5-го порядка - своеобразный инструмент борьбы за существование, "страховка против окаменения, кристаллизации, первым шагом которой была бы их поимка решеткой" Действительно, живой организм не имеет кристаллического строения в том смысле, что даже отдельные его органы не обладают пространственной решеткой. Однако упорядоченные структуры в ней представлены очень широко. Соты- настоящий конструкторский шедевр. Они состоят из ряда шестигранных ячеек. Это самая плотная упаковка, позволяющая наивыгоднейшим образом разместить в ячейке личинку и при максимально возможном объеме наиболее экономно использовать строительный материал-воск.

СИММЕТРИЯ В МИРЕ РАСТЕНИЙ:

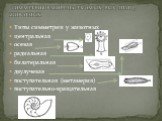
Типы симметрии у животных центральная осевая радиальная билатеральная двулучевая поступательная (метамерия) поступательно-вращательная

СИММЕТРИЯ В МИРЕ НАСЕКОМЫХ, РЫБ, ПТИЦ, ЖИВОТНЫХ

Ось симметрии- это ось вращения. В этом случае у животных, как правило, отсутствует центр симметрии. Тогда вращение может происходить только вокруг оси. При этом ось чаще всего имеет разнокачественные полюса. Например, у кишечнополостных, гидры или актинии, на одном полюсе расположен рот, на другом - подошва, которой эти неподвижные животные прикреплены к субстрату. Ось симметрии может совпадать морфологически с переднезадней осью тела.

Ось симметрии.

Вращательная симметрия. Любой организм обладает вращательной симметрией Для вращательной симметрии существенным характерным элементом являются антимеры. Важно знать, при повороте на какой градус контуры тела совпадут с исходным положением. Максимальный градус поворота 360 , когда при повороте на эту величину контуры тела совпадут.

Типы симметрии. Известны всего два основных типа симметрии – вращательная и поступательная. Кроме того, встречается модификация из совмещения этих двух основных типов симметрии – вращательно-поступательная симметрия.

Если тело вращается вокруг центра симметрии, то через центр симметрии можно провести множество осей и плоскостей симметрии. Если тело вращается вокруг одной гетерополярной оси, то через эту ось можно провести столько плоскостей, сколько антимер имеет данное тело. В зависимости от этого условия говорят о вращательной симметрии определённого порядка. Например, у шестилучевых кораллов будет вращательная симметрия шестого порядка. У гребневиков две плоскости симметрии, и они имеют симметрию второго порядка.

Вращательно-поступательная симметрия. Этот тип симметрии имеет ограниченное распространение в животном мире. Эта симметрия характерна тем, что при повороте на определённый угол часть тела немного проступает вперед и её размеры каждый следующий логарифмически увеличивает на определённую величину. Таким образом, происходит совмещение актов вращения и поступательного движения. Примером могут служить спиральные камерные раковины фораминифер, а также спиральные камерные раковины некоторых головоногих моллюсков ( современный наутилус или ископаемые раковины аммонитов). С некоторым условием к этой группе можно отнести также и некамерные спиральные раковины брюхоногих моллюсков.

Винтовая симметрия есть симметрия относительно комбинации двух преобразований - поворота и переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта. Встречаются левые и правые винты . Примерами природных винтов являются: бивень нарвала (небольшого китообразного, обитающего в северных морях) – левый винт;раковина улитка– правый винт; рога памирского барана – энантиоморфы (один рог закручен по левой, а другой по правой спирали). Спиральная симметрия не бывает идеальной, например, раковина у моллюсков сужается или расширяется на конце.

Винтовая или спиральная симметрия.

С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии. Существует множество видов симметрии как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.

ЗАКЛЮЧЕНИЕ: