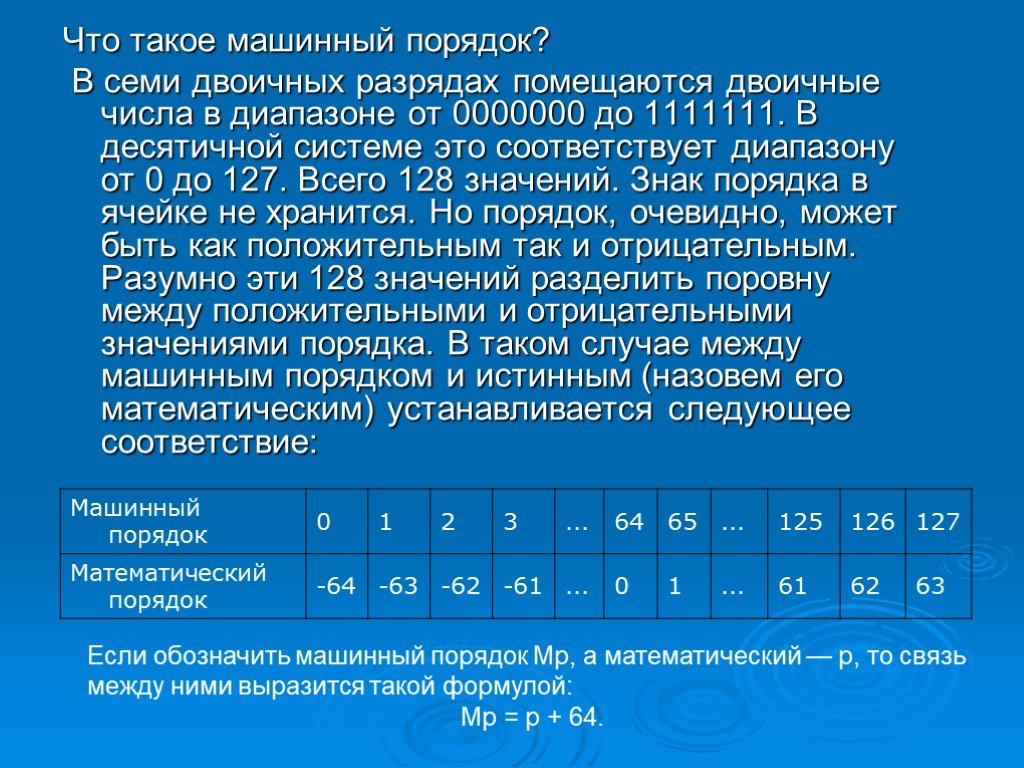
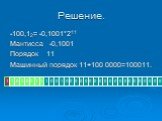
Презентация "Кодирование вещественных чисел" по информатике – проект, доклад

Кодирование вещественных чисел.

Пляшешник А.В. МОУ СОШ №5 города Ржева Тверской области

Для представления вещественных чисел (конечных и бесконечных десятичных дробей) используют формат с плавающей точкой (запятой).

Форма с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления р в некоторой целой степени n, которую называют порядком: R = m * рn m – мантисса, n – порядок, p – основание системы.

Например, число 25,324 можно записать в таком виде: 0.25324х102. Здесь m=0.25324 — мантисса, n=2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна «переплыть», т.е. сместиться десятичная точка в мантиссе. Отсюда название «плавающая точка». Однако справедливы и следующие равенства: 25,324 = 2,5324*101 = 0,0025324*104 = 2532,4*102 и т.п.

Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализованном представлении должна удовлетворять условию: 0,1p ≤ m < 1p.

Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. Значит для рассмотренного числа нормализованным представлением будет: 25,324=0.25324 * 102.

Пусть в памяти компьютера вещественное число представляется в форме с плавающей точкой в двоичной системе счисления (р=2) и занимает ячейку размером 4 байта. В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы. Вот как эта информация располагается в ячейке:

1-й байт 2-й байт 3-й байт 4-й байт

В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы.

Что такое машинный порядок? В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. В десятичной системе это соответствует диапазону от 0 до 127. Всего 128 значений. Знак порядка в ячейке не хранится. Но порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка. В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие:

Если обозначить машинный порядок Мр, а математический — р, то связь между ними выразится такой формулой: Мр = р + 64.

Итак, машинный порядок смещён относительно математического на 64 единицы и имеет только положительные значения. При выполнении вычислений с плавающей точкой процессор это смещение учитывает. В двоичной системе счисления смещение: Мр2 = р2+100 00002

Теперь мы можем записать внутреннее представление числа 25,324 в форме с плавающей точкой. 1)Переведем его в двоичную систему счисления с 24 значащими цифрами. 25,32410= 11001,01010010111100011012 2)Запишем в форме нормализованного двоичного числа с плавающей точкой: 0,110010101001011110001101*10101

Здесь мантисса, основание системы счисления (210=102) и порядок (510=1012)записаны в двоичной системе.

3) Вычислим машинный порядок. Мр2 = 101 + 100 0000 = 100 0101.

4) Запишем представление числа в ячейке памяти.

Знак числа порядок мантисса 31 0

Число в форме с плавающей точкой занимает в памяти компьютера 4 байта (число обычной точности) или 8 байт (число двойной точности). Мы рассмотрели пример представления числа 25,324 обычной точности

Для того, чтобы получить внутреннее представление отрицательного числа -25,324, достаточно в полученном выше коде заменить в разряде знака числа 0 на 1.

Задание.

Представьте двоичное число -100,12 в четырёхбайтовом формате. Представьте число сначала в форме с плавающей запятой.

Решение.

-100,12= -0,1001*211 Мантисса -0,1001 Порядок 11 Машинный порядок 11+100 0000=100011.