Презентация "Представление чисел в памяти компьютера" по информатике – проект, доклад
Презентацию на тему "Представление чисел в памяти компьютера" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 42 слайд(ов).
Слайды презентации
Список похожих презентаций
Представление чисел в памяти компьютера
Электронный калькулятор Перевод чисел Практическая работа № 15 Числа в памяти компьютера. Оглавление. Электронный калькулятор. - специализированное ...Представление чисел в памяти компьютера
Сегодня вы познакомитесь с алгоритмом представления целых чисел в компьютере; Развивающая: способствовать развитию у учащихся интереса к теоретическим ...Системы счисления и двоичное представление информации в памяти компьютера
Пример задания:. Сколько единиц в двоичной записи числа 1025? 1) 1 2) 2 3) 10 4) 11. Решение (вариант 1, прямой перевод): 1) переводим число 1025 ...Представление чисел в различных системах счисления
Система счисления – определенные правила записи чисел и связанные с ними способы выполнения вычислений. Алгоритм записи развернутой формы числа десятичной ...Организация и основные характеристики памяти компьютера
Компьютер – это универсальное (многофункциональное) автоматическое программно управляемое электронное устройство, предназначенное для хранения, обработки ...Представление целых чисел в компьютере
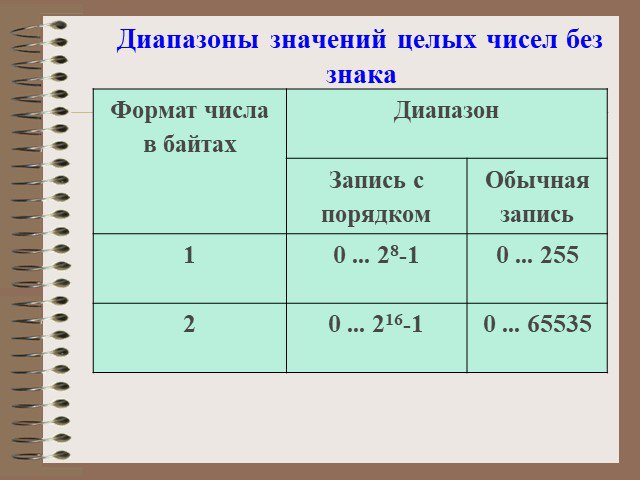
Целые числа без знака. Обычно занимают в памяти компьютера один или два байта и принимают значения: в однобайтовом формате от 000000002 до 111111112 ...Представление чисел в компьютере
Представление чисел в формате с фиксированной запятой. Этот формат используется для хранения целых чисел. Каждому разряду ячейки памяти соответствует ...Представление чисел в компьютере
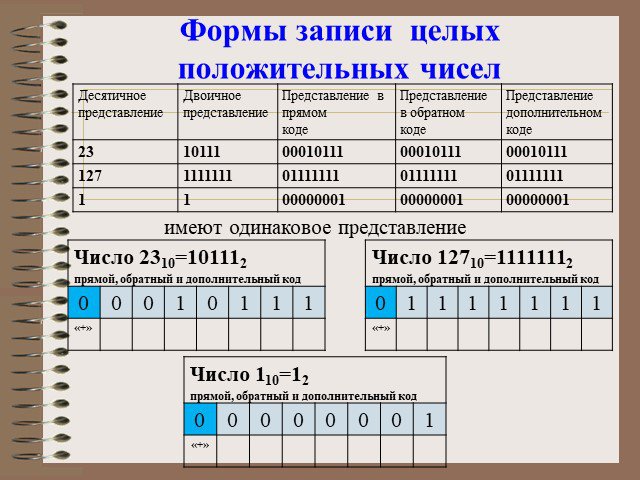
Неотрицательные числа:. 1 число занимает ровно 1 ячейку памяти (8 битов). Самое большое неотрицательное число:. Это число: 1*2^7+1*2^6+1*2^5+1*2^4+1*2^3+1*2^2+1*2^1+1*2^0=255 ...Представление чисел в компьютере
Все числа в ЭВМ должны быть строго определенной длины. Это регулируется понятием РАЗРЯДНАЯ СЕТКА. От разрядной сетки (длины числа) зависит максимальное ...Тексты в памяти компьютера
В чем преимущества компьютера при работе с текстом? 1 - создавать тексты не тратя на это бумаги. 2 - компактное размещение текста на магнитном носителе ...Представление звука в памяти компютера
Физическая природа звука. - Колебания в определенном диапазоне частот , передаваемые звуковой волной через воздух (или другую упругую среду). Процесс ...Информация в памяти компьютера
Информация в памяти компьютера. Языки делятся на естественные (разговорные) и формальные. Представление информации с помощью какого-либо языка часто ...Информация в памяти компьютера. Системы счисления
Как представлена информация в компьютере? Информация в компьютере представлена двумя цифрами 0 и 1. Системы счисления. Позиционные Непозиционные. ...Дискретные модели данных в компьютере. Представление чисел
Образ компьютерной памяти. Главные правила представления данных в компьютере. Правило № 1 Данные (и программы) в памяти компьютера хранятся в двоичном ...Изображения в памяти компьютера
Последовательностями 000011100001111 можно закодировать и графическую информацию. Как это сделать? Два способа представления изображений в цифровом ...Программное обеспечение компьютера
Программа являет собой описание на языке, понятном компьютеру алгоритм действий, необходимых к выполнению с целью решения поставленных задач. Синтез ...Представление информации в форме таблиц
Преобразуйте текстовую информацию в табличную. В понедельник в газетном киоске было продано 6о экземпляров газеты "Спорт", 40 экземпляров газеты "Труд", ...Представление о системе объектов
что такое отношения, связи и взаимодействие объектов; что такое система; каковы основные признаки системы; как построить информационную модель системы. ...Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную
Таблица цифр. Правило Данное двоичное число разбить справа налево на группы по 3 цифры в каждой Если в последней левой группе окажется меньше 3 цифр, ...Представление информации
Форма и язык представления информации. Воспринимая информацию с помощью органов чувств, человек стремиться зафиксировать ее в той или иной форме. ...Конспекты
Представление чисел в памяти компьютера
Методическая разработка урока информатики в 9 классе. . с использованием Сингапурской методики обучения. . . . Учитель: Гатауллина Э.Р. ...Представление текстов в памяти компьютера. Кодировочные таблицы
. Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 247 Красносельского района Санкт-Петербурга. ...Представление чисел в памяти ЭВМ
Конспект урока. . «Представление чисел в памяти ЭВМ». Цель. – научиться производить арифметические действия в основных системах счисления и переводить ...Тексты в памяти компьютера
Учитель информатики МБОУ «Гимназия № 5» г. Брянска. . Прокопович Елена Вячеславна. План-конспект урока. Предмет: Информатика. Класс: 8. ...Назначение и устройство компьютера. Принципы организации внутренней и внешней памяти
Технологическая карта урока. 1. Ф. И. О.учителя: Бобина Алла Владимировна, учитель информатики. ГБОУ школа№494 Выборгского района г.Санкт-Петербурга. ...Представление чисел в компьютере. Арифметические действия над целыми числами. Арифметические операции над числами с плавающей точкой
Тема. Представление чисел в компьютере. Арифметические действия над целыми числами. Арифметические операции над числами с плавающей точкой. Цель ...Кодирование числовой информации. Представление чисел в формате с фиксированной запятой
МОУ СОШ № 18 г.Пензы. . Кодирование числовой информации. Представление чисел в формате с фиксированной запятой (числа со знаком). Цели:. . ...Тексты в памяти компьютера. Редактирование и форматирование текста. Создание надписей
6 класс Урок 6. Тексты в памяти компьютера. Практическая работа №3 (задание 1). Редактирование и форматирование текста. Создание надписей. Краткая ...Кодирование вещественных чисел. Представление чисел в формате с плавающей запятой
МОУ СОШ 3 18 г.Пензы. . Кодирование вещественных чисел. Представление чисел в формате с плавающей запятой. Цели:. научить учащихся представлять ...Тексты в памяти компьютера
Музыка Екатерина Николаевна, МБОУ СОШ №7, г. Сургут. 6 класс. Раздел программы: Компьютер и информация. Тема урока: Тексты в памяти компьютера. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Информатика
Содержит:42 слайд(ов)
Поделись с друзьями:
Скачать презентацию