Конспект урока «Основные этапы разработки и исследования моделей на компьютере» по информатике для 8 класса

Урок 26. Основные этапы разработки и исследования моделей на компьютере.

8 класс

Цели урока: рассмотреть основные этапы разработки и исследования моделей на компьютере; развитие логического мышления, математической речи, интерес к предмету; воспитывать прилежание.

Сопровождение: презентация «Компьютерное моделирование».

Ход урока:

1. Организационный момент.

2. Интеллектуальная разминка.

Задание: Разгадайте ребус и определите тему урока.

3. Постановка темы и цели урока.

Итак, как вы думаете какая тема сегодняшнего урока?

4. Актуализация знаний.

1. Ответьте на вопросы: Что такое алгоритм? Какие виды алгоритмов вы знаете? Что такое блок-схема? Из каких элементов состоит блок-схема? Что такое модель? А моделирование? Из каких этапов состоит процесс решения любой задачи?

2. Поставьте в соответствие.

3. Назовите общий вид условного оператора.

5. Изучение нового материала.

Класс делится на две группы.

Задание: Составьте алгоритм решения задач с помощью компьютера. (Задание выполняется на листах А4)

Проводится проверка предложенных алгоритмов с эталоном.

Итак, решение задач с помощью компьютера включает в себя следующие основные этапы, часть из которых осуществляется без участия компьютера (рис.1).

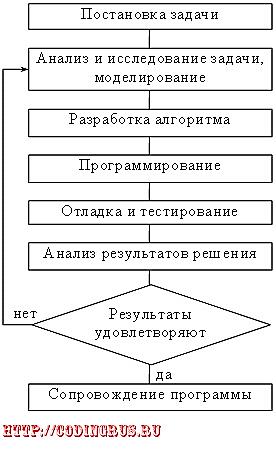
Рис.1. Этапы решения задач с использованием компьютера

Как видно из рисунка, процесс решения любой задачи начинается с постановки задачи. От того насколько точно будет поставлена задача, будет зависеть и результат ее решения. На данном этапе выполняются следующие действия:

- формулировка условия задачи;

- определение конечных целей решения задачи;

- определение формы выдачи результатов;

- описание данных (их типов, диапазонов величин, структуры и т.п.).

На уроках алгебры вы сейчас учитесь решать квадратные уравнения.

- Как вы думаете, можно ли их решать на компьютере?

- Да.

Рассмотрим процесс решения задачи с помощью компьютера на примере решения квадратного уравнения.

- Как вы думаете, какой из видов алгоритмов здесь подойдет?

- Алгоритм с ветвлением.

Проблемный вопрос (вопрос для исследования):

Сколько надо использовать условий в алгоритме решения квадратного уравнения?

Гипотеза исследования:

В алгоритме решения квадратного уравнения надо использовать _________ условий(я).

(Квадратное уравнение имеет либо два, либо одно или вообще не имеет действительного решения.)

Цель исследования:

Составить алгоритм решения квадратных уравнений для последующего программирования.

План исследования – этапы решения задач с помощью компьютера.

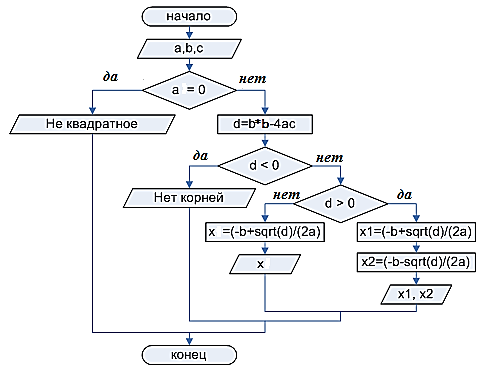
Напишите программу на языке Pascal по этому алгоритму.

program Quadratic;

var a,b,c,d: real;

begin

write('a = '); readln(a);

write('b = '); readln(b);

write('c = '); readln(c);

if (a=0) then writeln('Не квадратное уравнение.');

else d := b*b-4*a*c;

if (dнет корней');

else if (d>0) then

begin

writeln('x1 = ',(-b + Sqrt(d))/(2*a):3:3);

writeln('x2 = ',(-b - Sqrt(d))/(2*a):3:3);

end

else writeln('x = ',(-b+Sqrt(d))/(2*a):3:3);

end.

Анализ результатов решения уравнения вида ax² + bx + c = 0:

6. Домашнее задание:

1. Повторить основные этапы решения задач на компьютере.

2. Составить алгоритм решения не полных квадратных уравнений.

Проблемный вопрос

(вопрос для исследования):

Сколько надо использовать условий в алгоритме решения квадратного уравнения?

Гипотеза исследования:

В алгоритме решения квадратного уравнения надо использовать _________ условий(я).

Цель исследования:

Составить алгоритм решения квадратных уравнений для последующего программирования.

Рассмотрим процесс решения задачи с помощью компьютера на примере решения квадратного уравнения.

На шаге определения конечных результатов следует четко сформулировать требования к результатам решения. В нашем примере, эти требования можно описать следующим образом:

Следующим этапов процесса решения является анализ и исследование задачи, построение модели. На данном этапе следует, прежде всего, проанализировать существующие аналоги. В некоторых случаях можно избежать этапа построения алгоритма и создания программы, благодаря использованию одной из многих ранее созданных программ. Такие библиотеки алгоритмов (программ) существуют практически по всем областям науки и техники.

Предположим, что для нашей задачи аналогов не нашлось. Тогда следует проанализировать собственные технические и программные средства. Когда техническая и информационная база достаточны для решения задачи, приступают к разработке математической модели, которая основана на некоторых упрощениях, и это делает этап построения математической модели весьма ответственным, ведь неправильно выбранная модель приведет к неверным результатам.

Конечно, результаты вычислительного эксперимента могут оказаться и не соответствующими действительности, если в модели не будут учтены какие-то важные стороны действительности.

Итак, создавая математическую модель для решения задачи, нужно:

1. выделить предположения, на которых будет основываться математическая модель;

2. определить, что считать исходными данными и результатами;

3. записать математические соотношения, связывающие результаты с исходными данными.

При построении математических моделей далеко не всегда удается найти формулы, явно выражающие искомые величины через данные. В таких случаях используются математические методы, позволяющие дать ответы той или иной степени точности.

Существует не только математическое моделирование какого-либо явления, но и визуально-натурное моделирование, которое обеспечивается за счет отображения этих явлений средствами машинной графики, т.е. перед исследователем демонстрируется своеобразный "компьютерный мультфильм", снимаемый в реальном масштабе времени. Наглядность здесь очень высока.

Когда математическая модель получается достаточно сложной, может потребоваться разработать структуру данных.

В нашем примере существующая физическая система описывается с помощью упрощенной математической модели.

Математическая модель описывает объект моделирования с помощью уравнений.

Следующим этапом процесса решения задачи с помощью компьютера является разработка алгоритма. На этом этапе выполняются выбор метода проектирования алгоритма, выбор формы записи алгоритма (блок-схемы, псевдокод и др.), выбор тестов и метода тестирования и, наконец, проектирование алгоритма.

Необходимо помнить, что на данном этапе еще неизвестно, на каком языке программирования будет реализовываться алгоритм, поэтому следует описывать его на универсальном языке (например, математическом), который впоследствии можно перевести на любой язык программирования.

Построим алгоритм, который позволяет определять значения результатов при различных значениях аргументов. Построенный алгоритм записываем в виде блок-схемы (рис. 2.1).

После того, как алгоритм описан, можно приступать к этапу программирования, на котором выполняется следующее:

- выбор языка программирования;

- уточнение способов организации данных;

- запись алгоритма на выбранном языке программирования.

Вот как будет выглядеть наш алгоритм на языке программирования Паскаль.

В общем случае, процесс разработки программы можно выразить следующей формулой:

Поэтому недостаточно написать текст программы. Необходимо полученный вариант программы протестировать, т.к. наличие ошибок в только что разработанной программе – это вполне нормальное закономерное явление. Практически невозможно составить реальную (достаточно сложную) программу без ошибок. Нельзя делать вывод, что программа правильна, лишь на том основании, что она не отвергнута машиной и выдала результаты. Все, что достигнуто в этом случае, это получение каких-то результатов, не обязательно правильных. В программе при этом может оставаться большое количество логических ошибок. Ответственные участки программы проверяются с использованием методов доказательства правильности программ.

Как проконтролировать текст программы до выхода на компьютер?

Текст программы можно проконтролировать за столом с помощью просмотра, про-верки и прокрутки.

• Просмотр. Текст программы просматривается на предмет обнаружения описок и расхождений с алгоритмом. Нужно просмотреть организацию всех циклов, что-бы убедиться в правильности операторов, задающих кратности циклов. Полезно посмотреть еще раз условия в условных операторах, аргументы в обращениях к подпрограммам и т.п.

• Проверка. При проверке программы программист по тексту программы мысленно старается восстановить тот вычислительный процесс, который определяет про-грамма, после чего сверяет его с требуемым процессом. На время проверки нужно "забыть", что должна делать программа , и "узнавать" об этом по ходу её проверки. Только после окончания проверки программы можно "вспомнить" о том, что она должна делать и сравнить реальные действия программы с требуемыми.

• Прокрутка. Основой прокрутки является имитация программистом за столом выполнения программы на машине. Для выполнения прокрутки приходится задаваться какими-то исходными данными и производить над ними необходимые вычисления. Прокрутка — трудоемкий процесс, поэтому ее следует применять лишь для контроля логически сложных участков программ. Исходные данные должны выбираться такими, чтобы в прокрутку вовлекалось большинство ветвей программы.

Отладка и тестирование

Отладка программы – это процесс поиска и устранения ошибок в программе, произ-водимый по результатам её прогона на компьютере.

Тестирование (англ. test — испытание) — это испытание, проверка правильности работы программы в целом, либо её составных частей.

Отладка программы:

• при отладке происходит локализация и устранение синтаксических ошибок и явных ошибок кодирования;

• в процессе же тестирования проверяется работоспособность программы, не содержащей явных ошибок.

Английский термин debugging ("отладка") буквально означает "вылавливание жучков". Термин появился в 1945 г., когда один из первых компьютеров — "Марк-1" прекратил работу из-за того, что в его электрические цепи попал мотылек и заблокировал своими останками одно из тысяч реле машины.

В чем заключается отладка?

В современных программных системах (Turbo Basic, Turbo Рascal, Turbo C и др.) от-ладка осуществляется часто с использованием специальных программных средств, назы-ваемых отладчиками. Эти средства позволяют исследовать внутреннее поведение программы.

Программа-отладчик обычно обеспечивает следующие возможности:

• пошаговое исполнение программы с остановкой после каждой команды (оператора);

• просмотр текущего значения любой переменной или нахождение значения любого выражения, в том числе, с использованием стандартных функций; при необходимости можно установить новое значение переменной;

• установку в программе "контрольных точек", т.е. точек, в которых программа временно прекращает свое выполнение, так что можно оценить промежуточные результаты, и др.

Что такое тест и тестирование?

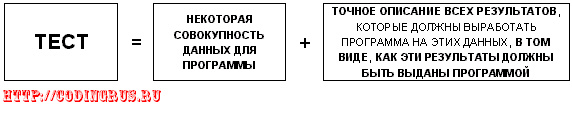
Как бы ни была тщательно отлажена программа, решающим этапом, устанавливающим ее пригодность для работы, является контроль программы по результатам ее выпол-нения на системе тестов.

Программу условно можно считать правильной, если её запуск для выбранной системы тестовых исходных данных во всех случаях дает правильные результаты.

Но, как справедливо указывал известный теоретик программирования Э. Дейкстра, тестирование может показать лишь наличие ошибок, но не их отсутствие. Нередки случаи, когда новые входные данные вызывают "отказ" или получение неверных результатов работы программы, которая считалась полностью отлаженной.

Для реализации метода тестов должны быть изготовлены или заранее известны эталонные результаты.

Вычислять эталонные результаты нужно обязательно до, а не после получения машинных результатов.

В противном случае имеется опасность невольной подгонки вычисляемых значений под желаемые, полученные ранее на машине.

Какими должны быть тестовые данные?

Тестовые данные должны обеспечить проверку всех возможных условий возникновения ошибок:

• должна быть испытана каждая ветвь алгоритма;

• очередной тестовый прогон должен контролировать нечто такое, что еще не было проверено на предыдущих прогонах;

• первый тест должен быть максимально прост, чтобы проверить, работает ли программа вообще;

• арифметические операции в тестах должны предельно упрощаться для уменьшения объема вычислений;

• количества элементов последовательностей, точность для итерационных вычислений, количество проходов цикла в тестовых примерах должны задаваться из соображений сокращения объема вычислений;

• минимизация вычислений не должна снижать надежности контроля;

• тестирование должно быть целенаправленным и систематизированным, так как случайный выбор исходных данных привел бы к трудностям в определении ручным способом ожидаемых результатов; кроме того, при случайном выборе тестовых данных могут оказаться непроверенными многие ситуации;

• усложнение тестовых данных должно происходить постепенно.

Пример. Система тестов для задачи нахождения корней квадратного уравнения

ax2 + bx + c = 0:

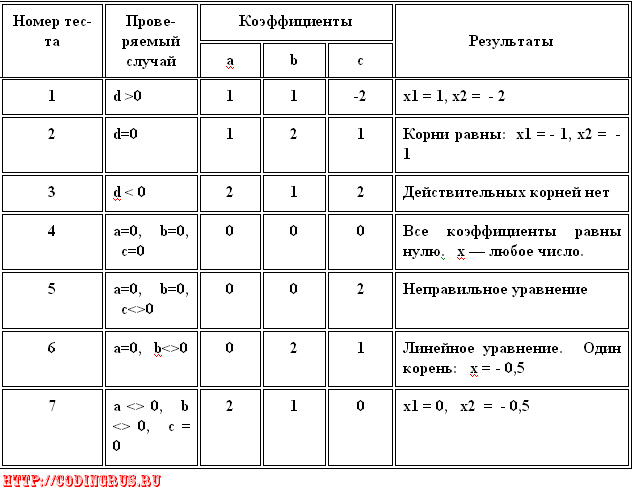
Этапы процесса тестирования

Процесс тестирования можно разделить на три шага.

1. Проверка в нормальных условиях. Предполагает тестирование на основе данных, которые характерны для реальных условий функционирования программы.

2. Проверка в экстремальных условиях. Тестовые данные включают граничные значения области изменения входных переменных, которые должны восприниматься программой как правильные данные. Типичными примерами таких значений являются очень маленькие или очень большие числа и отсутствие данных. Еще один тип экстремальных условий — это граничные объемы данных, когда массивы состоят из слишком малого или слишком большого числа элементов.

3. Проверка в исключительных ситуациях. Проводится с использованием данных, значения которых лежат за пределами допустимой области изменений. Известно, что все программы разрабатываются в расчете на обработку какого-то ограниченного набора данных. Поэтому важно получить ответ на следующие вопросы:

- что произойдет, если программе, не рассчитанной на обработку отрицательных и ну-левых значений переменных, в результате какой-либо ошибки придется иметь дело как раз с такими данными?

- как будет вести себя программа, работающая с массивами, если количество их элементов превысит величину, указанную в объявлении массива?

- что произойдет, если числа будут слишком малыми или слишком большими?

Наихудшая ситуация складывается тогда, когда программа воспринимает неверные данные как правильные и выдает неверный, но правдоподобный результат.

Программа должна сама отвергать любые данные, которые она не в состоянии обрабатывать правильно.

Характерные ошибки при компьютерном решении задач

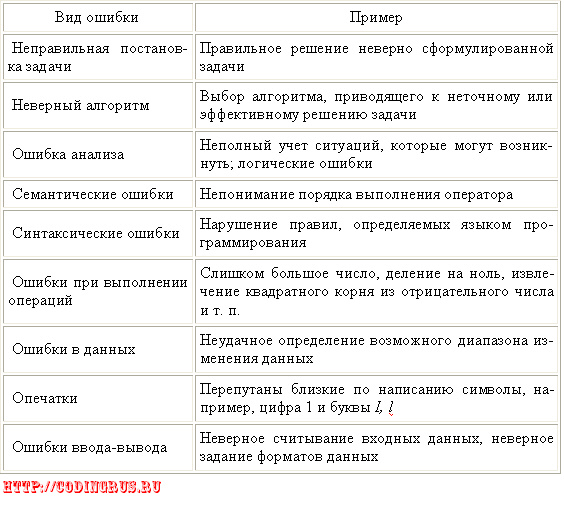
Ошибки могут быть допущены на всех этапах решения задачи — от ее постановки до оформления. Разновидности ошибок и соответствующие примеры приведены в таблице:

Разновидности ошибок

Является ли отсутствие синтаксических ошибок свидетельством правильности программы?

Обычно синтаксические ошибки выявляются на этапе трансляции. Многие же другие ошибки транслятору выявить невозможно, так как транслятору неизвестны замыслы программиста.

Отсутствие сообщений машины о синтаксических ошибках является необходимым,

но не достаточным условием, чтобы считать программу правильной.

Примеры синтаксических ошибок:

- пропуск знака пунктуации;

- несогласованность скобок;

- неправильное формирование оператора;

- неверное образование имен переменных;

- неверное написание служебных слов;

- отсутствие условий окончания цикла;

- отсутствие описания массива и т.п.

Какие ошибки не обнаруживаются транслятором?

Существует множество ошибок, которые транслятор выявить не в состоянии, если используемые в программе операторы сформированы верно. Приведем примеры таких ошибок.

Логические ошибки:

- неверное указание ветви алгоритма после проверки некоторого условия;

- неполный учет возможных условий;

- пропуск в программе одного или более блоков алгоритма.

Ошибки в циклах:

- неправильное указание начала цикла;

- неправильное указание условий окончания цикла;

- неправильное указание числа повторений цикла;

- бесконечный цикл.

Ошибки ввода-вывода; ошибки при работе с данными:

- неправильное задание тип данных;

- организация считывания меньшего или большего объёма даных, чем требуется;

- неправильное редактирование данных.

Ошибки в использовании переменных:

- использование переменных без указания их начальных значений;

- ошибочное указание одной переменной вместо другой.

Ошибки при работе с массивами:

- массивы предварительно не обнулены;

- массивы неправильно описаны;

- индексы следуют в неправильном порядке.

Ошибки в арифметических операциях:

- неверное указание типа переменной (например, целочисленного вместо вещественного);

- неверное определение порядка действий;

- деление на нуль;

- извлечение квадратного корня из отрицательного числа;

- потеря значащих разрядов числа.

Все эти ошибки обнаруживаются с помощью тестирования.

Сопровождение программ – завершающий этап решения задач с использованием компьютера. Сопровождение программ — это работы, связанные с обслуживанием программ в процессе их эксплуатации

Многократное использование разработанной программы для решения различных задач заданного класса требует проведения следующих дополнительных работ:

- исправление обнаруженных ошибок;

- модификация программы для удовлетворения изменяющихся эксплуатационных требований;

- доработка программы для решения конкретных задач;

- проведение дополнительных тестовых просчетов;

- внесение исправлений в рабочую документацию;

- усовершенствование программы и т.д.

Применительно ко многим программам работы по сопровождению поглощают более половины затрат, приходящихся на весь период времени существования программы (начиная от выработки первоначальной концепции и кончая моральным ее устареванием) в стоимостном выражении.

Программа, предназначенная для длительной эксплуатации, должна иметь соответствующую документацию и инструкцию по её использованию.