Конспект урока «Решение задач на проценты» по алгебре

Тема: Решение задач на проценты.

Цели: формирование навыков решения задач на проценты.

Ход урока.

1. Орг момент.

2. Работа на уроке.

Рассмотрим три основных типа задач на проценты.

Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача из учебника "Виленкин 5 класс"

№ 1569

Предприятие изготовило за квартал 500 насосов, из которых 60 % имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?

Решение:

Найдем 60 % от 500 (общее количество насосов).

60 % = 0,6

500 • 0,6 = 300 насосов высшей категории качества.

Ответ: 300 насосов высшей категории качества.

Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать текст. Если вам встречаются слова «который», «что составляет» и «который составляет», скорее всего перед вами задача «число по его проценту».

Задача из учебника «Виленкин 5 класс»

№ 1536

Ученик прочитал 138 страниц, что составляет 23 % числа всех страниц в книге. Сколько страниц в книге?

Решение:

Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую прочитал ученик (138 страниц) составляет 23 % от общего количества страниц в книге. Так как 138 стр. - это всего лишь часть, само количество страниц, естественно, будет больше 138. Это поможет нам при проверке.

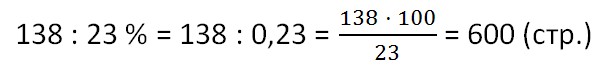
Проверка: 600 > 138 (это означает, что 138 является частью 600).

Ответ: 600 (стр.) - общее количество страниц в книге.

Сколько процентов одно число составляет от другого

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100 %.

Задача из учебника «Виленкин 5 класс»

№ 1609

Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелый арбузы?

Решение:

О чем спрашивают? О незрелых арбузах. Значит, 16 делим на общее количество арбузов и умножаем на 100 %.

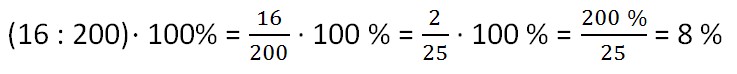
Ответ: 8 % - составляют незрелые арбузы от всех арбузов.

Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что называется концентрацией раствора.

Концентрация раствора - это часть, которую составляет масса растворённого вещества от массы всего раствора.

• 9%-я концентрация раствора соли - это 9 грамм соли в 100 граммах раствора.

Задача из Петерсона 6 класс (2010 г.)

№ 322 (2)

Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)

Используя определение концентрации данное выше, решим задачу следующим образом.

• 1 кг - масса растворённого вещества (соли)

• 9 кг - масса воды в растворе (не путать с общей массой раствора)

• 9 + 1 = 10 кг - общая масса раствора.

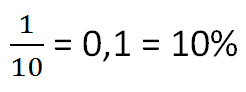
Ответ: 10% - концентрация раствора.

Задача из Петерсона 6 класс (2010 г.)

Теперь решим обратную задачу.

№ 353(2)

Сколько соли получится при выпаривании 375 граммов 12%-го раствора?

Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации. Не забудем предварительно перевести процент в десятичную дробь.

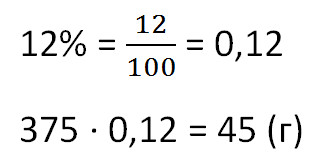
Ответ: 45 г соли.

Сложная задача на растворы

В растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70. Сколько грамм соли было первоначально в растворе?

Для составления пропорции обозначим за x первоначальную массу соли в растворе, а за y массу воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет

100% - 40%= 60%

Изобразим графически условия задачи.

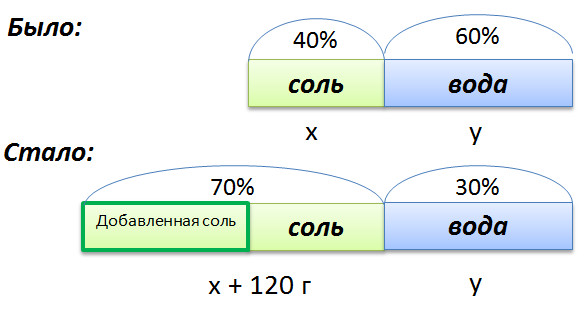
Составим пропорцию, связывающую эти величины до добавления соли.

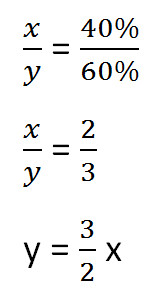
Для решения задачи нам надо определить какая из неизвестных (x или y) остаётся неизменной после добавления соли.

Этой величиной является масса воды в растворе (y).

Выразим её, учитывая изменения в растворе после добавления соли.

• (x + 120) г - масса соли в новом растворе

• 100% - 70% = 30% - процентное содержание воды в новом растворе.

Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших после добавления соли.

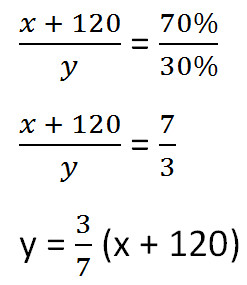
Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и после добавления соли и решим уравнение.

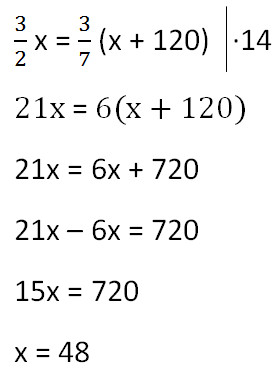
Ответ: 48 г - масса соли в первоначальном растворе.

Прежде чем перейти к задачам на вклады и скидки, необходимо разобраться зачем вообще люди кладут деньги в банк и как найти выгодную скидку.

Задачи по вкладам

Естественно, люди кладут деньги в банк (открывают вклад), не по доброте душевной. Вклады открываются с целью получения прибыли. Банк предлагает следующее: вы кладёте в банк определённую сумму на определённый срок. Например, на год. В течение года вы не сможете воспользоваться своими деньгами (ими будет пользоваться банк), но за это банк вам заплатит, вернув через год не только вложенную вами сумму, но и небольшое вознаграждение.

Какова будет сумма вознаграждения? Для её нахождения банк устанавливает процент годовых. Если вы умножите сумму вашего вклада на процент годовых, вы найдёте, какое вознаграждение добавит банк к вашему вкладу.

Рассмотрим задачи на эти темы из учебников Петерсона и Виленкина.

Задача из Петерсона

Разберем из учебника задачу Петерсон .

Вкладчик внес в банк 1200 р. В какую сумму вклад превратится через год, если банк начисляет доход в размере 4 % годовых?

Решение:

Найдем какое вознаграждение банк доложит вкладчику. Для этого умножим 1200 р. на процент годовых 4%.

4% = 0,04

1200 • 0, 04 = 48 р. - такое вознаграждение доложит банк вкладчику через год.

Теперь найдем общую сумму, которую заберет вкладчик через год.

1200 + 48 = 1248 р. - в такую сумму превратится вклад через год.

Ответ: 1248 р. - в такую сумму превратится вклад через год.

Задачи на скидку (уценку)

Скидка - это понижение цены товара или услуги. Чаще всего скидку указывают в процентах. Поэтому, чтобы найти на сколько в рублях понизилась цена товара, нужно цену товара умножить на процент скидки.

Задача из ГИА 9 класс

Цена изделия составляет 5000 р. На изделие предложена скидка 10%. Найти цену товара с учетом скидки.

Решение:

Найдем скидку в рублях.

10% = 0,1

5000 • 0,1 = 500 р. - скидка в рублях.

Теперь найдем цену товара с учетом скидки.

5000 - 500 = 4500 р. - цена товара с учетом скидки.

Ответ: 4500 р. - цена товара с учетом скидки.