Презентация "Описательная статистика" по математике – проект, доклад

© Бахова А.Б.учитель математики МОУ СОШ №6, г.Нарткала, КБР

Презентация № 5 по теме: «Описательная статистика» - 7 класс

Наибольшее и наименьшее значение.

Пример 1

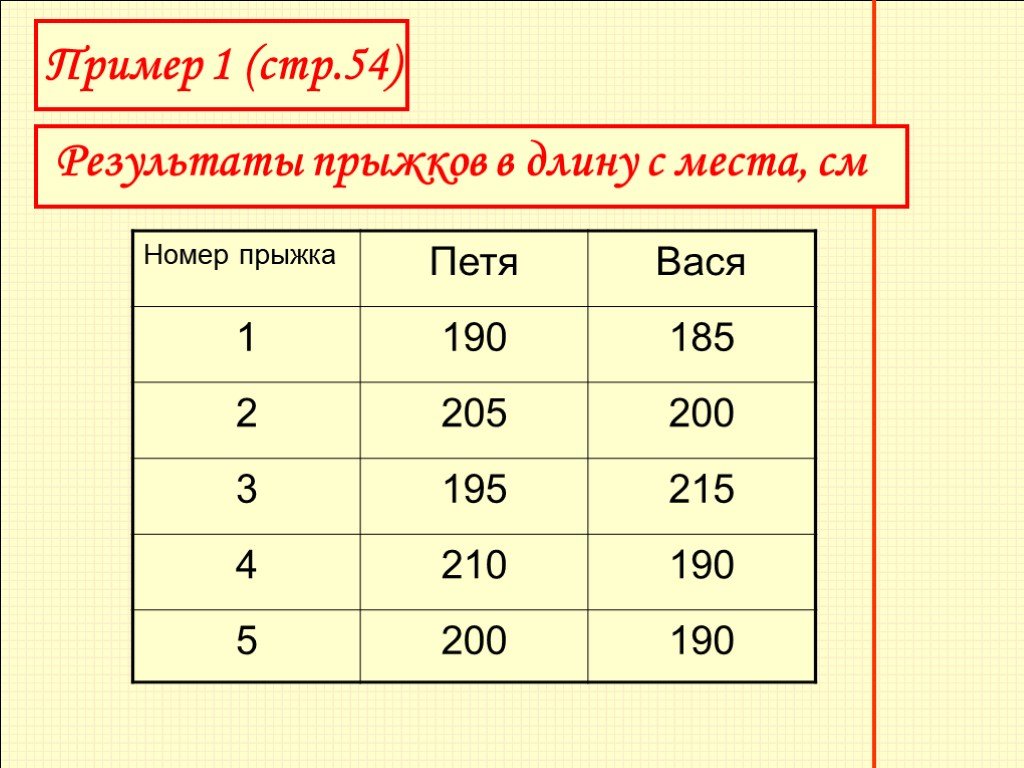
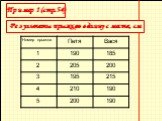
Петя и Вася поспорили, кто лучше прыгает в длину с места. Чтобы избежать случайности, они решили, что будут прыгать по очереди 5 раз. Результаты своих прыжков в сантиметрах они записали в таблицу.

Результаты прыжков в длину с места, см

Пример 1 (стр.54)

Определение

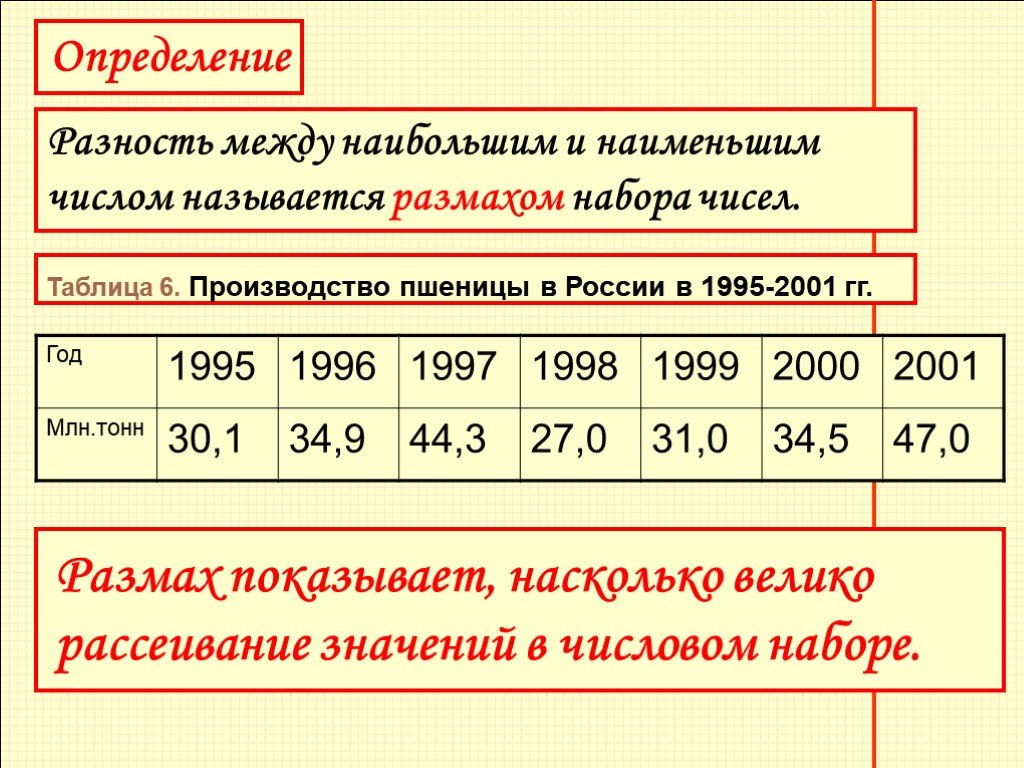
Разность между наибольшим и наименьшим числом называется размахом набора чисел.

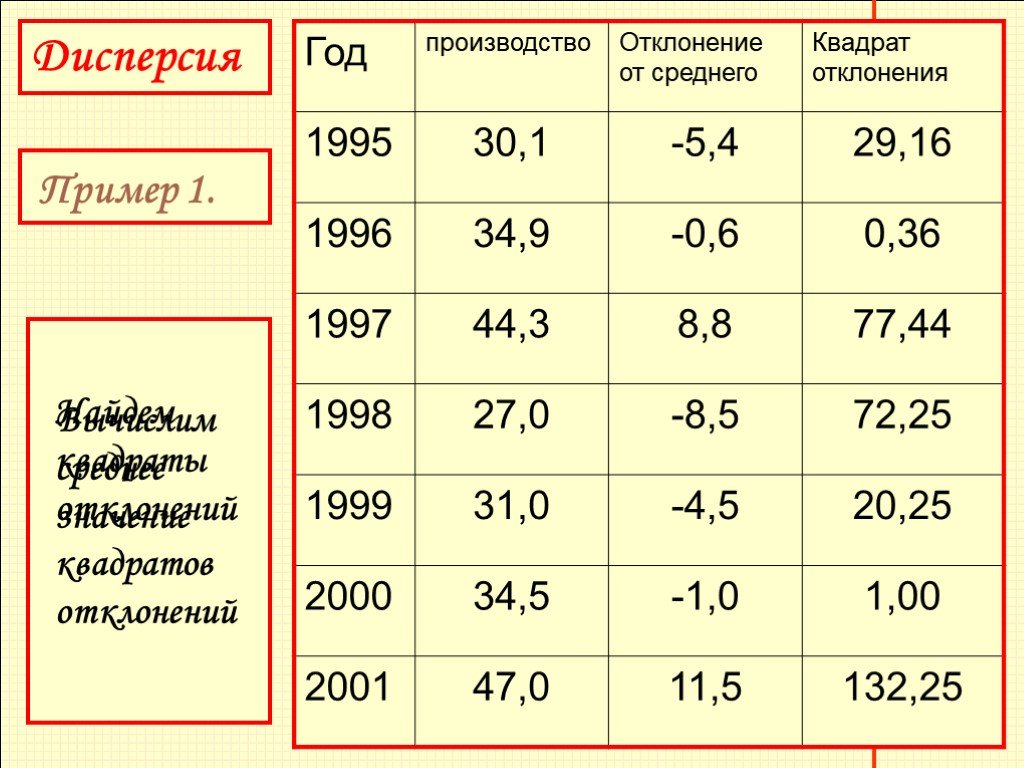
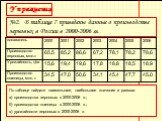
Таблица 6. Производство пшеницы в России в 1995-2001 гг.

Размах показывает, насколько велико рассеивание значений в числовом наборе.

При изучении учебной нагрузки учащихся выделили группу из 12 семиклассников. Их попросили отметить в определенный день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные: 23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.

27 – среднее значение

Наибольшее значение – 37; наименьшее значение – 18;

Размах ряда равен 37 – 18 = 19

При анализе сведений о времени, затраченном семиклассниками на выполнение домашнего задания по алгебре, нас могут интересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели. Интересно, например, знать, какой расход времени является типичным для выделенной группы учащихся, то есть какое число встречается в ряду данных чаще всего. Нетрудно заметить, что таким числом является число 25. Говорят, что число 25 – мода рассматриваемого ряда.

Модой ряда чисел называется число, чаще других встречающееся в данном ряду.

Ряд чисел может иметь более одной моды или не иметь моды совсем.

Рассмотрим еще пример. Пусть, проведя учет деталей, изготовленных за смену рабочими одной бригады, получили такой ряд данных: 36, 35, 35, 36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38, 36, 39, 36.

Найдем для него среднее арифметическое, размах и моду. Для этого удобно предварительно составить из полученных данных упорядоченный ряд чисел, т. е. такой ряд, в котором каждое последующее число не меньше (или не больше) предыдущего. Получим: 35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 38, 38, 38, 39, 39, 39, 39. Вычислим среднее арифметическое:

Размах ряда равен . Мода данного ряда равна 36, так как число 36 чаще всего встречается в этом ряду.

Например, в ряду чисел 47, 46, 50, 52, 47, 52, 49, 45, 43, 53 две моды – это числа 47 и 52, а в ряду чисел 69, 68, 66, 80, 67, 65, 71, 74, 63, 73, 72 моды нет.

Моду ряда данных обычно находят тогда, когда хотят выявить некоторый типичный показатель. Например, если изучаются данные о размерах мужских сорочек, проданных в определенный день в универмаге, то удобно воспользоваться таким показателем, как мода, который характеризует размер, пользующийся наибольшим спросом. Находить в этом случае среднее арифметическое не имеет смысла. Мода является наиболее приемлемым показателем при выявлении, например, расфасовки некоторого товара, которой отдают предпочтение покупатели; цены на товар данного вида, наиболее распространенной на рынке, и т. п.

Итак, средняя выработка рабочих за смену составляет примерно 37 деталей; различие в выработке рабочих не превосходит 4 деталей; типичной является выработка, равная 36 деталям.

Упражнения

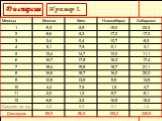
№1. Найдите наибольшее и наименьшее значение, размах, среднее значение, медиану и моду набора чисел: а) 12, 7, 25, 3, 19, 15; б) 17, 19, 5, 41, 47, 13, 19.

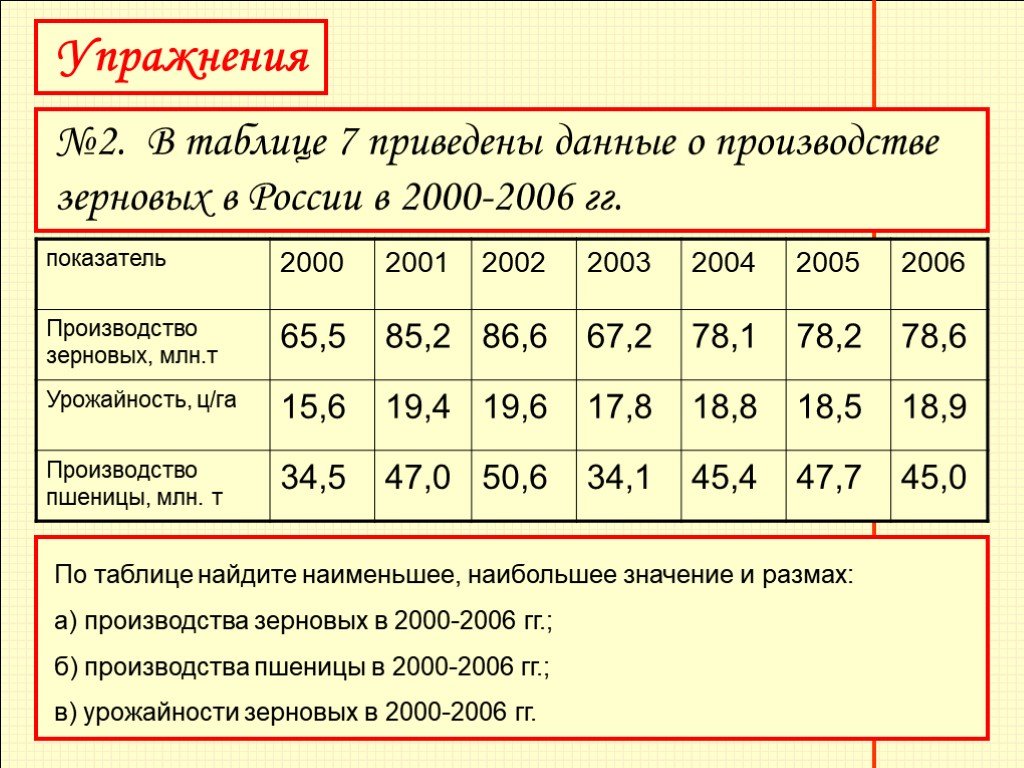
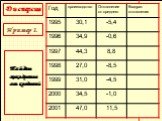
№2. В таблице 7 приведены данные о производстве зерновых в России в 2000-2006 гг.

По таблице найдите наименьшее, наибольшее значение и размах: а) производства зерновых в 2000-2006 гг.; б) производства пшеницы в 2000-2006 гг.; в) урожайности зерновых в 2000-2006 гг.

Отклонения

Попробуем узнать, как числа некоторого набора расположены по отношению к своему среднему значению. Зная только размах, разность между наибольшим и наименьшим значением, мы не можем судить о том, как расположены числа в имеющемся наборе. Для примера возьмем набор 1, 6, 7, 9, 12. Вычислим среднее арифметическое: (1+6+7+9+12):5=7. Найдем отклонение каждого числа от среднего: 1-7=-6, 6-7=-1, 7-7=0, 9-7=2, 12-7=5.

Отклонения (продолжение)

Получился новый набор -6, -1, 0, 2, 5 , который состоит из отклонений. Если число меньше среднего, то его отклонение отрицательно, если число больше среднего, то его отклонение положительно. В одном случае – для числа 7, которое совпало со средним арифметическим, - отклонение равно нулю. По набору отклонений можно судить о том, насколько разнообразны числа в наборе. Если отклонения малы, то числа в наборе расположены близко к среднему арифметическому. А если среди отклонений есть большие по модулю, то числа в наборе сильно разбросаны.

Для любого набора, если только не все числа в нем равны, часть отклонений будет положительна, а часть – отрицательна. При этом сумма всех отклонений равна 0. Убедимся в этом на нашем примере: -6+(-1)+0+2+5=0. В этом состоит основное свойство отклонений: сумма отклонений чисел от среднего арифметического этих чисел равна нулю.

Дисперсия

Наиболее полной характеристикой разброса набора чисел является набор их отклонений от среднего арифметического. Но когда набор чисел велик, рассматривать набор отклонений практически неудобно. Нужно описать разнообразие чисел в наборе одной характеристикой, одним числом. Размах – слишком грубая мера разброса чисел в наборе, поскольку учитывает только два из них – наименьшее и наибольшее. Можно попробовать взять «среднее отклонение». Но сумма отклонений всегда равна нулю, поэтому среднее арифметическое отклонений тоже равно нулю и его нельзя использовать как меру разброса.

Чтобы судить о разбросе, принято складывать не сами отклонения, а их квадраты. Квадраты отклонений неотрицательны, поэтому сумма квадратов отклонений зависит только от абсолютных величин отклонений, а не от их знаков. Чем больше отклонения чисел от среднего арифметического, тем больше будет сумма квадратов отклонений. Для того чтобы мера разброса чисел не зависела от их количества в наборе, в качестве такой меры берут среднее арифметическое квадратов отклонений. Эту величину называют дисперсией.

Определение.

Среднее арифметическое квадратов отклонений от среднего значения называется в статистике дисперсией набора чисел.

Пример 1.

Обратимся к таблице производства пшеницы (млн.тонн) в России. Вычислить дисперсию.

1. Найдем среднее арифмети-ческое производ-ства пшеницы

Среднее арифме-тическое равно 35,5 млн.тонн в год

Найдем отклонения от среднего

Найдем квадраты отклонений

Вычислим среднее значение квадратов отклонений

(29,16+0,36+77,44+72,25+20,25+1,00+132,25) :7=47,53. 47,53 - дисперсия

Пример 2.

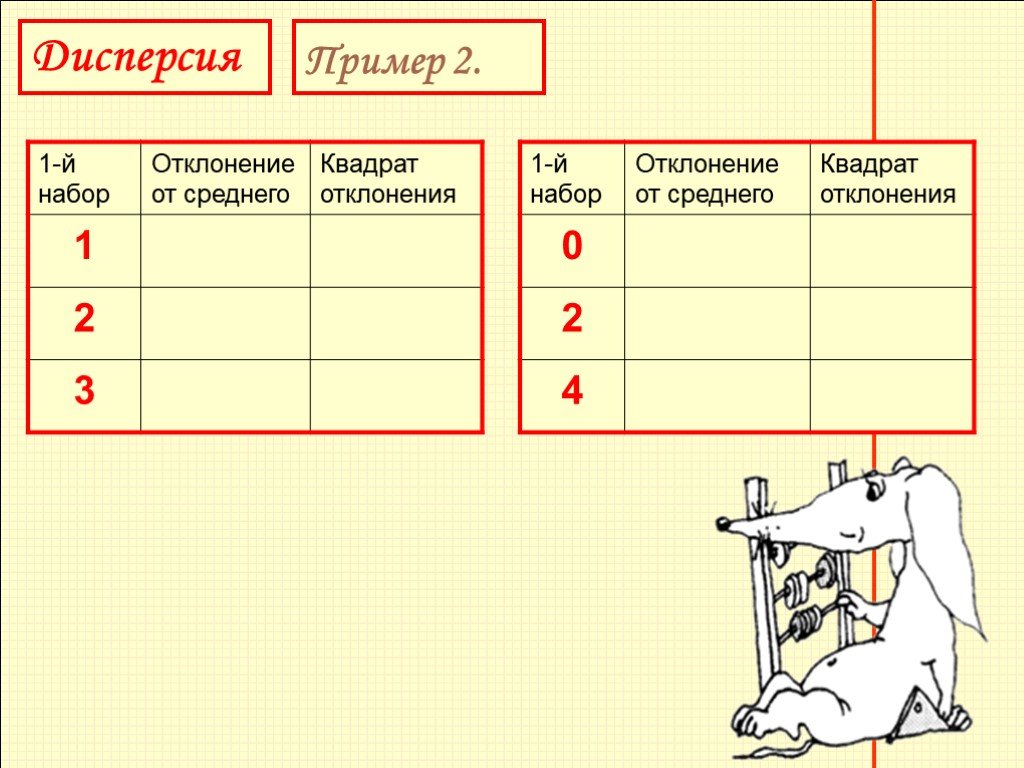
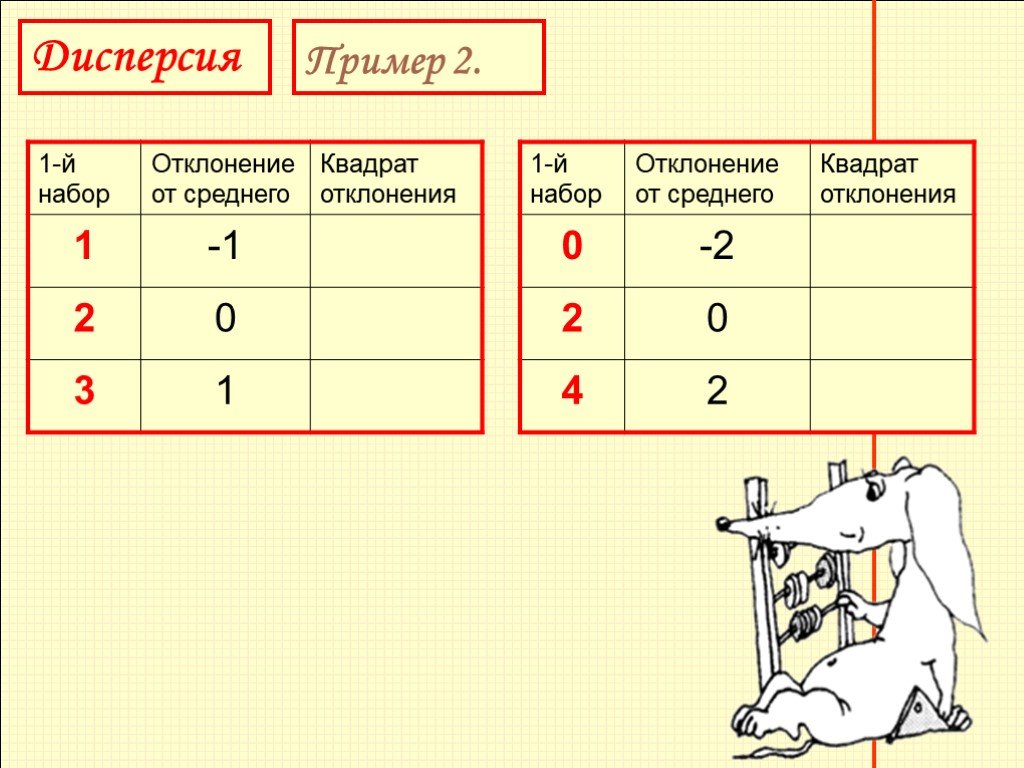
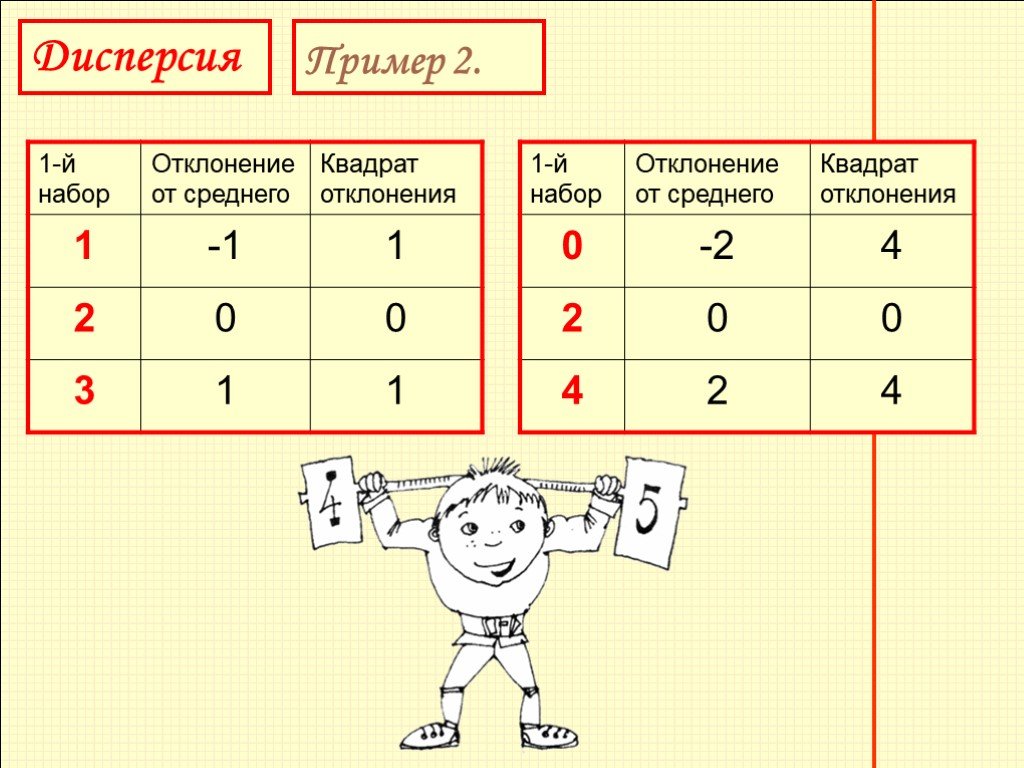
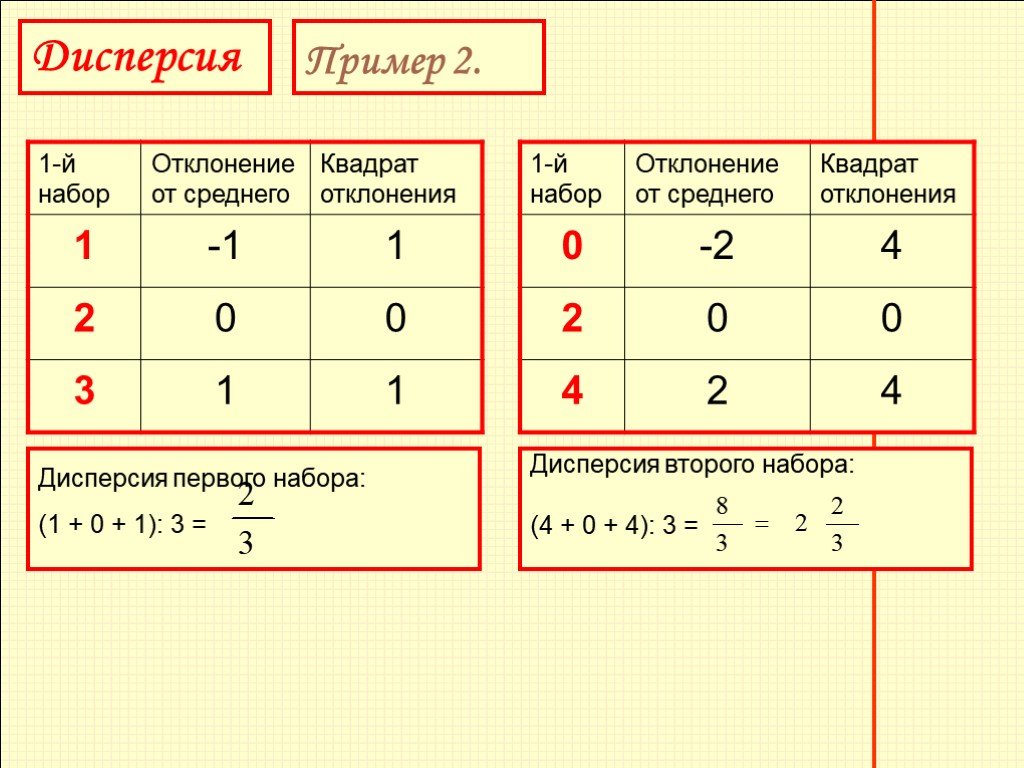
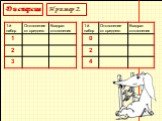
Покажем на простом примере, как дисперсия характеризует разброс отклонений. Возьмем два набора чисел 1, 2, 3 и 0, 2, 4. Среднее арифметическое значение обоих наборов равно 2. Для обоих наборов вычислим отклонения и квадраты отклонений и все данные занесем в таблицу 9.

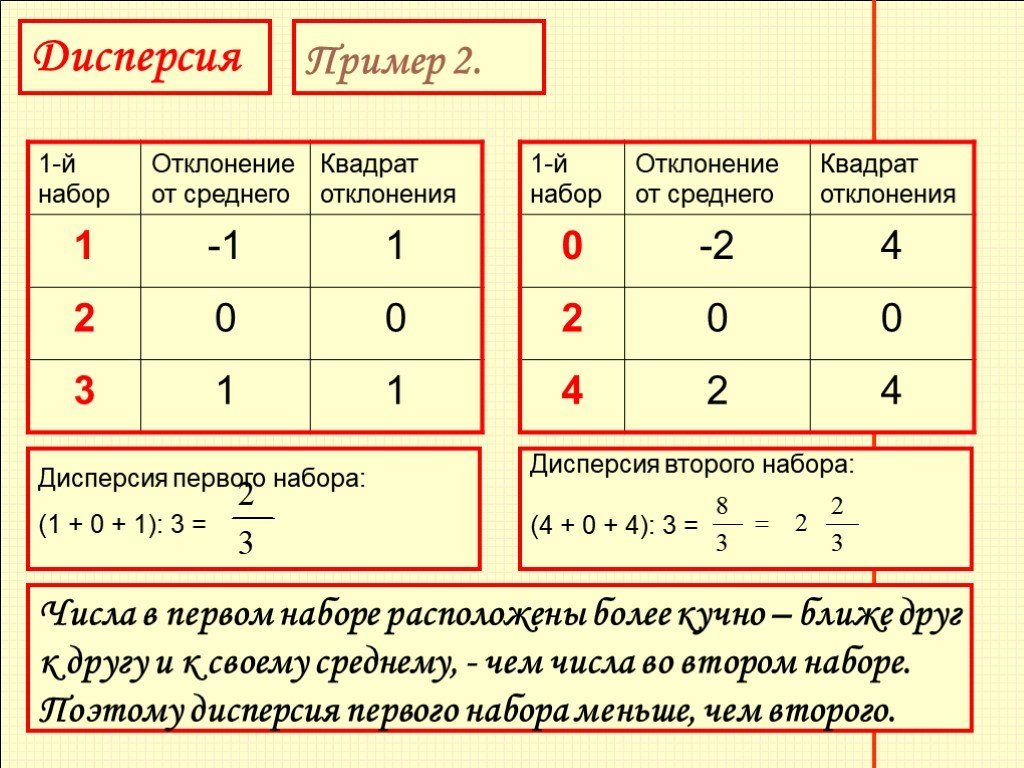
Дисперсия второго набора: (4 + 0 + 4): 3 =

Дисперсия первого набора: (1 + 0 + 1): 3 =

Числа в первом наборе расположены более кучно – ближе друг к другу и к своему среднему, - чем числа во втором наборе. Поэтому дисперсия первого набора меньше, чем второго.

Пример 3.

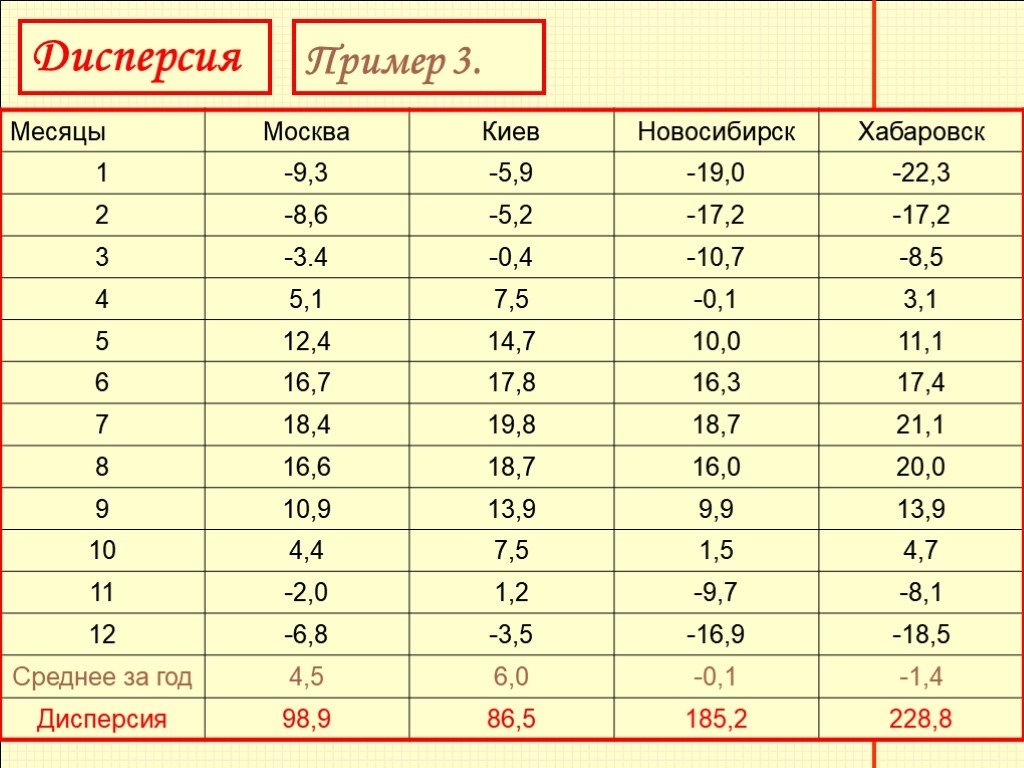
Континентальный климат отличается от умеренного более резкими изменениями температуры в течение года. В районах с континентальным климатом жаркое лето и очень холодная зима. С помощью дисперсии различия между двумя видами климата можно выразить количественно. Сравним для примера изменение температур в течение года в Москве и Киеве, где климат умеренный, с изменением температур в Новосибирске и Хабаровске, где климат континентальный. В таблице 10 приведены средние месячные температуры за 80 лет в Москве, Киеве, Новосибирске и Хабаровске.

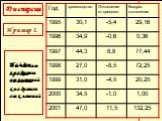
№1 Для данных чисел вычислите среднее значение. Составьте таблицу отклонений от среднего и квадратов отклонений от среднего и вычислите дисперсию: а) -1, 0, 4; в) -3, 1, 2, 4; д) -2, -1, 1, 2, 5; б) 2, 3, 7; г) 2, 6, 7, 5; е) -1, -3, -2, 3, 3.

№2. Даны два набора чисел. Отметьте их на числовой прямой. Вычислите дисперсию каждого из этих наборов. Дисперсия какого набора больше? а) 2, 3, 7 и 1, 2, 3; б) 2, 3, 4, 7 и 1, 5, 6, 8.

№3. Даны два набора чисел. Отметьте их на числовой прямой. Вычислите дисперсию каждого из этих наборов. Сравните дисперсии: а) 2, 3, 4 и 6, 7, 8; б) 3, 5, 7, 9 и 12, 14, 16, 18.

Обозначения и формулы

Числа в наборах часто приходиться обозначать буквами, подобно тому, как это делается при решении задач на движение. Но поскольку чисел может быть много, использовать для каждого числа отдельную букву неудобно. Поэтому поступают иначе: используют одну и ту же букву с номером. Таким образом, можно рассматривать набор х1, х2, х3, х4, х5 или у1, у2, у3, у4, у5, у6 и т.п. Номера чисел называются индексами.

Среднее арифметическое чисел х1, х2, х3, х4, х5 принято обозначать через Например, среднее арифметическое пяти чисел запишется так:

Отклонения от среднего значения теперь запишутся так:

Разберем на примере набора х1, х2, х3, х4, как записывается в символьном виде дисперсия. Дисперсия равна среднему арифметическому квадратов отклонений этих чисел от среднего значения. Обозначают дисперсию обысно через S 2. Получается:

№1. Запишите с помощью букв набор чисел 17, 3, 6, 21, 15. Чему равно значение х2 в этом наборе? Чему равно значение х5 в этом наборе?

№2. Пусть а – некоторое число. Вычислите среднее арифметическое и дисперсию набора чисел: а) х1 = а +1, х2 = а +2, х3= а + 3; а) х1 = а +2, х2 = а +3, х3= а + 7.

Свойства среднего арифметического и дисперсии

Буквенные обозначения чисел в наборе и введенные обозначения для среднего арифметического и для дисперсии набора чисел позволяют легко записать некоторые их свойства. Для простоты записи сформулируем их для набора из пяти чисел. Эти правила верны для любого количества чисел в наборе.

Рассмотрим набор чисел х1, х2, х3, х4, х5. Пусть - его среднее арифметическое, а - дисперсия. Прибавим к каждому числу этого набора постоянное число а. Получим набор х1+а, х2+а, х3+а, х4+а, х5+а.

Свойство 1.

Среднее арифметическое набора х1+а, х2+а, х3+а, х4+а, х5+а равно

Свойство 2.

Дисперсия набора х1+а, х2+а, х3+а, х4+а, х5+а равна дисперсии набора х1, х2, х3, х4, х5.

Свойство 3.

Среднее арифметическое набора ах1, ах2, ах3, ах4, ах5 равно

Свойство 4.

Среднее арифметическое набора ах1, ах2, ах3, ах4, ах5 равна