Презентация "Движение" по математике – проект, доклад
Презентацию на тему "Движение" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 27 слайд(ов).
Слайды презентации
Список похожих презентаций
Умножение и деление десятичных дробей. Движение небесных тел
Расшифруйте слово. 1,2 ∙ 0,3 = 0,36 С 48,6 : 6 = 7,4 ∙ 0,5 = 8,1 23,5 : 10 = 126 ∙ 0,01 = 3,7 М К О 6,1 5,49 : 0,9 = К О С М О С. Проверьте. . Пояс ...Движение по воде
ПРОБЛЕМА:. Поиск путей вовлечения в деятельность на уроке каждого учащегося. ЦЕЛЬ: Создание условий для осознания и осмысления способов решения задач ...Движение фигур в стереометрии
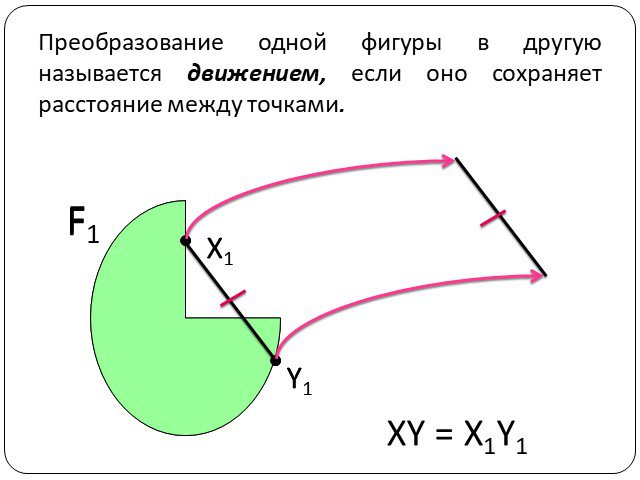
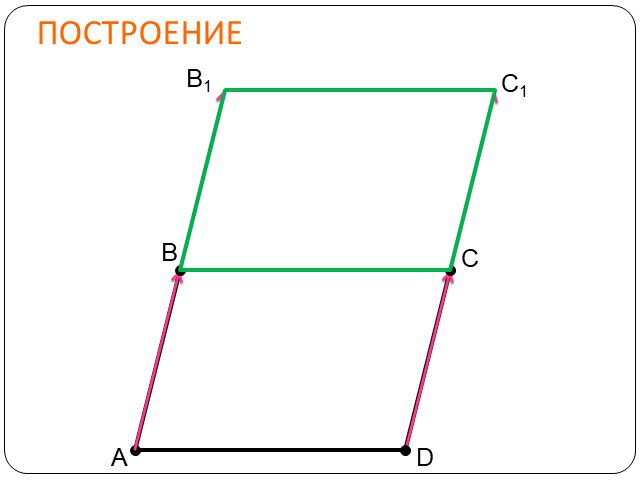
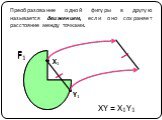
Движение – геометрическое преобразование, при котором сохраняются расстояния между точками. Движением (или перемещением) фигуры называется такое ее ...Движение и его виды
Начало движения. Задача По приглашению московские школьники в дни новогодних каникул посетят Англию. Найти кратчайшее расстояние от Москвы до Англии. ...Движение и сопряжение линий
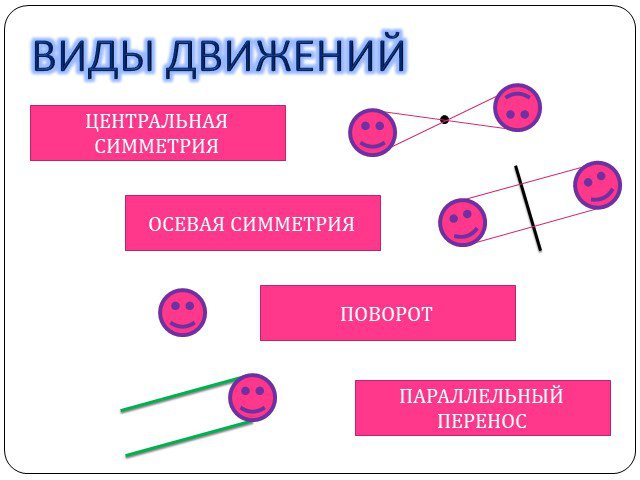
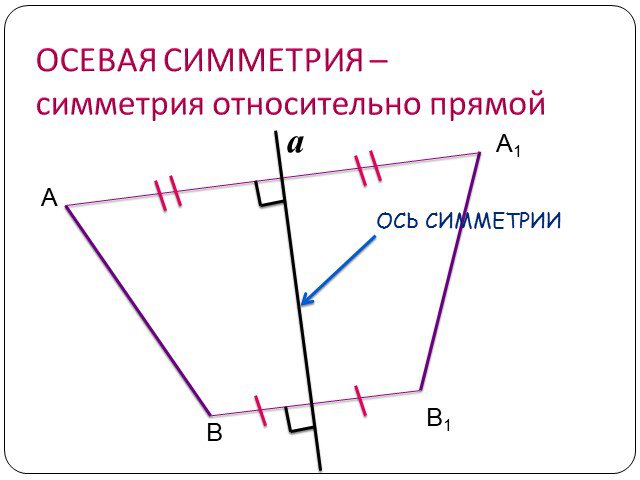
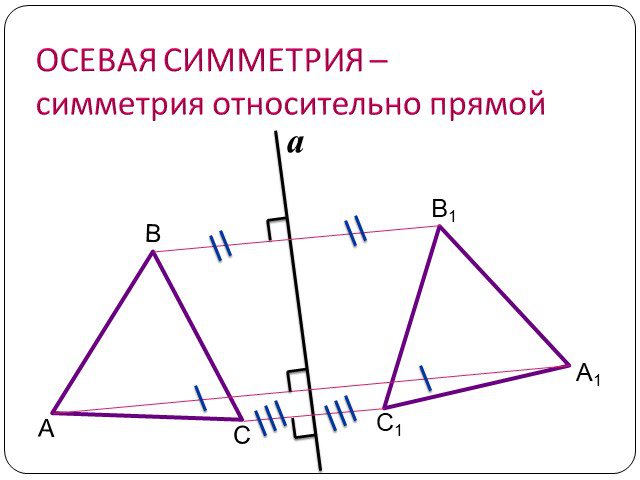
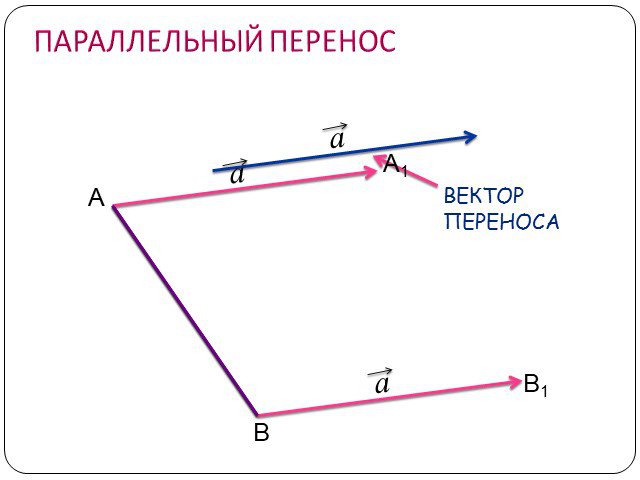
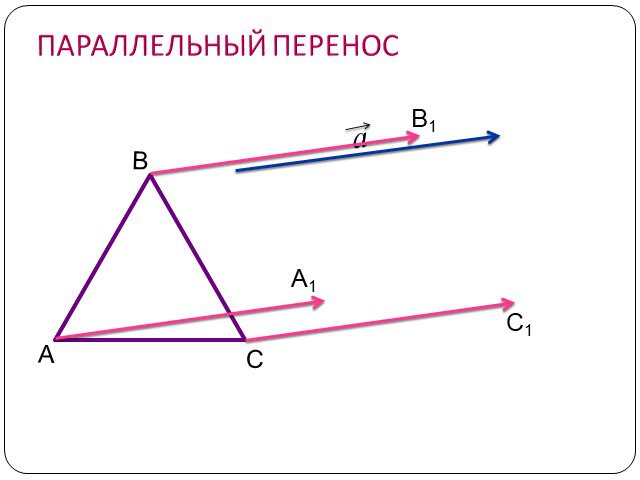
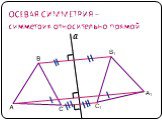
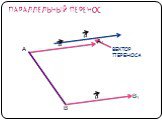
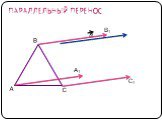
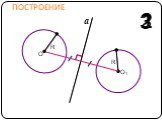
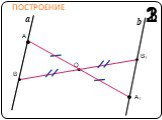
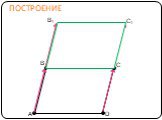
Содержание. Движение а) Отображение плоскости на себя б) Понятие движения в) Осевая симметрия г) Параллельный перенос Сопряжение а) Понятие сопряжения ...Движение в геометрии
Что называется движением? В какую фигуру при движении переходит отрезок, угол и др.? Назовите примеры движения. К каких науках применяется движение? ...Движение
Задание 1. Движения двух тел заданы уравнениями x1=12t, x2=120-10t. Найти место и время встречи этих тел, построить график зависимости координат от ...Движение
Отображение плоскости на себя. Любая точка плоскости оказывается сопоставленной некоторой точке. Движение плоскости – это отображение плоскости на ...Движение
Фигуру F называют прообразом фигуры F'. Преобразование фигуры, которое сохраняет расстояние между точками, называется движением этой фигуры. Свойства ...Движение
Симметрия - в переводе с греческого означает "одинаковость в расположении частей, пропорциональность", "гармония", "красота". . . . . . . . . . . ...Конспекты
Урок закрепление. Движение вдогонку
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа №3 г. Козьмодемьянска». Республики Марий Эл. ...Движение в противоположных направлениях
. Сценарий урока с использованием системно-деятельностного подхода в начальной школе. Урока математики в 4 классе. Движение в ...Движение в противоположных направлениях
Урок 27. Тип урока:. ОНЗ. Тема: «Движение в противоположных направлениях». Основные цели:. 1) формировать у учащихся умение проводить исследования ...Движение в одном направлении
Тема: «Движение в одном направлении». Цель урока: . познакомить учащихся с новым видом задач на движение (вдогонку). Задачи:. обучающие: . учиться ...Движение
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №30 им. Н.Н. Колокольцова». Кемеровской области Калтанского ...Движение
УРОК ГЕОМЕТРИИ В 8 КЛАССЕ на тему. «Движение». Методическая цель:. использование ИКТ в учебном процессе. Тип урока:. обобщающий. ...Движение
Урок математики для 5 класса по теме "Движение". . . . . . Математика 5 класс. 07.03.2012, 23:41. . • проверка знаний, повторение, ...Движение
Урок геометрии в 11 классе. Тема урока «Движение». Цель урока: повторить тему «Движение», рассматриваемую в планиметрии, подготовка к контрольной ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Содержит:27 слайд(ов)
Поделись с друзьями:
Скачать презентацию