Презентация "Площадь многоугольников" по математике – проект, доклад
Презентацию на тему "Площадь многоугольников" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 7 слайд(ов).
Слайды презентации
Список похожих презентаций
Площадь многоугольников
Проверка знаний Заштриховать квадраты, в которых указаны неверные утверждения. Пифагор и его теорема. Найдите правильную формулировку теоремы Пифагора: ...Площадь многоугольников
Чему равна площадь квадрата? Чему равна площадь прямоугольника? а b. запишите формулу площади треугольника. найдите площадь трапеции и запишите эту ...Площадь многоугольников
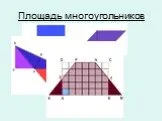
Многоугольник A B C D K L M N параллелограмм трапеция J B I P R. A D Z X H Y M N K T прямоугольник ромб квадрат. ПЛОЩАДЬ ТРАПЕЦИИ. Площадь трапеции ...Площадь трапеции
Трапеция. ВС параллельна АД, АВ не параллельна СД МN – средняя линия трапеции MN параллельна АД и СД АС и ВД - диагонали трапеции Если АВ=СД, то трапеция ...Площадь трапеции
Игра «Угадай формулу». Площадь трапеции равна произведению полусуммы её оснований на высоту. H H1. Дано: ABCD – трапеция AD и BC основания, BH – высота ...Площадь прямоугольного треугольника
А В С D 12 дм 6 дм 12 · 6 = 72 (дм²) S□ = a · b S□ -? SΔ -? (12 · 6) : 2 = 36 (дм²) SΔ = (a · b ) : 2 Шаг 1. Шаг 1* (трудный). 10 дм 16 дм Шаг 2. ...Площадь прямоугольника: практикум
СРЕДИ ФИГУР, ПРИВЕДЕННЫХ НА РИСУНКЕ, УКАЖИТЕ:. а). равные фигуры б). фигуры равной площади. А Б В Г. в). площадь каждой фигуры. Чему равна площадь ...Длина окружности. Площадь круга. Коллекция задач для 6 класса
. Великий древнегреческий математик Архимед (III в. до н.э.), выполнив множество измерений, установил, что длина окружности примерно в раза больше ...Нахождение площадей многоугольников
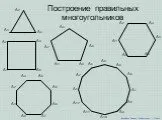
Математика, друзья, Абсолютно всем нужна. На уроке работай старательно, И успех тебя ждет обязательно! S=ab S=a·a. Тема урока: «Нахождение площадей ...Построение правильных многоугольников
В заданиях на построение используются: карандаш, линейка(для проведения прямых, лучей и отрезков) и циркуль(для построения окружностей и дуг). I. ...Круг. Площадь круга
Ну-ка, проверь дружок, Ты готов начать урок? Всё ль на месте, Всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? Все ль внимательно ...Многообразие многоугольников
Великий и непредсказуемый Пифагор. Карл Гаусс, учащийся первого курса Геттингенского университета, решил задачу, перед которой математическая наука ...Интеграл. Площадь криволинейной трапеции»
x. Различные виды криволинейных трапеций. Площадь криволинейной трапеции. Найти площадь криволинейной трапеции, ограниченной : графиком функции f(x) ...Интеграл. Площадь криволинейной трапеции
Цели и задачи урока: Обобщить и систематизировать теоретический материал по теме. Отработать навыки вычисления первообразных для функций. Отработать ...Длина окружности. Площадь круга. Практические применения
Цели развивающие: Активизировать деятельность учащихся через разнообразные виды самостоятельной работы. Способствовать развитию долговременной памяти ...Площадь треугольника
Устная работа. А В С D 6 см 10 см К. ABCD – параллелограмм. Найти площадь параллелограмма. 5 см 8 см. Теорема о площади треугольника. Дано: ABD – ...Объем шара. Площадь сферы
Внешний диаметр полого шара равен 18 см, а толщина стенок - 3 см. Найдите объем материала, из которого сделан шар. №1. Внутренний диаметр полого шара ...Площадь фигуры
Старая сказка на новый лад. Сказка - умница и прелесть, с нами рядышком жив ёт... Сосчитай, разгадай! 97 - 89 = 36 : 6 = 53 - 48 = 42 : 6 = 12 : 4 ...Площадь параллелограмма
Пример 1. Стороны параллелограмма равны 15 см и 9 см. Высота, опущенная на первую сторону, равна 6 см. Найдите высоту, опущенную на вторую сторону ...Длина окружности. Площадь круга
Устный счёт 500+310 :90 *60 -120 :14 910:13 *8 -80 :160 *350. Отрезки А В С К Круг Цилиндр Окружность Окружность, круг. В С А. Окружность - это замкнутая ...Конспекты
Площадь многоугольников
Открытый урок геометрии в 8 классе. Тема: Площадь многоугольников. Цель:. повторить, закрепить, обобщить и систематизировать знания учащихся по ...Площадь многоугольников
Министерство образования Саратовской области. Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа с.Вязовка». Татищевского ...Площадь сложной фигуры
5-й класс. Математика. Урок «Площадь сложной фигуры». Вовденко. . Ольга. . Леонидовна. , учитель математики. . МБОУ СОШ № 61 имени М.И. Неделина ...Длина окружности. Площадь круга. Шар
Урок № 33. Тема. :. Длина окружности. . Площадь круга. Шар. ЦЕЛЬ:. . Дидактическая. Учащиеся должны научиться:. - Вычислять длину окружности;. ...Площадь прямоугольного треугольника
Муниципальное бюджетное общеобразовательное учреждение. гимназия №19 имени Поповичевой Н.З. г. Липецка. Конспект урока по ...Построение правильных и полуправильных многоугольников
МКОУ В(С)ОШ № 2 ст. Александрийской. Георгиевского района. Ставропольского края. Урок в 10 классе по теме:. "Построение правильных и полуправильных ...Площадь прямоугольника
Разработка урока-открытия по теме: «Площадь прямоугольника». учителя начальных классов, МАОУ «ГИМНАЗИЯ №1», г. Салехард,. . Кантарбаева Маргарита ...Площадь треугольника
Конспект урока по математике в 5 ом классе (базовый уровень). Тема урока:. Площадь треугольника. Цели урока:. . познакомить учащихся с площадью ...Площадь фигур
ГОУ ЦО «Школа здоровья» № 1099 г. Москва. Открытый урок в игровой форме (деловая игра). Тема: площади фигур. Учитель: Тюльнева Светлана Викторовна. ...Площадь
ФИО:. Лукоянова Ольга Александровна. Место работы:. МКОУ СОШ №18 г. Асбест. Должность:. Учитель математики. Тема:. . Площадь. Формула площади ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:11 июня 2019
Категория:Математика
Содержит:7 слайд(ов)
Поделись с друзьями:
Скачать презентацию