Презентация "Решение задач на повторение" по математике – проект, доклад
Презентацию на тему "Решение задач на повторение" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 27 слайд(ов).
Слайды презентации
Список похожих презентаций
Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
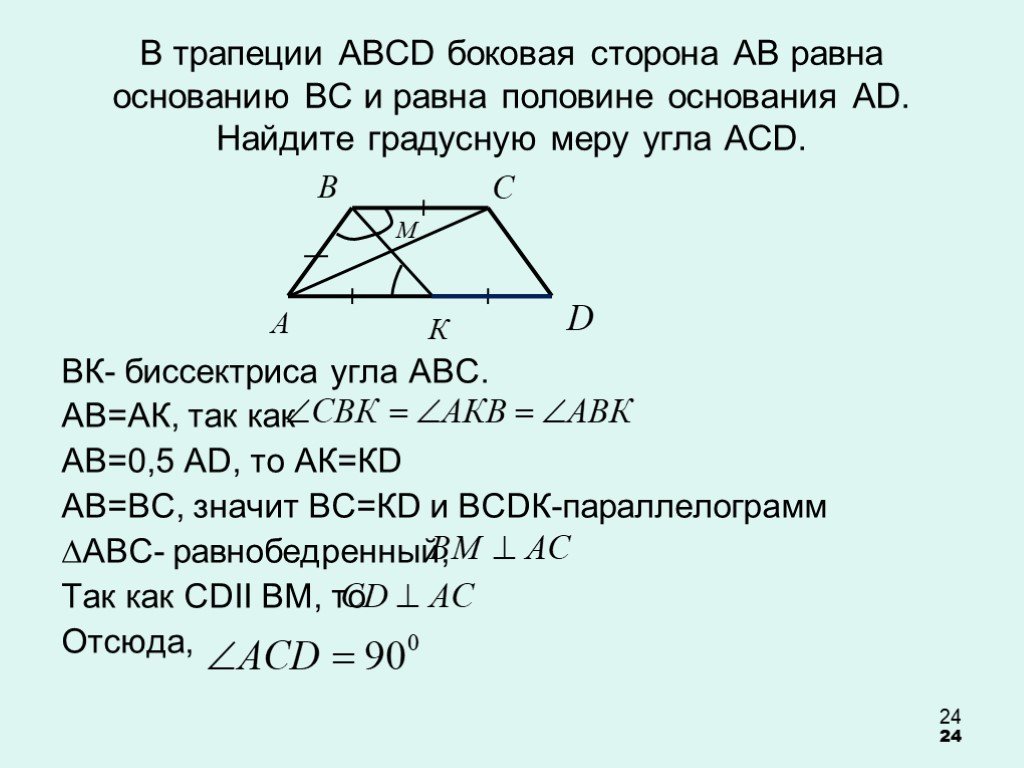
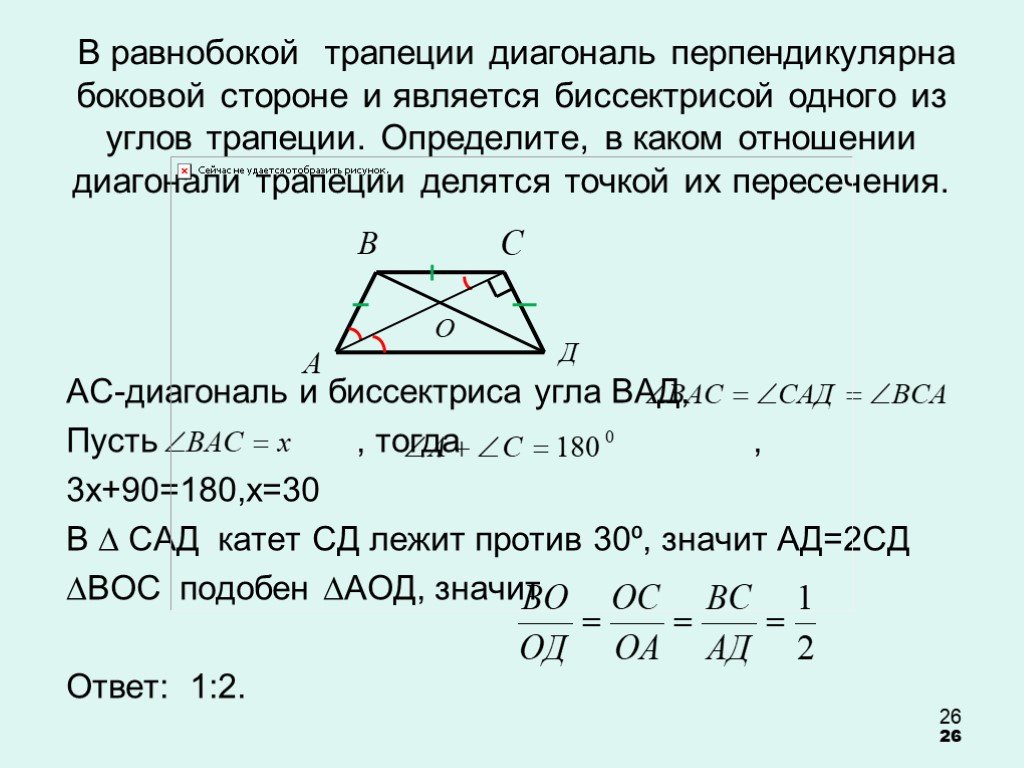
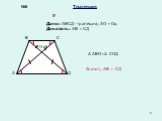
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...«Моя математика» - задачи на нахождение целого или части
МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ...Алггоритм. Решение задач
Задача 1. В урне хранится некоторое количество чёрных и белых шаров. Требуется разложить эти шары по двум корзинам чёрного и белого цвета: белые шары ...Вектор решение задач
Выразить векторы AM, DA, CA, MB, CD через вектор a и вектор b. № 1 Выразить векторы ВС, CD, AC, OC, OA через векторы а и b. Тивякова Л.А. № 2 Выразить ...«Задачи на проценты»
Тема урока: Проценты. Тип урока: урок обобщения и систематизации знаний. Цели урока: Образовательные: Обобщение и систематизация знаний учащихся о ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Арифметика Л.Ф. Магницкого. Задачи на сплавы и смеси
Цели моей работы. Познакомиться с биографией Леонтия Филипповича Магницкого Научиться решать задачи на сплавы, находить процентное содержание веществ ...Бинарный урок математики и природоведения по теме "Итоговое повторение"
Итоговое повторение. Ну-ка, проверь дружок, Ты готов начать урок? Всё ль на месте, Всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Влияние "главных чисел" на характер человека
Эпиграф. Мысль выражать все числа знаками настолько проста, что именно из – за этой простоты сложно осознать, сколь она удивительна. Пьер Симон Лаплас. ...3 вида разложение многочлена на множители
1 вид вынесение общего множителя за скобки. Что значит разложить многочлен на множители? Разложить многочлен на множители — это значит представить ...Блиц-опрос "Решение треугольников"
Выбери вопрос. В треугольнике АВС угол А равен 40 градусов. Внешний угол при вершине В равен 68 градусов. Найдите угол С. Угол С равен 28 градусов. ..."Разрезание геометрических фигур на части"
ЗАДАЧИ НА РАЗРЕЗАНИЯ. Теорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат. ...Арксинус. Решение уравнения sin t = a
Цели. Изучить определение арксинуса числа. Изучить формулы решения простейшего тригонометрического уравнения sin t = a. Повторим. Что называется синусом ...Аксиомы расположения точек на прямой и плоскости
Выполните действия и сделайте записи:. 1. Изобразите точку С, лежащую на прямой а. 2. Изобразите точку D, не лежащую на этой прямой. 3. Проведите ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Конспекты
Деление двузначного числа на однозначное и двузначное число, деление чисел с остатком, решение задач
. ТЕМА: «. Деление двузначного числа на однозначное и двузначное число, деление чисел с остатком, решение задач». . Сухова Т.А. . ...Деление двузначного числа на однозначное. Решение арифметических задач
. УРОК 15 (задания 87-93). . . Учебный предмет:. математика. Класс:. 3. . Авторы учебника:. . Истомина Н.Б., Редько З.Б., Иванова И.Ю. УМК ...Действия с величинами. Соотношение цены, количества, стоимости. Решение задач, выражений
Автор: Енина Н.В. учитель начальных классов МКОУ НОШ №17 ст.Зольской,. . Ставропольский край. . Урок математики в 3-м классе. УМК «Гармония». ...Две основные задачи на дроби
. Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 8». Методическая разработка урока математики . ...Геометрическое решение негеометрических задач
Урок по теме:. «Геометрическое решение негеометрических задач». Сивак Светлана Олеговна. учитель математики. высшей категории. Гимназии №56. ...Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Действия с обыкновенными дробями. Основные задачи на дроби
ГБС(К)ОУ ШИ. I. -. II. вида г. Тихорецка Краснодарского края. Урок – КВН. в 7 классе по теме:. «Действия с обыкновенными дробями. Основные ...Действия с составными именованными числами. Решение задач различного вида
Урок математики в 4 классе. . По программе «Школа 2100». Тема урока:. “Действия с составными именованными числами. Решение задач различного вида. ...Вычитание из чисел 8, 9. Решение задач
КРАСНОПАХАРЕВСКАЯ ООШ – ФИЛИАЛ МБОУ «НОВАДЕЖДИНСКАЯ СОШ». Урок математики для 1 класса по теме: «Вычитание из чисел 8, 9. Решение задач». . Автор: ...Деление двузначного числа на двузначное способом подбора
Тема урока Деление двузначного числа на двузначное способом подбора. Цель урока:. формировать умение выполнять деление двузначного числа на двузначное; ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 июня 2019
Категория:Математика
Содержит:27 слайд(ов)
Поделись с друзьями:
Скачать презентацию