Презентация "лобачевский" по математике – проект, доклад

Геометрия Лобачевского

Лекцию разработал доцент кафедры общей физики Чувашского государственного университета Г.М. Сорокин

СОДЕРЖАНИЕ 1. ВВЕДЕНИЕ 2. МОДЕЛИ 2.1 ПСЕВДОСФЕРА 2.2 МОДЕЛЬ КЛЕЙНА 2.3 МОДЕЛЬ ПУАНКАРЕ 2.4 ПОВЕРХНОСТЬ ПОСТОЯННОЙ ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ 3. СОДЕРЖАНИЕ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО 4. ПРИЛОЖЕНИЯ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО 5. НЕЕВКЛИДОВА ГЕОМЕТРИЯ

1. ВВЕДЕНИЕ Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. Евклидова аксиома о параллельных гласит: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её В геометрии Лобачевского, вместо неё принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии и математики вообще. Источником геометрии Лобачевского послужил вопрос об аксиоме о параллельных, которая известна также как V постулат Евклида (под этим номером утверждение, эквивалентное приведённой выше аксиоме о параллельных, фигурирует в списке постулатов в «Началах» Евклида). Этот постулат, ввиду его сложности в сравнении с другими, вызвал попытки дать его доказательство на основании остальных постулатов. Вот перечень учёных, занимавшихся доказательством V постулата до 19 в.: - древнегреческий математики Птолемей (II в.), Прокл (V в.) (основано на предположении о конечности расстояния между двух параллельными);

- Ибн аль-Хайсам из Ирака (конец X — начало XI вв.) (пытался доказать V постулат, исходя из предположения, что конец движущегося перпендикуляра к прямой описывает прямую линию); - иранский математик Омар Хайям (2-я половина XI — начало XII вв.); - азербайджанский математик Насирэддин Туси (XIII в.) (при доказательстве V постулата исходили из предположения, что две сходящиеся прямые не могут при продолжении стать расходящимися без пересечения); - немецкий математик К. Клавий (1574), - итальянские математики: П. Катальди (впервые в 1603 напечатавший работу, целиком посвященную вопросу о параллельных), Дж. Борелли (1658), Дж. Витале (1680); - английский математик Дж. Валлис (1663, опубликовано в 1693) (основывает доказательство V постулата на предположении, что для всякой фигуры существует ей подобная, но не равная фигура). Доказательства перечисленных выше геометров сводились к замене V постулата другими предположением, казавшимся более очевидным. *Итальянский математик Дж. Саккери (1733) сделал попытку доказать V постулат от противного. Приняв предложение, противоречащее постулату Евклида, Саккери развил из него довольно обширные следствия. Ошибочно признав некоторые из этих следствий приводящими к противоречиям, Саккери заключил, что постулат Евклида доказан. Немецкий математик И. Ламберт (около 1766, опубликовано в 1786) предпринял аналогичные исследования, однако он не повторил ошибки Саккери, а признал своё бессилие обнаружить в построенной им системе логическое противоречие. Попытки доказательства постулата предпринимались и в XIX веке. Французский математик А. Лежандра; одно из его доказательств (1800) основано на допущении, что через каждую точку внутри острого угла можно

провести прямую, пересекающую обе стороны угла, то есть, как и все его предшественники, он заменил постулат др. допущением. Довольно близко к построению геометрии Лобачевского подошли немецкие математики Ф. Швейкарт (1818) и Ф. Тауринус (1825), однако ясно выраженной мысли о том, что намечаемая ими теория будет логически столь же совершенна, как и геометрия Евклида, они не имели. Вопрос о V постулате Евклида, занимавший геометров более двух тысячелетий, был решен Лобачевским. Это решение сводится к тому, что постулат не может быть доказан на основе других посылок евклидовой геометрии и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий. Лобачевский сделал об этом сообщение в 1826, а в 1829—30 напечатал работу «О началах геометрии» с изложением своей теории. Ранее независимо от него и друг от друга к аналогичным выводам приходили Карл Фридрих Гаусс и Янош Бойяи, но их труды не получили своевременной известности. Гаусс воздерживался от публикаций, сохранилось лишь письмо; Бойяи, выступил лишь в 1832, вскоре, разочаровавшись в своем “опоздании в открытии доказательства”, оставил тему. Лобачевский выступил как первый, наиболее яркий и последовательный пропагандист этой теории. Хотя геометрия Лобачевского развивалась как умозрительная теория и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно Лобачевский рассматривал её не как игру ума, а как возможную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации и тем полностью решен вопрос о её реальном смысле, логической непротиворечивости.

2. МОДЕЛИ Модели геометрии Лобачевского дали доказательство её непротиворечивости, точнее показали что геометрия Лобачевского столь же непротиворечива, как геометрия Евклида. Сам Лобачевский дал основы своей аналитической геометрии, и тем самым он уже фактически наметил такую модель. Он также заметил что орисфера в пространстве Лобачевкого изометрична евклидовой плоскости, тем самым фактически предложил обратную модель. Тем не менее, само понятие о модели прояснилось в работах Клейна и других. 2.1 ПСЕВДОСФЕРА Итальянский математик Э. Бельтрами в 1868 заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере. Однако здесь даётся интерпретация только геометрии только локально, т.е. на куске, а не на всей плоскости Лобачевского.

2.2 МОДЕЛЬ КЛЕЙНА

В 1871 Клейн предложил первую полноценную модель плоскости Лобачевского. Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга,

переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского. Иными словами, всякое утверждение геометрии Лобачевского на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь явно не выполняется, так как через точку O, не лежащую на данной хорде а (то есть «прямой»), проходит сколько угодно не пересекающих её хорд («прямых») (например, b, b'). В этой модели расстояние между точками (см. рисунок) определяется как угол — ещё сложнее.

2.3 МОДЕЛЬ ПУАНКАРЕ

Позже Пуанкаре, в связи с задачами теории функций комплексного переменного дал другую модель. За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми. Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.

2.4 ПОВЕРХНОСТЬ ПОСТОЯННОЙ ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ Другое аналитическое определение геометрии Лобачевского состоит в том, что геометрия Лобачевского определяется как геометрия риманова пространства постоянной отрицательной кривизны. Это определение было фактически дано ещё в 1854 Риманом и включало модель геометрии Лобачевского как геометрии на поверхностях постоянной кривизны. Однако Риман не связал прямо своих построений с геометрией Лобачевского, а его доклад, в котором он о них сообщил, не был понят и был опубликован лишь после его смерти (в 1868).

3. СОДЕРЖАНИЕ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО Содержание геометрии Лобачевского. Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, т. к. именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, общи обеим геометриям и образуют т. н. абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие отделы, включая тригонометрию и начала аналитической и дифференциальной геометрии. Приведём несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским. 1) В геометрии Лобачевского не существует подобных, но неравных треугольников; треугольники равны, если их углы равны. Поэтому существует абсолютная единица длины, т. е. отрезок, выделенный по своим свойствам, подобно тому как прямой угол выделен своими свойствами. Таким отрезком может служить, например, сторона правильного треугольника с данной суммой углов. 2) Сумма углов всякого треугольника меньше p и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность p — (a + b + g), где a, b, g — углы треугольника, пропорциональна его площади. 3) Через точку О, не лежащую на данной прямой а, проходит бесконечно много прямых, не пересекающих а и находящихся с ней в одной плоскости; среди них есть две крайние b, b', которые и называются параллельными прямой а в смысле Лобачевского. В моделях Клейна (Пуанкаре) они

изображаются хордами (дугами окружностей), имеющими с хордой (дугой) а общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек) (рис. 1,3). Угол ее между прямой b (или b') и перпендикуляром из О на а — т. н. угол параллельности — по мере удаления точки О от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель b с одной стороны (а b' с противоположной) асимптотически приближается к а, а с другой — бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден). 4) Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой. 5) Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом. 6) Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом. 7) Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии. 8) Длина окружности не пропорциональна радиусу, а растет быстрее.

9) Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от p; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2p, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского. переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского. Геометрии Лобачевского продолжает разрабатываться многими геометрами; в ней изучаются: решение задач на построение, многогранники, правильные системы фигур, общая теория кривых и поверхностей и т. п. Ряд геометров развивали также механику в пространстве Лобачевского. Эти исследования не нашли непосредственных применений в механике, но дали начало плодотворным геометрическим идеям. В целом геометрии Лобачевского. является обширной областью исследования, подобно геометрии Евклида.

4. ПРИЛОЖЕНИЯ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО

Сам Лобачевский применил свою геометрию к вычислению определённых интегралов. В теории функций комплексного переменного геометрия Лобачевского помогла построить теорию автоморфных функций. Связь с геометрией Лобачевского была здесь отправным пунктом исследований Пуанкаре, который писал, что «неевклидова геометрия есть ключ к решению всей задачи». Геометрия Лобачевского находит применение также в теории чисел, в её геометрических методах, объединённых под названием «геометрия чисел». Была установлена тесная связь геометрии Лобачевского с кинематикой специальной (частной) теории относительности. Эта связь основана на том, что равенство, выражающее закон распространения света при делении на t², то есть для скорости света, даёт — уравнение сферы в пространстве с координатами vx, vy, vz — составляющими скорости по осям х, у, z (в «пространстве скоростей»). Преобразования Лоренца сохраняют эту сферу и, так как они линейны, переводят прямые пространства скоростей в прямые. Следовательно, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса с, то есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского. Замечательное приложение геометрии Лобачевского нашла в общей теории относительности. Если считать распределение масс материи во Вселенной равномерным (это приближение в космических масштабах допустимо), то оказывается, что при определённых условиях пространство имеет геометрию Лобачевского. Т. о., предположение Лобачевского о его геометрии как возможной теории реального пространства оправдалось.

5. НЕЕВКЛИДОВА ГЕОМЕТРИЯ

Среди аксиом Евклида была аксиома о параллельности прямых, а точнее, пятый постулат о параллельных линиях: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. В современной формулировке она говорит о существовании не более одной прямой, проходящей через данную точку вне данной прямой и параллельной этой данной прямой. Сложность формулировки пятого постулата породила мысль о возможной зависимости его от других постулатов, и потому возникали попытки вывести его из остальных предпосылок геометрии. Как правило, это заканчивалось неудачей. Были попытки доказательства от противного: прийти к противоречию, предполагая верным отрицание постулата. Однако и этот путь был безуспешным. Наконец, в начале XX века почти одновременно сразу у нескольких математиков: у К. Гаусса в Германии, у Я. Больяи в Венгрии и у Н. Лобачевского в России возникла мысль о существовании геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную. В силу приоритета Н. Лобачевского, который первым выступил с этой идеей в 1826, и его вклада в развитие новой, отличной от евклидовой геометрии последняя была названа в его честь «геометрией Лобачевского». Аксиоматика планиметрии Лобачевского отличается от аксиоматики планиметрии Евклида лишь одной аксиомой: аксиома параллельности заменяется на ее отрицание – аксиому параллельности Лобачевского Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a. Непротиворечивость системы аксиом доказывается представлением модели, в которой реализуются данные аксиомы. Модель планиметрии Лобачевского

на евклидовой плоскости, которая будет здесь представлена, сделана по материалам учебника «Геометрия» (А. Д. Александров, А. Л. Вернар, В. И. Рыжик, М: Просвещение, 1991). Эта модель была предложена французским математиком Анри Пуанкаре в 1882 году. Для начала напомним основные понятия и аксиоматику, на которой базировалось изложение, систематизировав их заново и дополнив необходимыми аксиомами. За основные объекты были приняты точка, прямая и фигура. За основные отношения между этими объектами принимаются: 1) точка принадлежит фигуре, в частности прямой; 2) точка лежит между двумя точками для точек прямой. Следующие определения базируются на основных определениях. Фигура называется объединением некоторых данных фигур, если ей принадлежат все точки этих фигур, и никакие другие. Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками. Эти точки называются концами отрезка. Лучом AB называется часть прямой, состоящая из всех ее точек, лежащих по ту же сторону от точки A, что и точка B. Точка A называется вершиной луча. Углом называется фигура, которая состоит из точки – вершины угла и двух различных лучей, исходящих из этой точки, – сторон угла. Полуплоскостью, ограниченной прямой a, называется фигура, обладающая следующими свойствами: Она не содержит прямую а; Если точки A и B принадлежат полуплоскости, то отрезок AB не имеет общих точек с а; Если же A принадлежит полуплоскости, а B нет, то отрезок AB имеет общую точку с прямой а; Приведем систему аксиом, обозначив римской цифрой номер группы, а арабской – номер аксиомы в группе.

I. АКСИОМЫ СВЯЗИ ПРЯМОЙ И ТОЧКИ. Существуют, по крайней мере, две точки. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую и только одну. Из трех точек на прямой одна и только одна лежит между двумя другими. II. МЕТРИЧЕСКИЕ АКСИОМЫ ОТРЕЗКА. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой. На каждом луче от его начала можно отложить отрезок заданной длины и только один. III. АКСИОМА НЕПРЕРЫВНОСТИ. Пусть A и B – любые две точки прямой a и пусть и – совокупности всех точек отрезка AB, таких, что и любая точка из лежит по ту же сторону, что и точка A от любой точки из Тогда существует точка C, такая, что любая точка из лежит по ту же сторону от C, что и A, а любая точка из – по ту же сторону от C, что и B.

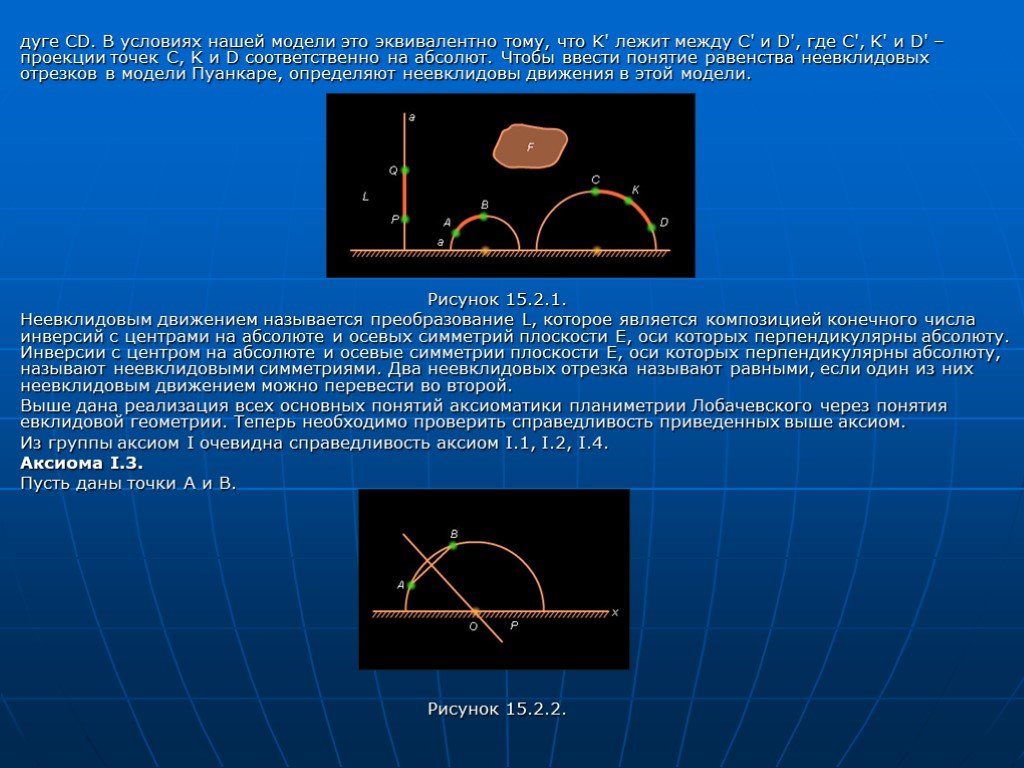
IV. АКСИОМЫ ПЛОСКОСТИ. Прямая разбивает плоскость на две полуплоскости. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. От любого луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данного луча. V. АКСИОМА ПАРАЛЛЕЛЬНОСТИ ЕВКЛИДА. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной. Построение модели Пуанкаре начнем с того, что придадим конкретный смысл основным объектам и основным отношениям планиметрии Лобачевского. Для этого фиксируем на евклидовской плоскости E горизонтальную прямую x. Она носит название «абсолюта». Точками плоскости Лобачевского считаются точки плоскости E, лежащие выше абсолюта x. Таким образом, в модели Пуанкаре плоскость Лобачевского – это полуплоскость L, лежащая выше абсолюта. Прямыми плоскости L считаются полуокружности с центрами на абсолюте или лучи с вершинами на абсолюте и перпендикулярные ему. Фигура на плоскости Лобачевского – это фигура полуплоскости L. Принадлежность точки фигуре понимается так же, как и на евклидовой плоскости E. При этом отрезком плоскости L считается дуга окружности с центром на абсолюте или отрезок прямой, перпендикулярной абсолюту (см. рис. 15.2.1). Точка K лежит между точками C и D, значит, что K принадлежит

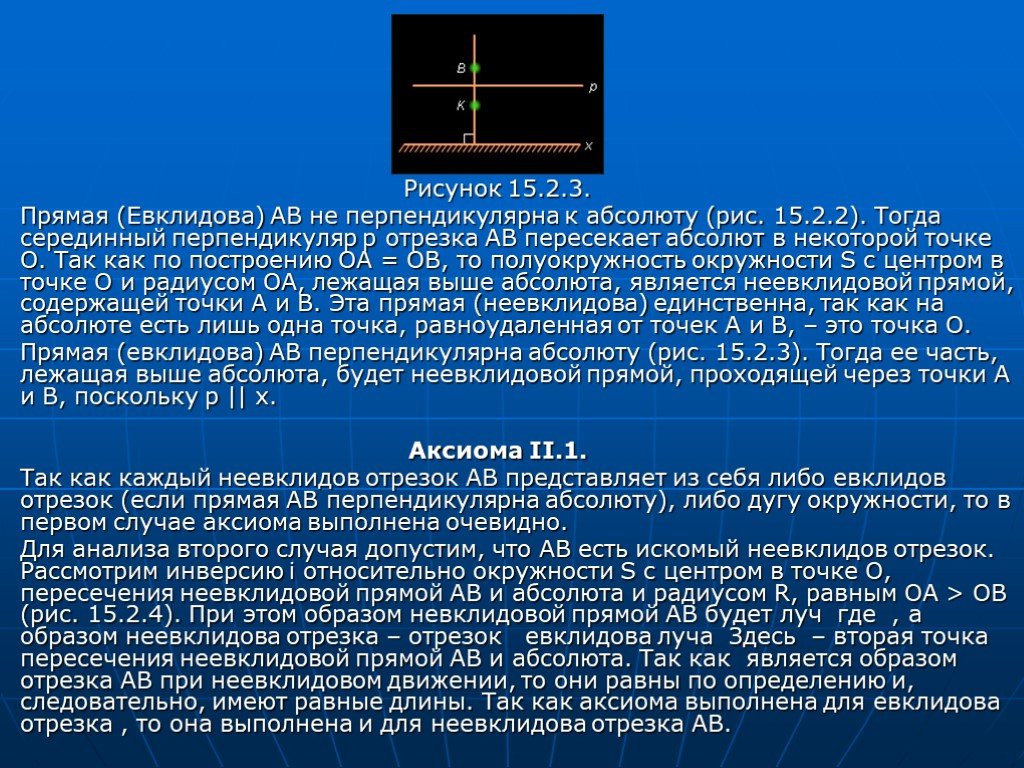
дуге CD. В условиях нашей модели это эквивалентно тому, что K' лежит между C' и D', где C', K' и D' – проекции точек C, K и D соответственно на абсолют. Чтобы ввести понятие равенства неевклидовых отрезков в модели Пуанкаре, определяют неевклидовы движения в этой модели. Рисунок 15.2.1. Неевклидовым движением называется преобразование L, которое является композицией конечного числа инверсий с центрами на абсолюте и осевых симметрий плоскости E, оси которых перпендикулярны абсолюту. Инверсии с центром на абсолюте и осевые симметрии плоскости E, оси которых перпендикулярны абсолюту, называют неевклидовыми симметриями. Два неевклидовых отрезка называют равными, если один из них неевклидовым движением можно перевести во второй. Выше дана реализация всех основных понятий аксиоматики планиметрии Лобачевского через понятия евклидовой геометрии. Теперь необходимо проверить справедливость приведенных выше аксиом. Из группы аксиом I очевидна справедливость аксиом I.1, I.2, I.4. Аксиома I.3. Пусть даны точки A и B. Рисунок 15.2.2.

Рисунок 15.2.3. Прямая (Евклидова) AB не перпендикулярна к абсолюту (рис. 15.2.2). Тогда серединный перпендикуляр p отрезка AB пересекает абсолют в некоторой точке O. Так как по построению OA = OB, то полуокружность окружности S с центром в точке O и радиусом OA, лежащая выше абсолюта, является неевклидовой прямой, содержащей точки A и B. Эта прямая (неевклидова) единственна, так как на абсолюте есть лишь одна точка, равноудаленная от точек A и B, – это точка O. Прямая (евклидова) AB перпендикулярна абсолюту (рис. 15.2.3). Тогда ее часть, лежащая выше абсолюта, будет неевклидовой прямой, проходящей через точки A и B, поскольку p || x. Аксиома II.1. Так как каждый неевклидов отрезок AB представляет из себя либо евклидов отрезок (если прямая AB перпендикулярна абсолюту), либо дугу окружности, то в первом случае аксиома выполнена очевидно. Для анализа второго случая допустим, что AB есть искомый неевклидов отрезок. Рассмотрим инверсию i относительно окружности S с центром в точке O, пересечения неевклидовой прямой AB и абсолюта и радиусом R, равным OA > OB (рис. 15.2.4). При этом образом невклидовой прямой AB будет луч где , а образом неевклидова отрезка – отрезок евклидова луча Здесь – вторая точка пересечения неевклидовой прямой AB и абсолюта. Так как является образом отрезка AB при неевклидовом движении, то они равны по определению и, следовательно, имеют равные длины. Так как аксиома выполнена для евклидова отрезка , то она выполнена и для неевклидова отрезка AB.

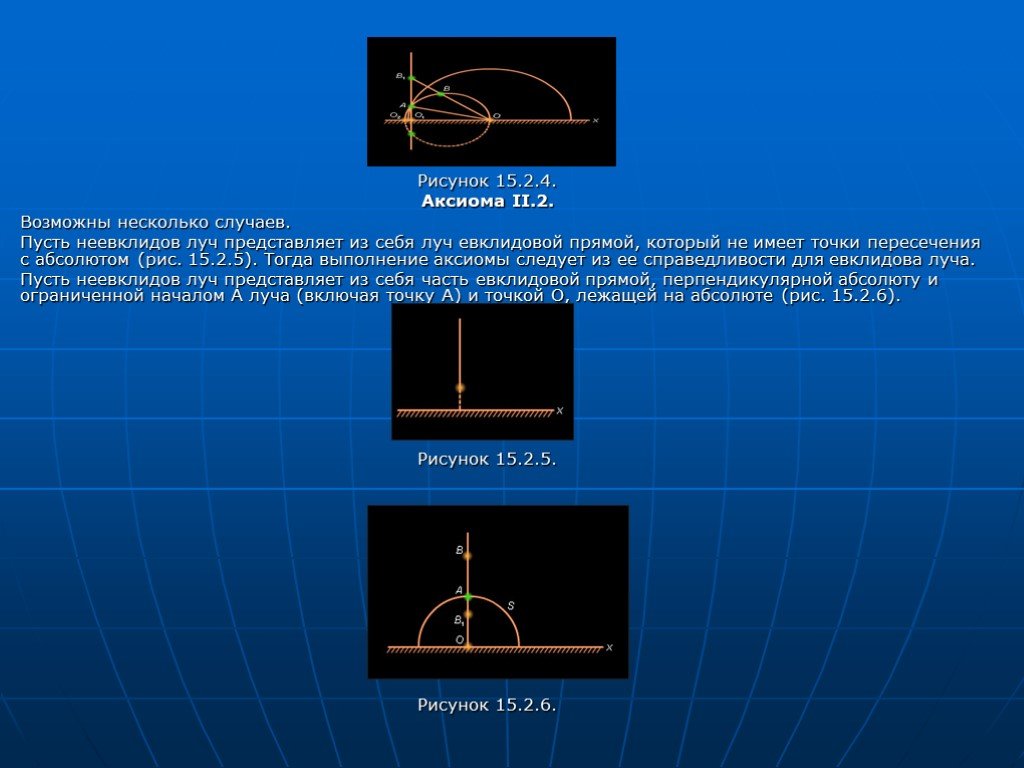
Рисунок 15.2.4. Аксиома II.2. Возможны несколько случаев. Пусть неевклидов луч представляет из себя луч евклидовой прямой, который не имеет точки пересечения с абсолютом (рис. 15.2.5). Тогда выполнение аксиомы следует из ее справедливости для евклидова луча. Пусть неевклидов луч представляет из себя часть евклидовой прямой, перпендикулярной абсолюту и ограниченной началом A луча (включая точку A) и точкой O, лежащей на абсолюте (рис. 15.2.6). Рисунок 15.2.5. Рисунок 15.2.6.

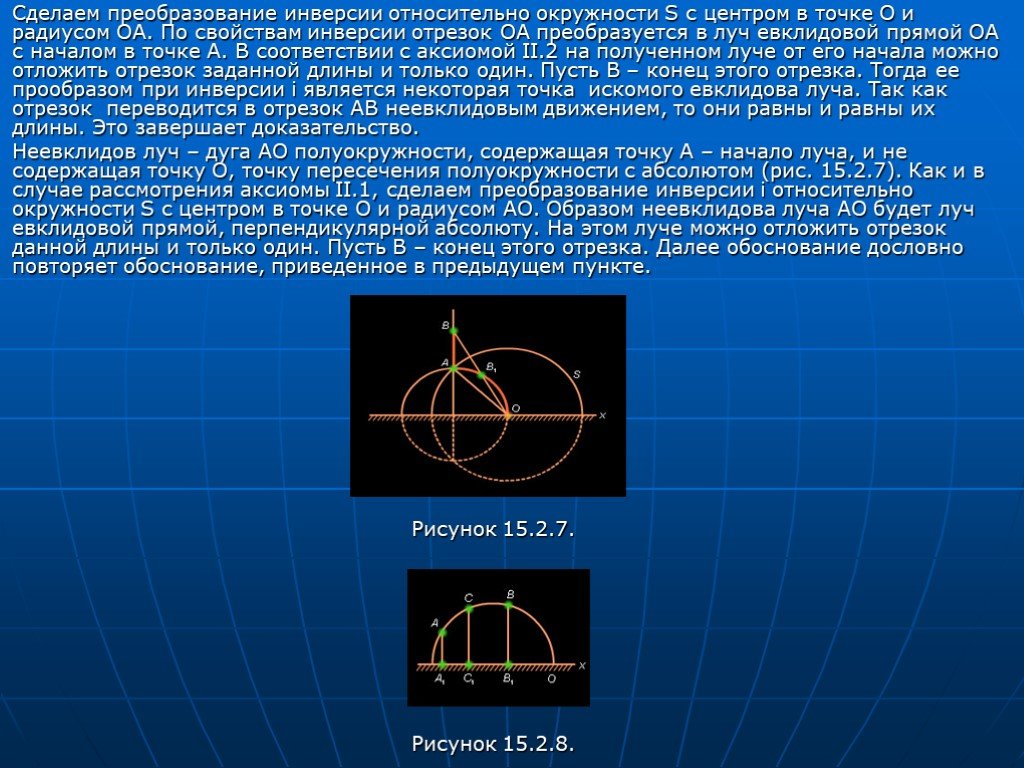
Сделаем преобразование инверсии относительно окружности S с центром в точке O и радиусом OA. По свойствам инверсии отрезок OA преобразуется в луч евклидовой прямой OA с началом в точке A. В соответствии с аксиомой II.2 на полученном луче от его начала можно отложить отрезок заданной длины и только один. Пусть B – конец этого отрезка. Тогда ее прообразом при инверсии i является некоторая точка искомого евклидова луча. Так как отрезок переводится в отрезок AB неевклидовым движением, то они равны и равны их длины. Это завершает доказательство. Неевклидов луч – дуга AO полуокружности, содержащая точку A – начало луча, и не содержащая точку O, точку пересечения полуокружности с абсолютом (рис. 15.2.7). Как и в случае рассмотрения аксиомы II.1, сделаем преобразование инверсии i относительно окружности S с центром в точке O и радиусом AO. Образом неевклидова луча AO будет луч евклидовой прямой, перпендикулярной абсолюту. На этом луче можно отложить отрезок данной длины и только один. Пусть B – конец этого отрезка. Далее обоснование дословно повторяет обоснование, приведенное в предыдущем пункте. Рисунок 15.2.7. Рисунок 15.2.8.

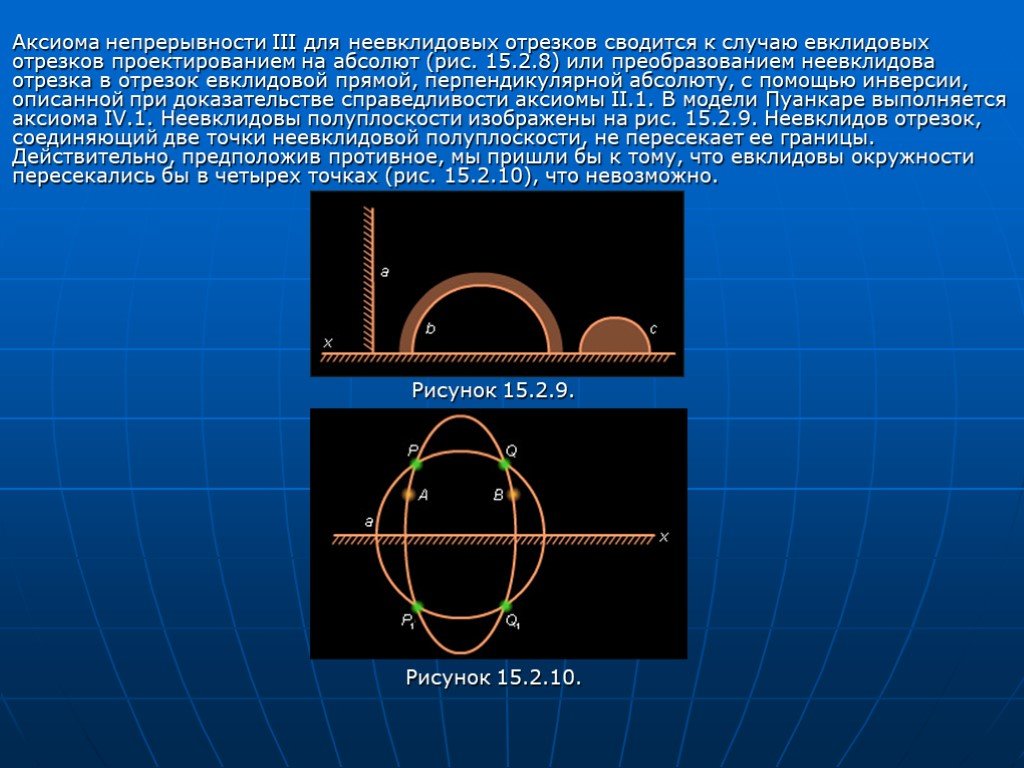
Аксиома непрерывности III для неевклидовых отрезков сводится к случаю евклидовых отрезков проектированием на абсолют (рис. 15.2.8) или преобразованием неевклидова отрезка в отрезок евклидовой прямой, перпендикулярной абсолюту, с помощью инверсии, описанной при доказательстве справедливости аксиомы II.1. В модели Пуанкаре выполняется аксиома IV.1. Неевклидовы полуплоскости изображены на рис. 15.2.9. Неевклидов отрезок, соединяющий две точки неевклидовой полуплоскости, не пересекает ее границы. Действительно, предположив противное, мы пришли бы к тому, что евклидовы окружности пересекались бы в четырех точках (рис. 15.2.10), что невозможно. Рисунок 15.2.9. Рисунок 15.2.10.

Аксиома IV.2. Возможные реализации углов в модели Пуанкаре для неевклидовых углов показаны на рис. 15.2.11. Рисунок 15.2.11. Рисунок 15.2.12. Из рисунка видно, что неевклидовыми углами являются угол между пересекающимися окружностями, а также между окружностью и пересекающей ее прямой. В соответствии с определением, данным в разделе 13, угол между пересекающимися окружностями это – угол между касательными к ним прямыми, проведенными в точке пересечения, а угол между окружностью и пересекающей ее прямой – это угол между касательной к окружности в точке пересечения и прямой. Таким образом величины неевклидовых углов определяются через величины соответствующих евклидовых углов. Отсюда достаточно очевидна справедливость аксиомы IV.2.

Аксиома IV.3. Пусть неевклидовым лучом является луч (или часть луча) евклидовой прямой, перпендикулярной абсолюту (рис. 15.2.12). В соответствии с аксиомой IV.3 отложим от луча в данную полуплоскость евклидов угол с заданной градусной мерой. Это можно сделать и единственным образом. Пусть p – другая сторона этого угла. Через вершину луча проведем прямую q, перпендикулярную к лучу p до пересечения с абсолютом в точке O. Такая точка существует и единственна. Проведем полуокружность с центром в точке O и радиусом OA. Такая окружность существует и единственна. В силу определения и построения угол между искомым неевклидовым лучом и построенной окружностью имеет данную градусную меру. Пусть неевклидовым лучом с вершиной A является часть AB полуокружности (рис. 15.2.13) с центром в точке O на абсолюте. Рисунок 15.2.13. Проведем касательную p к полуокружности в точке A и отложим от луча AC угол, равный данному, в полуплоскость, не содержащую данную полуокружность. Пусть q – вторая сторона угла. Восстановим перпендикуляр к лучу q в точке A. Если этот перпендикуляр пересекает абсолют в точке H, то, построив полуокружность с центром в точке H и радиусом, равным AH, получим две пересекающиеся в точке A полуокружности, угол между которыми равен α по построению. Если же перпендикуляр не пересекает абсолют, т. е. он параллелен абсолюту или, что то же самое, луч q перпендикулярен x, то второй стороной неевклидова луча является искомый

евклидов луч q. Единственность такого угла следует из справедливости аксиомы для евклидовой плоскости. Проверку аксиомы IV.4 проведем только для случая, когда данный неевклидов луч есть часть полуокружности. В соответствии с аксиомами II.2 и IV.3 отложим от вершины A данного луча отрезок равный данной стороне треугольника . Кроме того, отложим от данного луча в данную полуплоскость угол, равный углу A1 треугольника . На луче, задающем вторую сторону отложенного угла, отложим от точки A отрезок равный стороне исходного треугольника. Покажем, что полученный треугольник равен треугольнику Так как по построению равен , существует неевклидово движение f, переводящее отрезок в AB так, что При неевклидовом преобразовании углы сохраняются, поэтому либо точка окажется на луче , либо его можно совместить с точкой этого луча дополнительной осевой симметрией относительно луча . При этом по свойству 3 отрезок перейдет в себя и В силу свойства 1 преобразование также будет неевклидовым движением. Покажем, что точка C3 совпадет с C2. Действительно, если бы это было не так, то оказалось бы, что на луче AC2 отложены два различных отрезка данной длины, что противоречит аксиоме II.2. Следовательно, существует неевклидово движение, которое переводит данный треугольник в треугольник , что завершает доказательство. Утверждение аксиомы параллельности Лобачевского выполняется не только для некоторой прямой a и некоторой точки A, не лежащей на a, но и для любой неевклидовой прямой a и любой не лежащей на ней точки A (рис. 15.2.14). Рисунок 15.2.14.

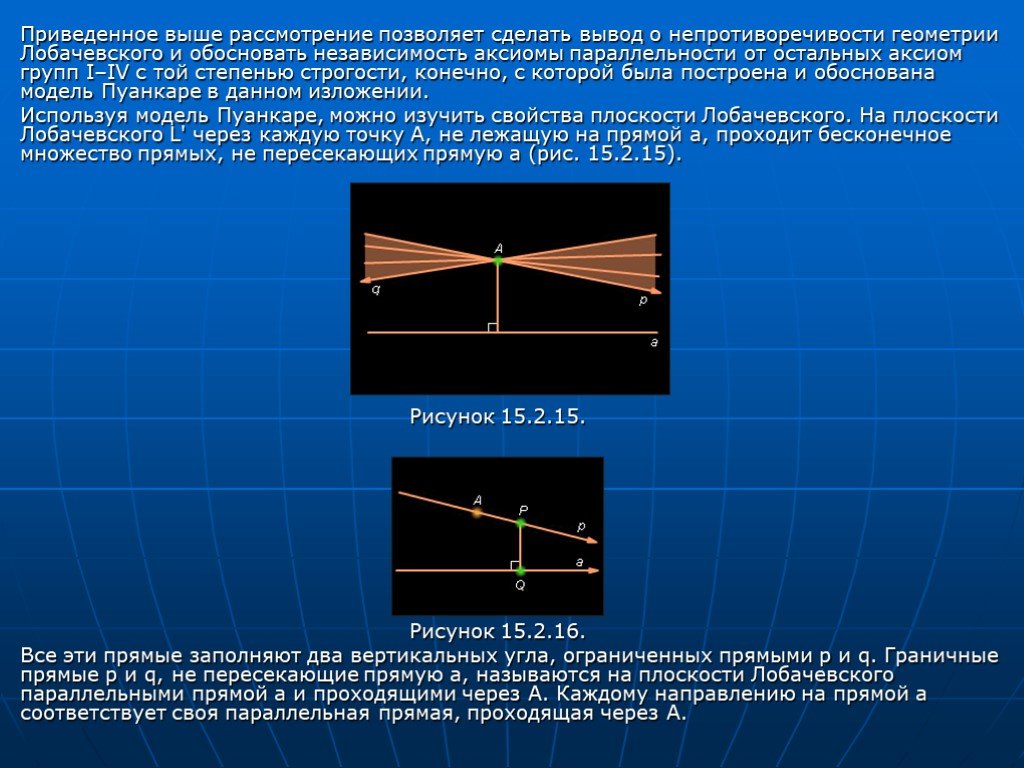
Приведенное выше рассмотрение позволяет сделать вывод о непротиворечивости геометрии Лобачевского и обосновать независимость аксиомы параллельности от остальных аксиом групп I–IV с той степенью строгости, конечно, с которой была построена и обоснована модель Пуанкаре в данном изложении. Используя модель Пуанкаре, можно изучить свойства плоскости Лобачевского. На плоскости Лобачевского L' через каждую точку A, не лежащую на прямой a, проходит бесконечное множество прямых, не пересекающих прямую a (рис. 15.2.15). Рисунок 15.2.15. Рисунок 15.2.16. Все эти прямые заполняют два вертикальных угла, ограниченных прямыми p и q. Граничные прямые p и q, не пересекающие прямую a, называются на плоскости Лобачевского параллельными прямой a и проходящими через A. Каждому направлению на прямой a соответствует своя параллельная прямая, проходящая через A.

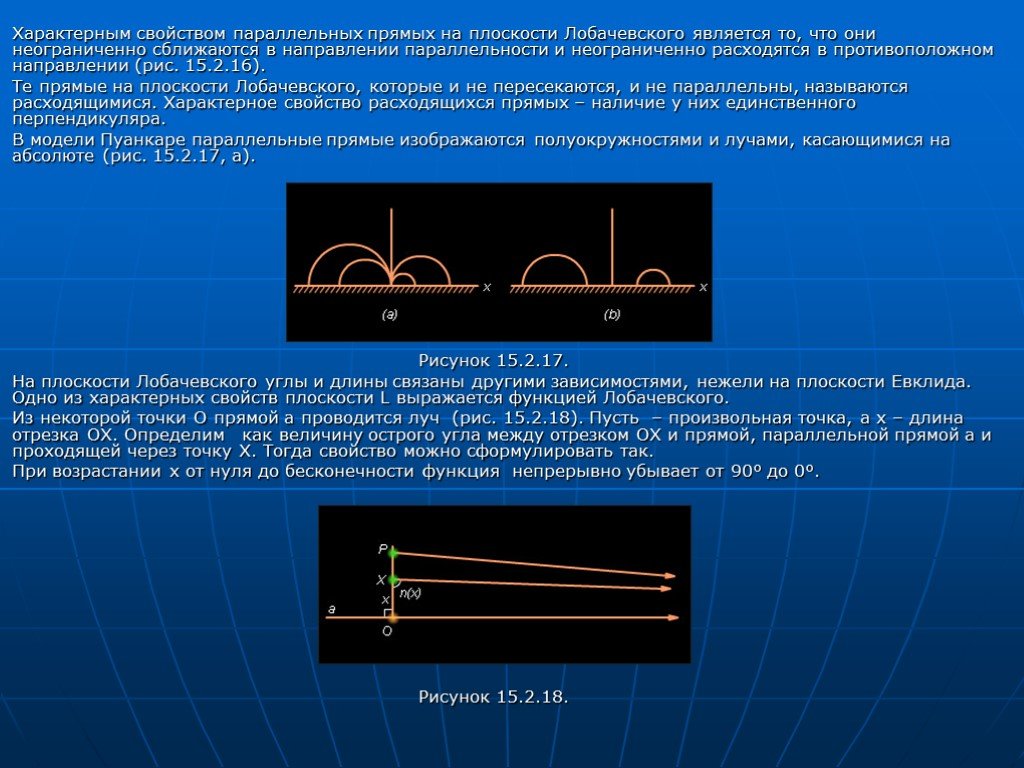
Характерным свойством параллельных прямых на плоскости Лобачевского является то, что они неограниченно сближаются в направлении параллельности и неограниченно расходятся в противоположном направлении (рис. 15.2.16). Те прямые на плоскости Лобачевского, которые и не пересекаются, и не параллельны, называются расходящимися. Характерное свойство расходящихся прямых – наличие у них единственного перпендикуляра. В модели Пуанкаре параллельные прямые изображаются полуокружностями и лучами, касающимися на абсолюте (рис. 15.2.17, а). Рисунок 15.2.17. На плоскости Лобачевского углы и длины связаны другими зависимостями, нежели на плоскости Евклида. Одно из характерных свойств плоскости L выражается функцией Лобачевского. Из некоторой точки O прямой a проводится луч (рис. 15.2.18). Пусть – произвольная точка, а x – длина отрезка OX. Определим как величину острого угла между отрезком OX и прямой, параллельной прямой a и проходящей через точку X. Тогда свойство можно сформулировать так. При возрастании x от нуля до бесконечности функция непрерывно убывает от 90° до 0°. Рисунок 15.2.18.

Существование таких зависимостей между длинами отрезков и углами означает, что на плоскости Лобачевского нет подобных фигур. Например, на плоскости Лобачевского справедлив признак равенства треугольников: если углы одного треугольника соответственно равны углам другого треугольника, то такие треугольники равны. Сумма углов треугольника на плоскости Лобачевского меньше 180°. Разность между 180° и суммой углов треугольника называется избытком треугольника. Оказывается, что на плоскости Лобачевского площадь треугольника пропорциональна его избытку. Следовательно, на плоскости Лобачевского площади треугольников ограничены некоторой постоянной. Величины углов на плоскости Лобачевского в модели Пуанкаре равны величинам соответствующих углов на евклидовой плоскости. Поэтому все перечисленные свойства углов плоскости L можно увидеть на модели Пуанкаре. Для иллюстрации аксиомы о параллельности прямых рассмотрим следующую схему. Имея прямую a и точку A вне ее, соединяем A с точкой P, лежащей на a, и отодвигаем точку P в положение P', P'', ... и все дальше, и дальше на a (иными словами, представляется последовательность точек P, P', P'', ... или соответственно последовательность прямых AP, AP', AP'', ...). Прямая AP при этом вращается вокруг A и достигнет некоторого предельного положения, когда P удалится в бесконечность, и эту предельную прямую и надо понимать как прямую, параллельную прямой a, проходящую через A. При этом нет никаких изначальных соображений, в силу которых прямая AP должна приближаться к одному и тому же предельному положению при удалении P в бесконечность как в одну, так и в другую сторону, что дает абстрактную возможность существования двух различных прямых, проходящих через A, параллельных прямой a. В этой связи постулат параллельных прямых в евклидовой геометрии – не что иное, как соглашение о том, что эти два предельных положения должны совпадать, и через точку A должна проходить только одна прямая, параллельная прямой a. На примере геометрии Лобачевского было показано, что допущение о несовпадении

предельных прямых, а именно отрицание аксиомы о единственности прямой, проходящей через точку A, не привело к противоречию, а наоборот, привело к построению новой неевклидовой геометрии. Однако наряду с геометрией Лобачевского существует еще один вид неевклидовой геометрии, которую полезно упомянуть.