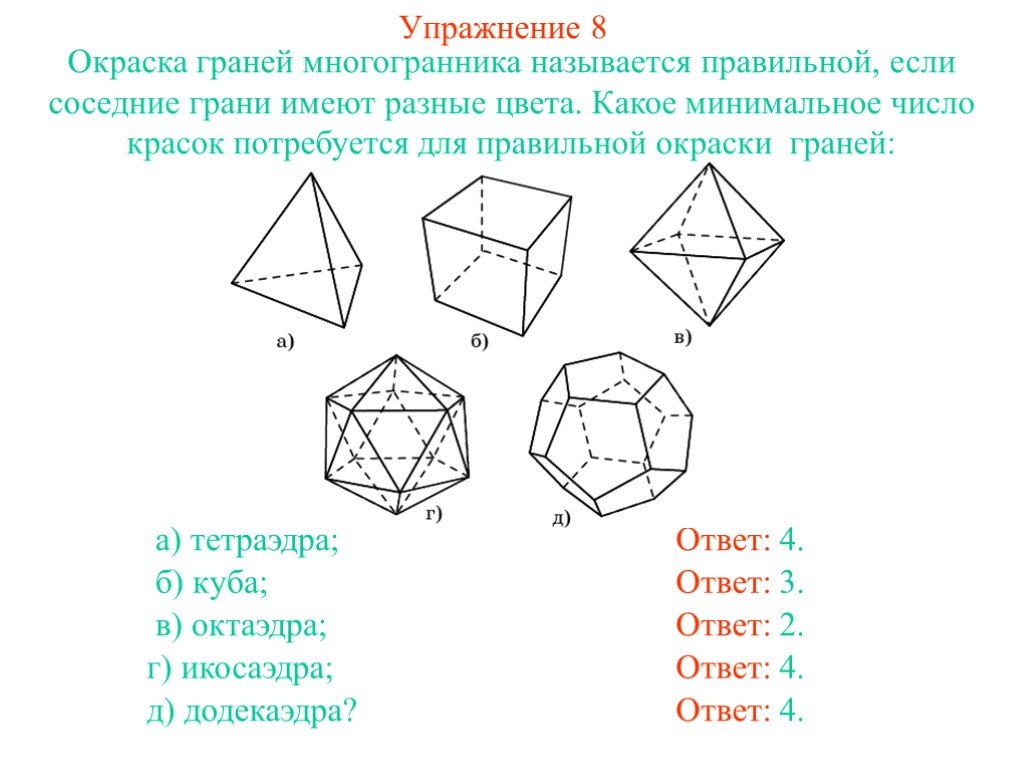
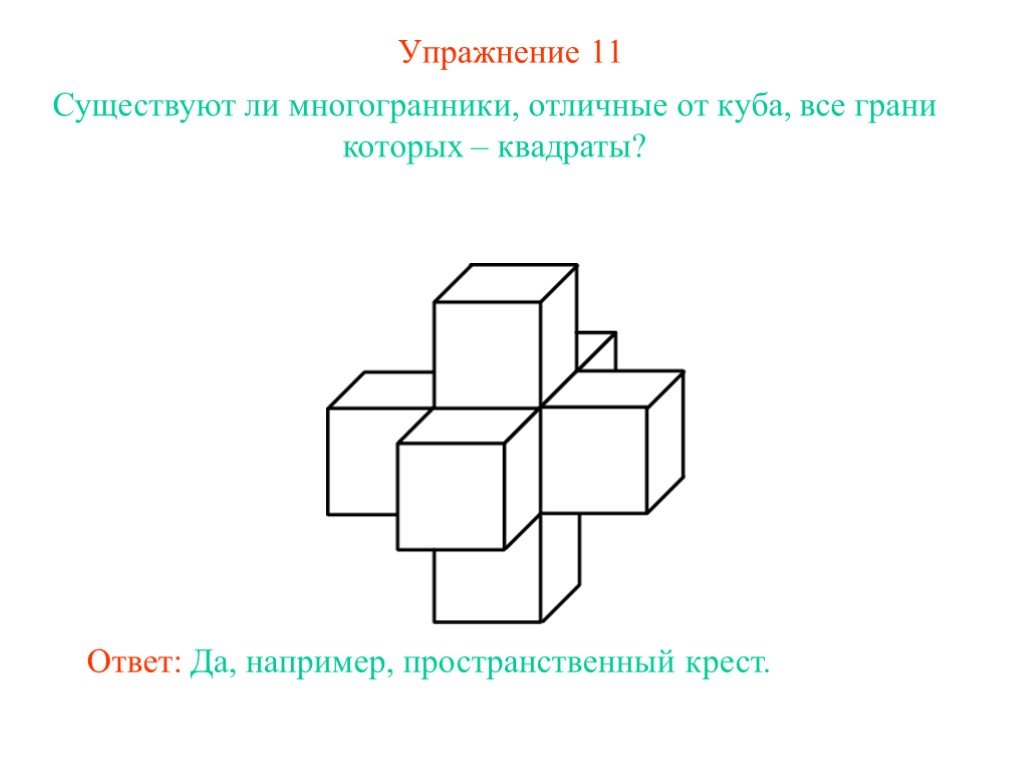
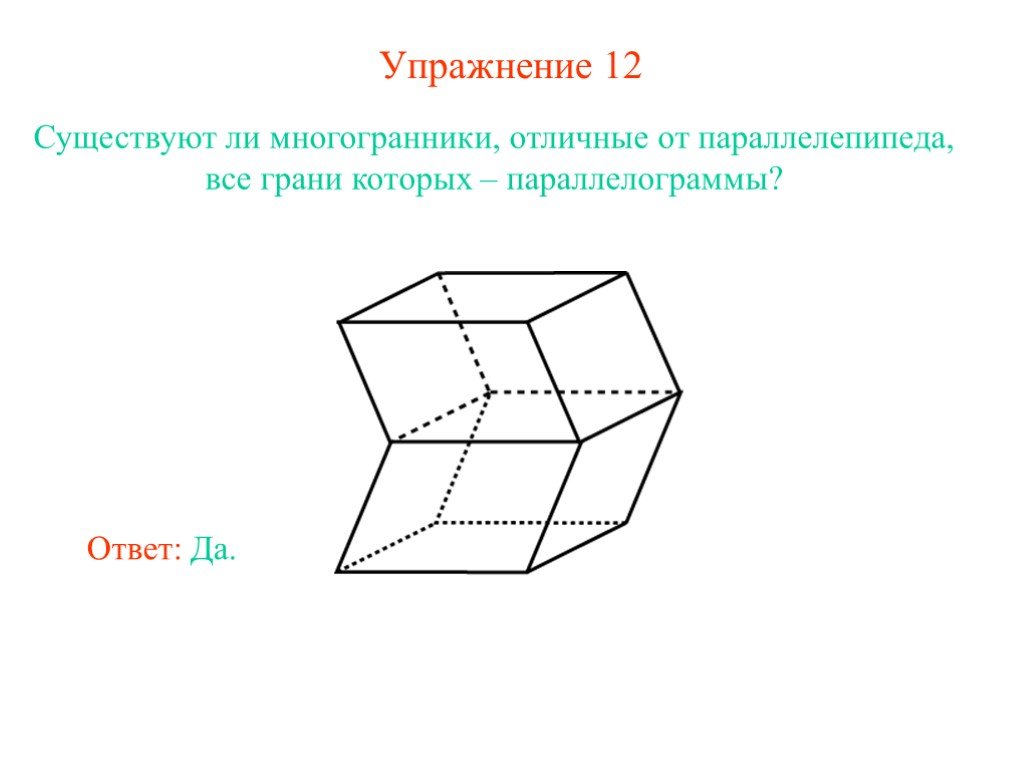
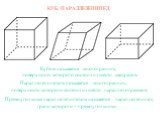
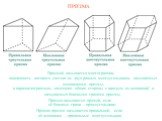
Презентация "Куб, параллелепипед" по математике – проект, доклад
Презентацию на тему "Куб, параллелепипед" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
Куб и прямоугольный параллелепипед
Цели урока: - Сформировать знания, умения и навыки построения прямоугольного параллелепипеда и куба. - Научить учащихся применять и использовать формулы ...Прямоугольный параллелепипед. Куб
А В С D А1 В1 С1 D1. Прямоугольный параллелепипед, куб. К Х У Х1 У1 К1. Х,Х1 – вершины (8) ХК,КК1- рёбра (12) ХХ1К1К, ХХ1У1-грани (6). a b c V= abc ...Прямоугольный параллелепипед и его свойства
Прямоугольный параллелепипед. Цель урока:.познакомиться с понятием прямоугольный параллелепипед, его составными частями, их свойствами, нахождением ...
Задачи на прямоугольный параллелепипед
Итоговый урок в 5 классе по теме: «Прямоугольный параллелепипед и куб». «Урок – путешествие в страну стереометрию» Цели: проверка умений построения ...Прямоугольный параллелепипед
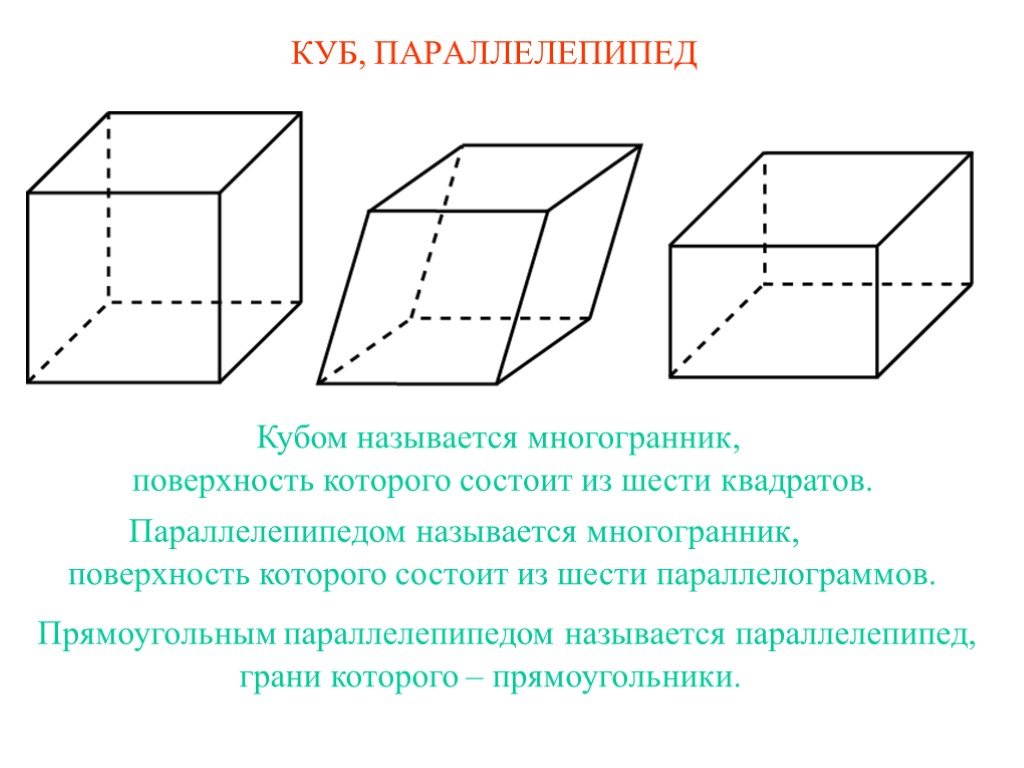
Параллелепипед. Параллелепипед – шестигранник, все грани которого (основания) – параллелограммы. Параллелепипед имеет 8 вершин и 12 рёбер. Грани параллелепипеда, ...Прямоугольный параллелепипед
Прямоугольный параллелепипед - это тело, все грани которого - прямоугольники. Параллелос в переводе с древнегреческого буквально означает «идущие ...Прямоугольный параллелепипед
. . Решите задания и заполните таблицу. Найдите площадь квадрата, сторона которого равна 9 см. (П) Найдите площадь прямоугольника со сторонами 6 см ...Прямоугольный параллелепипед
Примеры предметов, имеющих форму прямоугольного параллелепипеда. Аквариум имеет форму прямоугольного параллелепипеда. Его боковые стенки – стеклянные. ...Математика прямоугольный параллелепипед
А В С D1 С1 Вершины - точки. Грани - прямоугольники. Ребра - отрезки А1 D В1. Какие предметы имеют форму прямоугольного параллелепипеда? a c V=abc ...Прямоугольный параллелепипед
Цель урока:. -познакомиться с прямоугольным параллелепипедом, кубом, их элементами; -научиться чертить эти фигуры; - находить длину ребёр и S поверхности. ...Куб и его свойства
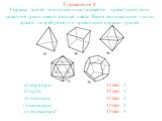
ГДЕ НАЧАЛО КУБА? Цель работы: Выяснить какие секреты хранит куб? Задачи: Во время исследования куба обнаружить некоторые его свойства Научиться самостоятельно ...Тетраэдр и параллелепипед
Свойства параллелепипеда. 1.Противоположные грани параллельны и равны. Диагонали пересекаются и делятся точкой пересечения пополам. С В А D А1 В 1 ...Куб и его свойства
Цели урока. • Личностные: уважение к личности и ее достоинству, устойчивый познавательный интерес, умение вести диалог на основе равноправных ...Куб 5-6 класс
Проверка домашнего задания:. Вылепить из пластилина куб, с ребром 2,5 см. 1. У куба 10 вершин? Ответьте на следующие вопросы, используя Ваш куб:. ...Куб
Куб – это правильный многогранник, каждая грань которого представляет собой квадрат. Куб имеет: Объем куба: 6 граней V= a*a*a=a3 8 вершин Площадь ...Куб
? Сходства и отличия. Сходства и отличия квадрата и куба. . Куб — геометрическая фигура, каждая грань которого представляет собой квадрат. Из словаря:. ...Куб
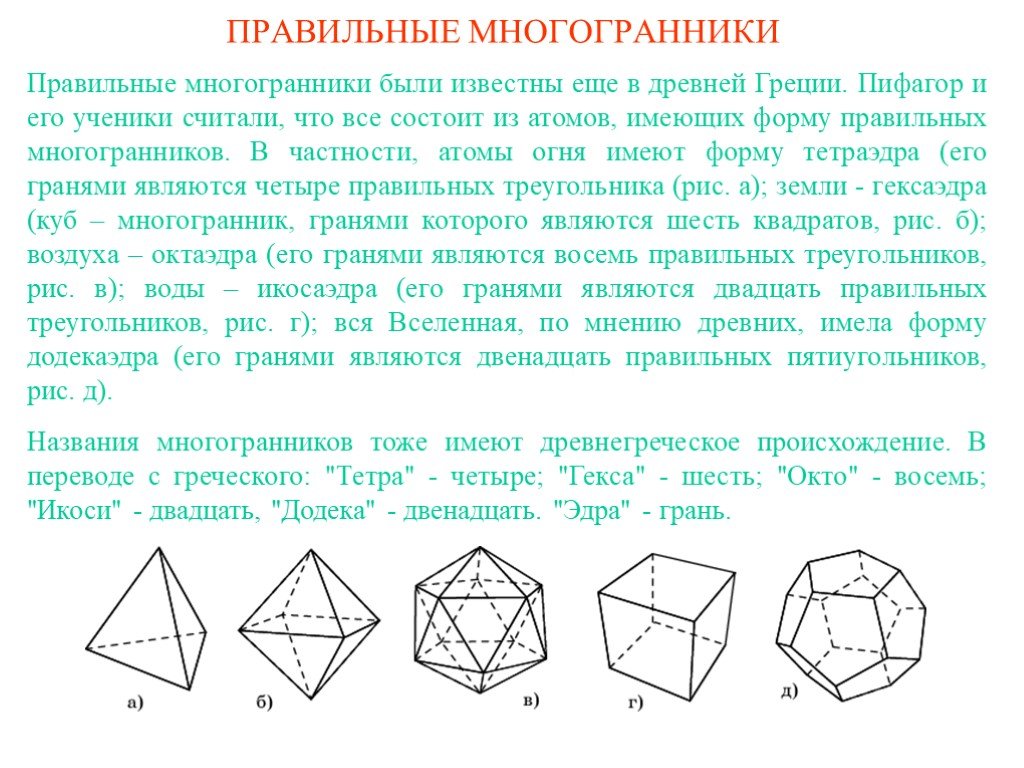
КУБ (ГЕКСАЭДР). Куб или гексаэдр – представитель правильных выпуклых многогранников. Куб имеет шесть квадратных граней, сходящихся в каждой вершине ...Возведение в степень. Куб и квадрат числа
Устно. Упростить выражение: 25х + 15 х; 12у – 3у; 9k + 9k – 4k; 80c-35c-14c; 8d+d-9d; 163 + 37v + 18v. Решить уравнение: 7х+2х = 918; 5а-3а = 222; ...Простейшая геометрия
Задача 1. Ремонт водителям не помеха. На участке дороги идет ремонт. Водителям приходится объезжать этот участок по запасному пути, отмеченному на ...Смежные и вертикальные углы геометрия
Цели урока:. Познакомить учащихся с понятиями смежных и вертикальных углов. Научить строить угол, смежный с данным. Научить строить вертикальные углы. ...Конспекты
Параллелепипед. Куб
Технологическая карта урока математики в 4 классе. УМК «Начальная школа 21 века». Тема урока:. Параллелепипед. Куб. Тип:. изучение нового материала. ...Прямоугольный параллелепипед и куб. Куб числа
Математика 3 класс. Тема: «Прямоугольный параллелепипед и куб. Куб числа". Цели: 1. Дать представление о прямоугольном параллелепипеде и кубе, ...Куб, как частный случай прямоугольного параллелепипеда
Конспект урока математики. 9 класс. Тема: «Куб, как частный случай прямоугольного параллелепипеда». Автор: Старикова Галина Владимировна, учитель ...Прямоугольный параллелепипед
Тема урока:. «Прямоугольный параллелепипед». . . Цели:. . ввести понятие прямоугольного параллелепипеда; показать правила изображения в тетради ...Прямоугольный параллелепипед
Муниципальное общеобразовательное бюджетное учреждение. средняя общеобразовательная школа№5 г. Благовещенска. Республики Башкортостан. ...Прямоугольный параллелепипед
МОУ Белоомутская средняя общеобразовательная школа №1. УРОК. ПО ТЕМЕ :. ГЕОМЕТРИЯ 10 КЛАСС. Учитель: ПАРФЕНОВА В.А. ...Прямоугольный параллелепипед
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа №2 г.Турана. Разработка ...Прямоугольный параллелепипед
Муниципальное общеобразовательное учреждение. . «Средняя общеобразовательная школа № 3 г. Козьмодемьянска». . Республики Марий Эл. ...Куб и конструкции из кубиков
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ. СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 67. С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ ОТДЕЛЬНЫХ ПРЕДМЕТОВ. ...Прямоугольный параллелепипед
Конспект урока математики в 5 классе по теме. «Прямоугольный параллелепипед». Автор:. Смирнова Лариса Владимировна, учитель МОУ Большекошинской ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 марта 2019
Категория:Математика
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию